卷积（背后意义、应用及计算）

一、卷积及其背后的意义

卷积的意义在于：在上一节中，我们讨论了傅里叶变换，其目的在于将一个函数分解为若干个不同频率的正弦波组成。那么，为何要将一个完整的函数分解为正弦波呢？这是因为这样做可以简化计算过程。正弦函数在求导和积分后，其结果依然是正弦函数，同时，许多在时域难以处理的问题，在频域中却变得简单易解，例如噪声滤波。下面提供了傅里叶变换的讲解链接，有兴趣的朋友不妨一观。

opencv

然而，将信号转换为正弦波形态有时也难以处理，这时我们还需将某一函数转化为其他形态，例如冲激函数，从而产生了卷积这一概念。因此，卷积实际上与傅里叶变换类似，都是一种函数转换的手段，不过它们转换函数的方式不同。傅里叶变换将原始函数分解为一系列不同频率的正弦波，而卷积则将函数转化为一系列冲激函数。至于将函数转换为冲激函数的用途，将在第二部分通过具体实例进行阐述。

2、卷积是如何将一个函数拆分成一个个的冲激的

（1）阶跃函数

首先这里需要引入一个阶跃函数

开元棋官方正版下载，其表达形式如图1所示：

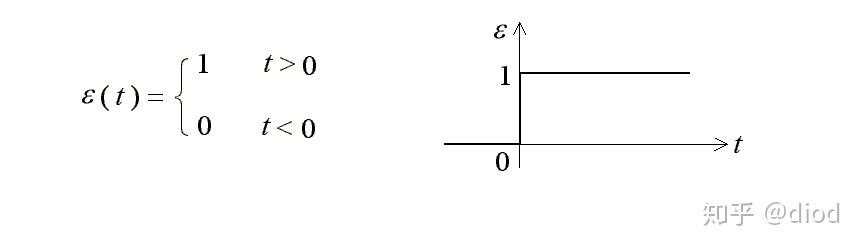
图1

我们可以通过这个函数将原函数分成一段一段的，具体操作如下：

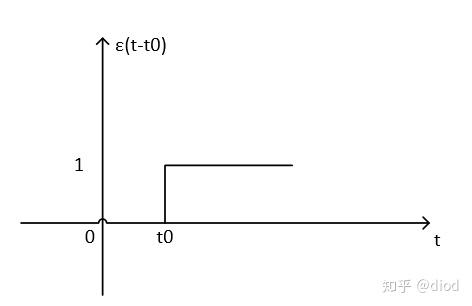
图2

将上述函数向右平移一段距离，即可观察到图2所展示的图形。若要将原始函数分割成若干个连续的小段落，每个段落长度设为t0，那么只需设定

即可，即得到

这一特定位置上的一个变体，通过调整n的数值开yun体育官网入口登录app，这个小段可以随意改变其在整体中的位置，进而与原函数相乘，从而获得原函数在指定点的相应变化形式。

该函数的近似值。由此，我们可以推导出以下公式，尽管它颇为冗长，却相当直观，即通过将原始函数分割成众多小部分并逐一累加。

在将原函数划分为无数个点所构成的结构时，原函数便能够被表达为以下这种形态。

我们将

单独提出来分析，当

时这是一个求导的式子，求的是函数

处的导数，从图1、图2我们知道，函数

处发生了跳变，对这点的求导需要引入一个新的函数即冲激函数

（2）冲激函数

定义：

图像：

为什么冲激函数是函数

那处的导数，相当于无穷大的力量（即突变），但其作用仅限于极短的时间（仅在t=0时刻），因此仅产生了有限的影响（即阶跃至1）。这种影响，实际上是对无穷大与无穷小相乘后取极限的结果。

3、有了上述铺垫，现在我们再回到这个公式

可以将上述式子写成一下形式

时，每次n增加对

的影响非常小，因此

可以看作是一个连续变化的值，将其看作连续量

，则上式可以写成如下形式：

如此一来，原函数便被成功分解为一系列冲激的构成，而上述的原理同样可以参照珂学原理的相关文档进行学习。

链接如下：

如何用δ(t)表示任意的连续时间信号（函数）

二、卷积的应用

在接听电话的过程中，现代智能手机会自动执行降噪操作，这一功能是通过卷积技术来实现的。

在通话过程中，四周充斥着各种杂音，然而对方却无法察觉到我们这边的噪音。这是因为手机对传入的声波进行了处理，提升了我们的声音，同时滤除了干扰。这样的情形我们再熟悉不过，自然而然地，我们会联想到傅里叶变换。然而，想象一下，世界上有如此众多的声音，如此繁复的组合，每个人都是独一无二的，他们又可以相互组合。声波的形态千变万化，其频率组合同样种类繁多。我们无法对世界上所有的人进行取样，以分离出每个人的声音。但所有函数波形都可以分解为一系列的冲激。对于每一个冲激输入，我们赋予它一个相应的输出。这样一来，问题就变得简单了许多。我们的任务就是让系统对冲激产生一个固定的响应。

对应的过程如下图所示（图片来在珂学原理）：

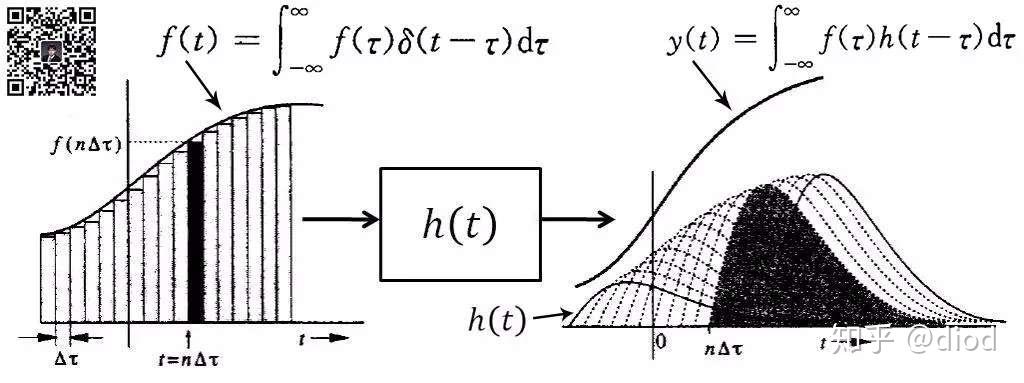
每个单位冲激都对应着h(t)，这构成了一个线性时不变系统。无论何时输入冲激开元ky888棋牌官方版，其响应始终保持一致。因此，当冲激发生平移时，其响应函数也随之平移。而且，响应的幅度变化与冲激的幅度变化保持一致（若冲激幅度增加，响应的各个位置也会按比例增大），正如上图所展示的那样。每个冲激都对应一个h(t)的波形，这个波形会随着冲激的移动而移动，并随着冲激幅度的变化而同比例变化。最终，每个时刻的值都是这些响应在该时刻的累积和。最终形成的新的波形就是一个经过滤噪之后的目标波形。

三、卷积的计算

1、数学计算，代入求的时刻t然后积分就好

2、卷积的数学意义

公式：

（注意：

是变量）

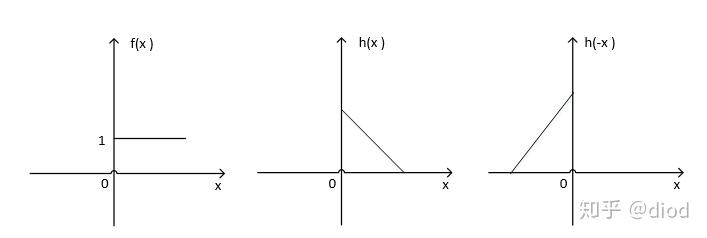
对于

图像相当于将

先沿着y轴对称翻转，然后再向右移动

个单位

因此

就相当于翻转后又向右平移了

个单位长度，因此改变t就相当于在不断的平移翻转后的

函数，在函数

和函数

相交的部分对应相乘并求和。

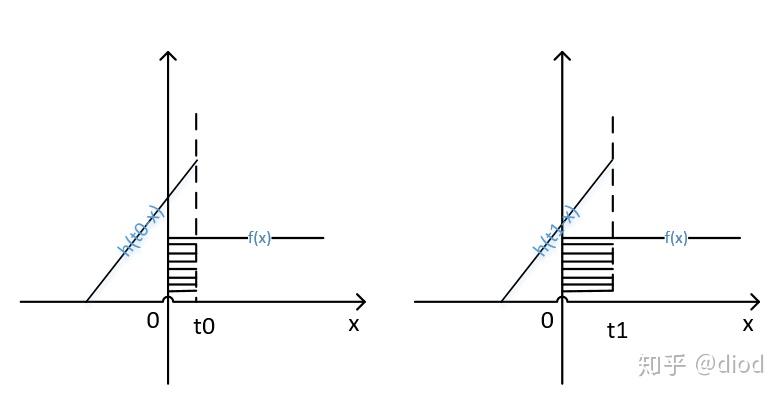
用下面一组图来说明：图片中的x均相当于上述公式中的

，卷积每次求解的就是阴影部分的面积

推荐一本很好的opencv入门书籍