蜂群遗传算法在一维下料问题中的应用
摘要: 针对一维切割优化难题,结合企业具体的生产条件,对满足与不满足生产需求两种情形进行考量,构建了一个全新的优化模型。该模型采用蜂群遗传算法来寻找解决方案。以各零件的长度顺序构成染色体,将每个零件的尺寸视为染色体的基因。依据蜂群行为特点,设定了两个种群,其中种群1负责全局范围内的搜索,而种群2则专注于局部区域的探索。实验结果表明,该模型具有一定的实用价值。
针对一维下料问题,我们采用了一种优化下料的方法,该方法基于蜂群遗传算法。在算法中,染色体和种群是核心概念,而抑制算子则用于控制算法的搜索过程。
将库存中的原材料进行切割开元ky888棋牌官网版,形成各种形状、尺寸不一或长度不同的零部件,以适应客户的具体需求,这一过程在钢铁、造纸、纺织和木材加工等行业中被普遍采用。Dyckhoff与Wascher对下料问题进行了详尽的分类。依据原材料的种类和零件的尺寸数量,下料问题可分为一维、二维和多维三个类别。
一维下料作为关键环节,构成了研究二维、三维等多维下料问题的基础。针对这一问题,不同学者聚焦于不同的研究方向,比如力求最大程度地节省原材料、提升原材料的使用效率;探讨如何降低排样方案的数量;优先采用较短的原料,并适当增加最后一根余料的长度;确保在既定的交货期限内完成生产任务等。研究发现,众多探讨一维下料问题的研究文献往往忽略了企业生产力短缺的实际情况,导致企业在这种情况下可能遭受损失或盈利减少。部分文献对存在交货期限限制的一维下料问题进行了探讨,通过合理规划生产流程来降低因延迟带来的损失;尽管某些文献对不完全下料问题提出了应对策略,但研究主要集中在如何提升原材料利用率上,而涉及此问题的其他文章则相对较少。企业的生产能力在任何时候都存在局限,这既包括加工制造的能力,也包括原材料的储备。不同零件的市场价值以及后期加工的紧迫性,导致其带来的收益各异。当企业遭遇突发状况,必须面对时,决策者需考虑的一个关键问题是,如何合理规划生产,优先生产价值高、需求急迫的零件,同时尽量减少废料,以将企业损失降至最低。在此背景下,本文提出了一种基于价值导向、实际量化的新模型,专门针对单一规格原材料的一维下料问题。
1 模型结构
构建模型时需兼顾两大关键问题:首先,需确保企业自身具备满足生产需求的能力,这包括具备充足的生产能力和原材料库存。在此背景下,决策者尤为关注下料方案产生的废料最少、原材料利用率最高等问题,此时模型的核心任务便是如何最大限度地利用原材料。其次,还需考虑因客观因素导致的生产力受限或上游原材料供应不足,进而影响按时完成生产任务的情况。在这种情况下,优先安排生产那些需求紧急且延迟交货损失价值高的零件,以保障企业整体损失降至最低。
参数设定具体如下:企业需生产m种不同零件,其中i代表待生产零件的序号;li表示第i种零件的尺寸长度;vi是该零件在市场上的价值;di是第i种零件的需求量;L代表原材料的总长度;v是原材料的单价;n是生产过程中所需原材料的总量;aij表示使用j号原材料生产的第i种零件的数量;cj是j号原材料切割后剩余的废料长度;E则是企业的生产能效或原材料供应的限制。具体模型如下:

目标函数(1)旨在实现企业整体损失的最小化,在生产过程中,其目标转变为降低生产完成后废料的损失;式(2)保障企业生产量不超需求量,实现供需平衡,并认为超量生产的零部件将引发库存积压、管理成本和损耗等额外费用,这些同样被视为损失;式(3)确保在单根原材料上生产的零部件总长度不超过原材料长度,否则生产活动将无法进行;式(4)对企业的实际生产零件数量进行限制。
2 蜂群遗传算法
依据前述构建的模型,我们运用了广泛应用的遗传算法来解决问题。这一算法最初由美国密歇根大学的Holland教授及其研究生在20世纪60年代末至70年代初提出。在本文中,我们采纳了一种基于蜂群繁殖机制的改进版遗传算法,该算法不仅确保了最优个体的生存和繁殖资格,同时也维护了种群内个体的多样性。
在自然界,一个蜂群由蜂后、雄蜂和雌蜂三个群体构成,其中每个蜂群仅存在一位蜂后,她独享着繁殖的特权。若蜂后不幸离世或丧失了繁殖能力,众多具备成为蜂后潜力的雌蜂便会展开激烈的竞争,直至其中一位脱颖而出,接替蜂后的位置。蜂后能够孕育出两种不同的幼虫,其中一类将成长为雌蜂,数量上占据多数,但她们不具备繁殖的能力;另一类则会成长为雄蜂,数量相对较少,其主要职责是与蜂后完成交配任务。
依据蜜蜂繁殖的法则,文中所述的蜂群遗传算法中,其种群由蜂王、雄蜂群体与雌蜂群体这三部分构成,具体来说,蜂王仅有一位,而雄蜂群体的成员数达到N,雌蜂群体的成员数则为M。
2.1 适应度函数
文中阐述的一维切割问题,其优化追求的是使切割方案的综合损耗降至最低。在评估算法的适应度函数时,通常认为适应度值越高,所得到的解的品质越优良。基于这一考虑,本研究选取的适应度函数为:
分子代表的是已制成零件的价值总额,减去废料价值后的总和;分母则是满足总需求的零件价值总和。只有在需求得到完全满足且无多余零件的情况下,适应度函数的数值方能达到最高,即达到1,这也就意味着原材料的利用率达到了百分之百。
2.2 染色体编码
基因表达的形式亦称作编码方式,在种群中,每一个生物体开yunapp体育官网入口下载手机版,亦即每一根染色体,都是由基因所组成。在本研究中,我们采用了一种零件的全面排列组合的编码方法,具体来说,个体内的每一个基因都对应着一种零件。比如,一个由1个3号零件、2个2号零件、1个8号零件以及3个5号零件随机组合而成的编号序列(2,5,3,8,2,5,5)便代表了一个特定的个体。在解码过程中,选取一种原材料,依照编号顺序挑选相应部件进行切割,直至该原料无法再与所选部件相匹配,随后将已切割部件的编号从序列中移除,接着取用另一原材料,对剩余的编号序列重复上述操作,直至生产需求得到满足或原材料耗尽。
2.3 遗传算子的选择
2.3.1 交叉算子
蜂群通过交叉配对的方式,依据交叉率和蜂后的特点进行操作,这样做有助于培育出适应能力更强的个体。经过交叉,会诞生一雄一雌的后代。雄性后代将替代上一代,而雌性后代则暂时保存,以备后续处理。雄蜂群的存在主要是为了维持较高的选择压力,从而加快收敛的速度。交叉作为关键的遗传操作手段,在本文的设计中,我们采纳了顺序交叉的策略。具体操作是,先随机设定两个交叉点,接着交换这两个位置之间的基因片段。随后,从第二个交叉点开始,在原始的父代个体中,移除由另一父代个体所交换的基因。最后,从第二个交叉点之后,填补剩余的基因,以此方式生成两个全新的染色体。
2.3.2 变异算子
变异现象能够引入种群中原本不存在的染色体,从而丰富了种群的信息内容。在变异算子的设计上,通常会选择多点交换的方式进行变异。具体到本文,所采用的变异算子是两点变异,这意味着在每条染色体上,以概率P随机挑选两个点进行交换操作。变异发生的几率决定了新基因在种群中的占比,若此几率过低,那么有益的基因便难以被选择所采纳;反之,若变异几率过高,则可能导致后代丧失了由双亲遗传而来的优良特性。
2.3.3 选择算子
蜂群采用锦标赛式的选拔机制,对杂交产生的雌性幼虫与原蜂群中的成员进行挑选,进而构建由M个成员组成的新雌蜂群体。此选拔过程涉及:从两个群体中各自随机选取x个成员进行对比,选取适应度较高的个体予以保留,直至达到新群体的既定规模。该新蜂群中的雌蜂与旧蜂群中的雌蜂在个体特征上显现出不少区别,因此必须重新挑选蜂后。挑选方式为从新蜂群中挑选出适应性最强的个体,并与现任蜂后进行对比。若新选蜂后的适应性超越现任蜂后,则可替换现任蜂后;若不然开yun体育app入口登录,现任蜂后将保持不变。通常情况下,选拔锦标赛的规模设定为两人。
2.3.4 抑制算子
蜂后为了巩固其统治地位,必须对那些编码相似度较高的染色体实施抑制,这一抑制的临界值设定为T。其具体的抑制操作如下:一旦发现雌蜂群体中存在与蜂后之间的欧式距离D不超过T的个体,便对这些个体实施抑制,将其删除并替换为随机选取的个体。而对于那些未受抑制的个体,则按照既定的变异率进行变异。雌蜂群体的主要目标在于维护物种的遗传多样性,以防止种群过早地趋于稳定,确保能够随时突破局部最优解。其中,欧式距离D的计算公式如下:
在此,参数d代表染色体的整体长度,而Abi指的是A染色体上的第i个基因位点,Bbi则是指B染色体上的第i个基因位点。
2.3.5 算法描述
蜂群遗传算法,简称BSGA(Bee-Swarm Genetic Algorithm),其运作流程的阐述如下:
随机划分出两个群体,即雄蜂群与雌蜂群,每个群体分别包含N个和M个成员,然后从雌蜂群中挑选出适应能力最强的个体担任蜂后的角色。
雄性个体经过轮盘选择过程,按照既定的交叉比例与蜂后交配,从而孕育出一对雄性和雌性后代,随后对这些后代实施变异操作。
蜂群采用锦标赛式的选拔方式,对新生雌性幼虫与原有雌性成员进行挑选,进而将这些个体重新组合,形成由M个成员构成的新雌蜂群体。
对新形成的雌性群体实施蜂群后排挤策略,对那些与蜂后保持欧式距离D在特定界限内的个体进行淘汰,随后随机产生新的雌性个体,以填补因淘汰而减少的种群数量。
若算法的预设条件未能得到满足,则需返回至步骤(3)进行操作;若条件得以满足,则蜂后将被视为当前的全局最优解并输出。
(6)算法结束。
3 仿真案例分析
该仿真程序以PB语言进行编写,其中雄性个体数量设定为50,雌性个体数量同样设定为50,染色体交叉的成功率设定为80%,变异率设定为0.005,迭代过程的最大次数限制为100次。
算例1:计算参考文献中的例子。目前需要40段网线,其长度分别为4米、6米、10米、13米、14米、19米、20米、21米、22米、28米、32米、33米、36米、38米、38米、40米、41米、42米、48米、48米、50米、55米、57米、60米、64米、66米、67米、72米、76米、77米、83米、84米、85米、86米、91米、91米、94米、94米、99米、100米,需计算每箱305米长度的网线所需箱数及相应的分割方法。鉴于本文涉及的目标函数与适应度函数中包含了权重系数,因此对零件及原料设定了每米等值的单位成本为1,具体的价值与长度差异将在算例2中进行详细阐述。
表1展示了运用本篇文章提出的算法所计算出的数据,结果显示,在布线过程中,共需使用7箱网线,累计剩余材料长度为31米。在这31米的余料中,除去最长的一箱,其长度同样为31米,整体材料利用率达到了89.84%,而其他箱子的材料均得到了充分的利用。

模型主要针对的是在无法完成全部生产任务时的情况,探讨如何在有限的资源中实现价值最大化是本文的核心关注点。以下为算例2:假设需要生产10种不同长度的零件,其尺寸依次为135厘米、31厘米、23厘米、92厘米、28厘米、257厘米、14厘米、110厘米、55厘米和147厘米,对应的需求量分别是75个、250个、250个、45个、200个、50个、920个、67个、100个和15个。这些零件的价值分别为217元、44元、30元、113元、33元、450元、18元、169元、63元和277元。原料的总长度为600厘米,每单位原料的价值为0.5元。仿真结果如表2所示。
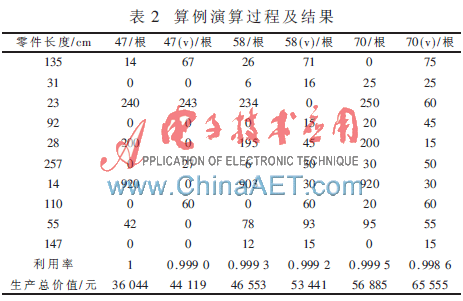
仿真实验结果显示,当原材料供应不足(此处仅针对原料短缺的情况进行探讨,而生产力短缺的情形与此情形相似)时,我们应着重于尽可能多地生产商品,以实现价值的最大化。其中,(v)指标表示考量因素。
在考虑价值因素对切割方式的影响时,通过仿真结果中的数据对比,我们发现:当原料无法满足生产需求时,若采用以价值为基准的切割方法,相较于忽视价值因素的切割方式,企业能够获得更高的利润。这一做法有助于在紧急情况下最大限度地创造价值。在此情况下,企业应优先生产价值较高的产品,并将其他产品的加工任务外包或采用其他形式处理。实验数据也证明了本文中提出的模型具有一定的实际使用意义。
本文聚焦于企业具体的一维下料难题,采用了蜂群遗传算法进行求解。通过实例分析,我们发现,在确保实现最高生产效益的同时,原材料的有效利用率同样达到了令人满意的程度,这对于应对实际生产中的突发事件具有重要的实践价值。


