刷脸背后，卷积神经网络的数学原理是这样的

刷脸背后，卷积神经网络的数学原理是这样的

《AI前沿资讯》致力于追踪人工智能学术探索、产业价值链、技术转化实践、边缘场景探索等方向的前沿电子传播平台。诚邀所有倾心于AI的业界同仁参与互动、分享见解、传播信息、贡献稿件，请务必点击“关注”，以便即时掌握全球人工智能领域的发展动态。计算机视觉技术已广泛融入日常生活，例如发朋友圈前自动美化照片，或网上购物时通过人脸完成支付，这些成功的应用都离不开卷积神经网络的巨大贡献。本文将介绍卷积神经网络背后的数学原理。

计算机视觉在自动驾驶、医疗和零售等领域能够实现一些过去看似无法完成的工作。如今，自动驾驶汽车和无人商店已不再是遥远的概念。实际上，我们日常频繁运用计算机视觉技术，例如用面部识别解锁手机，或在发布社交网络图片前自动美化。卷积神经网络或许正是促成这一系列成就的核心要素。这次，我们将借助卷积神经网络的理念，来加深对神经网络运作机制的认识。需要提前说明，全文涉及不少难度较高的数学公式，不过，读者也不必因为对线性代数和微积分感到头疼而气馁。我并非指望大家记住这些表达式，而是旨在帮助你们获得对基本原理的初步理解。

简介

先前我们接触过一种密集连接的神经网络，该网络中所有神经元被划分成多个组，组成了连续的层级结构，每个层级内部单元都与下一层级的所有神经元建立连接，下图展示了这种网络架构。

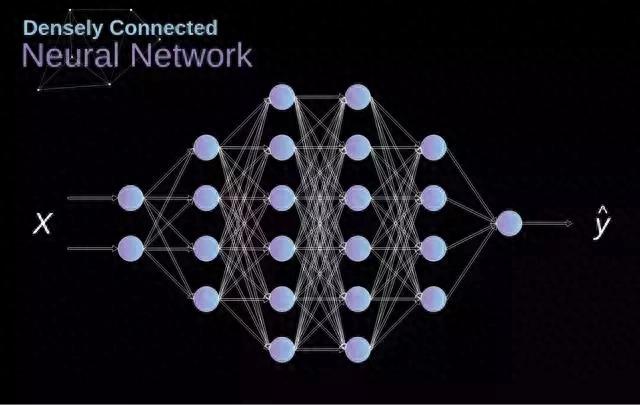
图 1 展示了网状交织的神经网络构造，这种办法在运用一个范围有限的固定数据集进行识别工作时十分有效——比如，我们通过分析运动员在竞赛期间积累的统计信息来判定他的岗位。然而，当面对图像数据时，情况变得更为错综。诚然，我们可以将每个图像点的明暗程度看作一个独立指标，随后将它送入密集型网络加以处理。很遗憾，要处理一张常见的手机照片开yun体育app入口登录，我们的网络需要包含成千上万的神经元，甚至达到亿级别的规模。此外，即便我们可以缩小照片的尺寸，也会导致一些重要的信息被丢失。因此，我们很快就会意识到，常规的做法已经不再适用——我们必须寻找一种新的高效方案，既要尽可能多地利用数据，又要有效降低所需的计算工作和参数数量。这就是 CNN 发挥作用的时候了。

数字照片的数据结构

我们先来简单说明一下数字图像的保存方法，图像本质上是一个庞大的数字阵列，阵列中的每个数值都对应一个像素点的明暗程度，彩色图像在 RGB 模型下由三个这样的阵列构成，分别对应红绿蓝三个颜色通道，而单色图像则只需要一个阵列。每个矩阵都记录着从零到二百五十五的数值，这个数值区间是图像存储信息效率与人眼敏感度之间权衡的结果，因为二百五十六个数值正好等于一个字节，同时人眼只能分辨出同种颜色中有限的几种色度

图 2. 数字图像的数据结构

卷积

核卷积并非仅限于卷积神经网络，它还是众多计算机视觉方法的核心部分，发挥着重要作用。具体操作如下：首先准备一个规模较小的数字矩阵，这个矩阵被称为卷积核或滤波器，接着将它作用于图像之上，依据滤波器的数值对图像进行相应的处理。最终特征图的数值，需要按照特定公式进行计算，该公式中，输入图像用 f 表示，卷积核则用 h 表示。计算结果的行列索引分别记为 m 和 n。

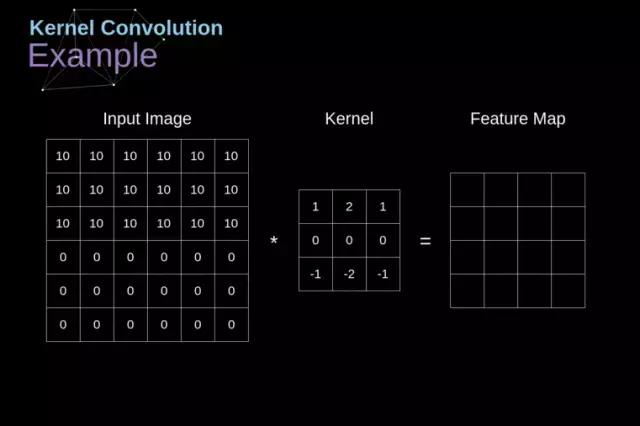
图 3 展示了核卷积的一个示范，当滤波器被置于特定像素后，卷积核中的每个数值都要与图像相应位置数值逐一相乘。完成所有乘法运算后，将各个乘积加总，所得和就填入输出特征图对应的坐标点上。通过动画可以细致观察这一运算细节，不过更值得关注的是整个图像经过处理后呈现的最终效果。图 4 展示了用数个滤波器做卷积的结果。

图 4. 用卷积核寻找边缘Valid 和 Same 的卷积

如图 3 所示，采用 3x3 的卷积核对 6x6 的图像进行卷积操作，会得到一个 4x4 的特征图。这是由于图像中只有 16 个不同的位置可以放置卷积核。又因为图像的尺寸在每次卷积之后都会减小，所以在图像完全消失之前，卷积操作只能执行有限的次数。另外，若留意卷积核在图像上的运行轨迹，便会察觉到，周边的像素点相较于核心区域的像素点，其作用力要微弱得多。如此一来，图像内蕴含的部分细节将会被牺牲掉，你能够从后图观察到，像素点的位移状态如何决定其对特征图产生的效果。

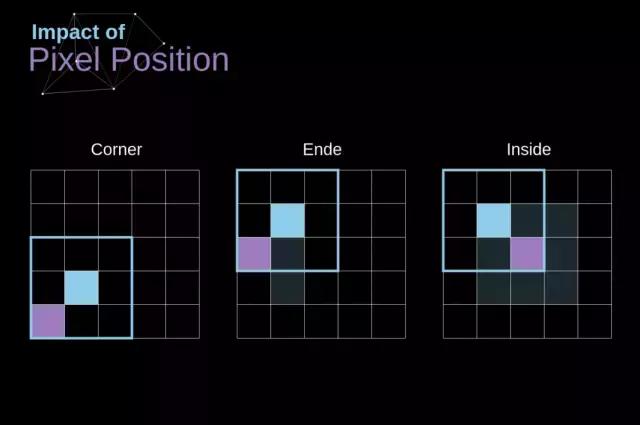
图 5 展示了像素位置的作用开元ky888棋牌官网版，针对这两个挑战，可以考虑增加一个额外的边界来扩充图像，比如采用 1 个像素的额外填充，那么图像的尺寸就会扩展为 8x8，进而使得 3x3 的滤波器运算后得到 6x6 的结果，在现实应用中，一般会选择用 0 来实现这种补充填充依据是否采用填充方式，将执行两种卷积运算——Valid式与Same式，这两种命名方式颇为费解，故作如下说明：Valid式指的是运算基于原始图像进行，Same式则是在图像边缘添加了边界，从而确保输入输出图像的尺寸保持一致。在第二种情形里，扩展的幅度需要符合下列公式，其中 p 代表填充值，f 指滤波器的尺寸，该尺寸一般取奇数

跨步卷积

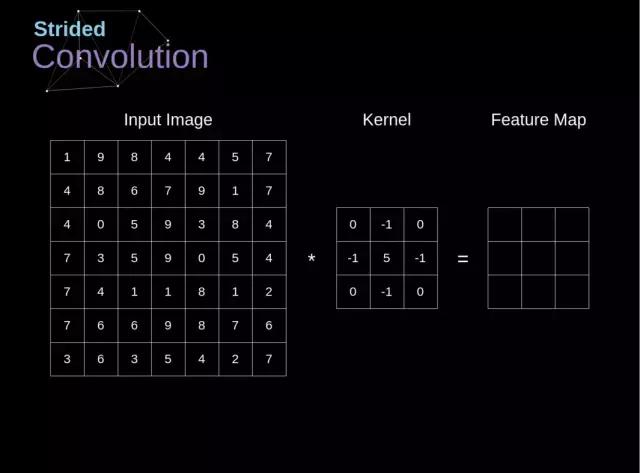
图 6 展示了跨步卷积的应用场景。在先前的案例里，卷积核的位置每次只挪动一个单位。实际上，步长也可以作为卷积层的一个可调变量。通过图 6 可以理解，当步长数值变大时，卷积操作会产生怎样的变化。构建卷积神经网络时，如果希望感受野减少重叠部分，或者让特征图的空间尺寸更小，可以考虑将步长调大一些。考虑到扩充和跨步，输出矩阵的维度可以使用下面的公式计算：

立体卷积转换到第三维度是一个关键性理念，它不仅使我们能应对彩色图画，并且尤为关键的是，能于同一层级部署多个滤波器。核心准则在于，滤波器与待施加滤波操作的图像必须具备相等的通道量。大体上，我们依旧参照图3的范例，不过这次从第三维度让矩阵中的数值彼此相乘。我们若需在同幅画面中使用好几个滤波器，会为每个滤波器分别进行卷积运算，接着把运算得出的结果逐个叠放，最终将它们合并成一个完整图像。所获取的三维矩阵，即张量，需满足以下公式，其中：图像的尺寸为 n，滤波器的尺寸为 f，图像的通道数量为 n_c，填充值为 p，步长为 s，滤波器的总数为 n_f。

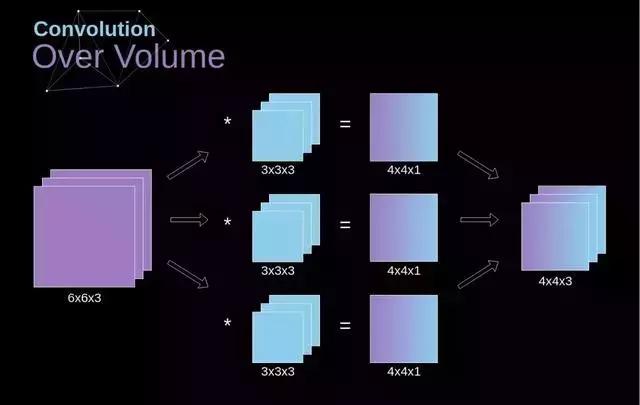
图 7. 立体卷积卷积层

现在需要运用今天学到的知识来构建一个卷积层了。我们的方法几乎和用于密集连接神经网络的方法一致，唯一的不同点在于不采用简单的矩阵相乘，这次我们将使用卷积操作。前向传播包括两个步骤。第一步是算出中间结果 Z，这个结果是通过前一层输入数据同包含滤波器的张量 W 进行卷积运算，再加上偏置项 b 后得出的。接下来需要针对我们的中间成果施加一个非线性变换，这个变换我们用 g 表示，喜欢数学公式的人可以在后面找到相应表达式，图示中展示了小型可视化，它描绘了方程中张量的空间结构

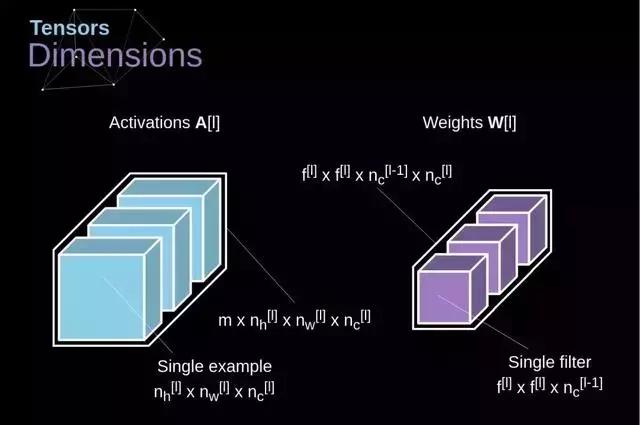
图 8. 张量维度连接剪切和参数共享

文章开篇，我已指出参数数量庞大是学习的难点，密集连接网络在图像处理上表现不佳。现在，关于卷积的知识已阐述清楚，接下来探讨其如何提升运算效率。这幅图中，2D 卷积的呈现方式略有不同，神经元通过数字 1 到 9 组成输入层来接收后续像素的亮度信息，A 到 D 这四个部分代表的是计算出的特征图元素，同样关键的是，I 到 IV 是卷积核中的数值，这些数值需要通过学习来获得。

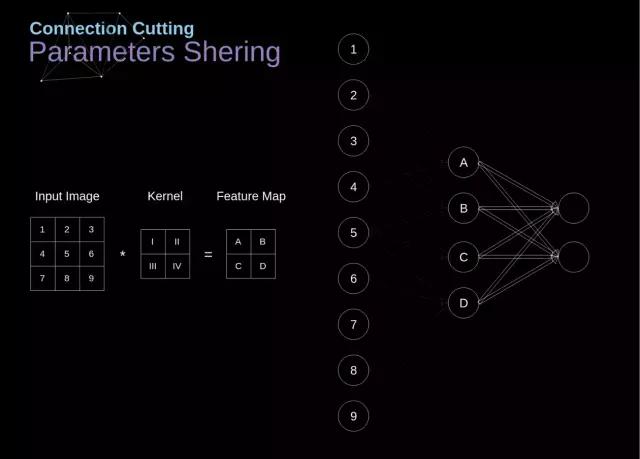
图 9 展示了卷积层的关键特征。首先，相邻的两个层级之间，并非全部神经元都建立联系。比如，神经元 1 仅对 A 产生作用。其次，部分神经元会使用相同的系数。这两个特点都表明，需要确定的系数总量会显著减少。要说明的是，滤波器的任一数值都关联到特征图的全部单元——这一点在逆向传递时尤为重要。

卷积层反向传播

尝试从头设计神经网络的人都明白，仅完成前向传递只是迈出了第一步，离成功还差得远。真正关键的部分在于后续的反向传递过程。虽然现在深度学习平台能自动处理反向传播，但我依然觉得弄清楚其内部机制很有必要。如同在众多节点交织的网状结构里，我们的任务是在一种称作逐步逼近的运算中求得变化率，接着凭借这些数值来调整系数设定。

计算时会借助链式法则，这个我之前在文章里讲过。我们希望考察参数变动对结果特征图的作用开元ky888棋牌官方版，再考察它对最终结果的效应。在深入细节之前，先统一下会用到数学符号——为了简化，我会舍弃偏导数的完整符号，改用下面这些简写符号。但是请记住，这个符号始终代表代价函数的偏导数。

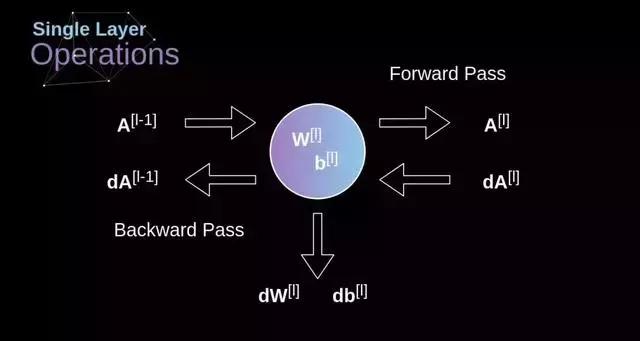
图 10 展示了卷积层在正向和反向传播时的输入输出数据，我们的目标是求出 dW 和 db，这两个量是针对当前层参数的导数，同时还需要求出 dA，它将传送到前一个层级。根据图 10，我们以 dA 作为计算起点，当然，这些对应的张量维度必须保持一致，dW 和 W 的维度相同，db 和 b 的维度相同，dA 和 A 的维度也相同。初始阶段需要利用我们的激活函数的倒数作用于输入张量，从而得出中间值dZ。依照链式法则，这个步骤的成果在后续环节将发挥作用。

当前，我们着手进行卷积神经网络的逆向传递过程，为此，将借助一种名为全卷积的矩阵运算——参见图示。需要留意的是，本环节所应用的卷积核会预先执行180度翻转操作。该运算可以用下列公式进行表述，其中滤波器以W表示，dZ代表一个标量，该标量源自前一级的偏导数信息。

图 11. 全卷积池化层

卷积神经网络除了卷积单元外，还会运用到一种称为池化单元的结构，这种结构最初设计的目的在于降低数据维度并提升计算效率，其构造相对基础，核心思想是将输入图像分割成若干网格，再对每个网格实施特定操作，以 Max Pool 为例，该层会从每个网格中筛选出数值最大的元素，并将其写入相应的输出位置和卷积层一样，我们也有两个可调节的超参数，分别是核的尺寸和移动的间隔。最后这一点也相当关键，在处理多通道图像时，每个通道的池化动作必须独立进行。

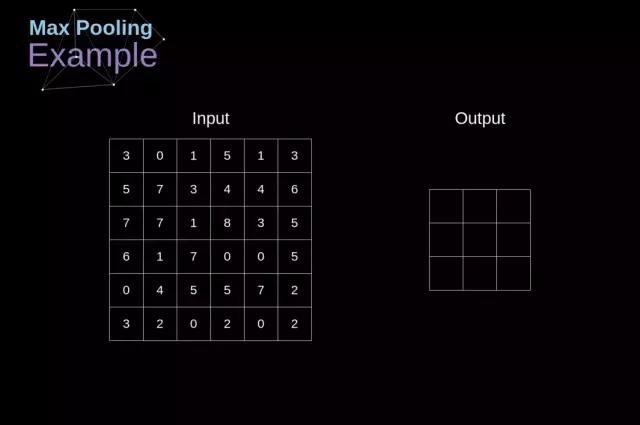
图 12 展示了最大池化层的一个应用案例，该层执行反向传播过程

本文仅探讨最大池化层的反向传播过程，但所获规则对各类池化层均适用，仅需略作修改即可。此类层内无需更新任何参数，因此关键在于恰当传递梯度。回顾前向传播阶段，我们选取各区域最大值，并将其传送至后续层级。因此反向传播过程也很明确，梯度不应对前向传播未涉及到的矩阵成分产生影响。具体而言，这是借助生成一个掩码来实现的，该掩码能够记录上一阶段数值的分布情况，以便后续传递梯度时加以利用。

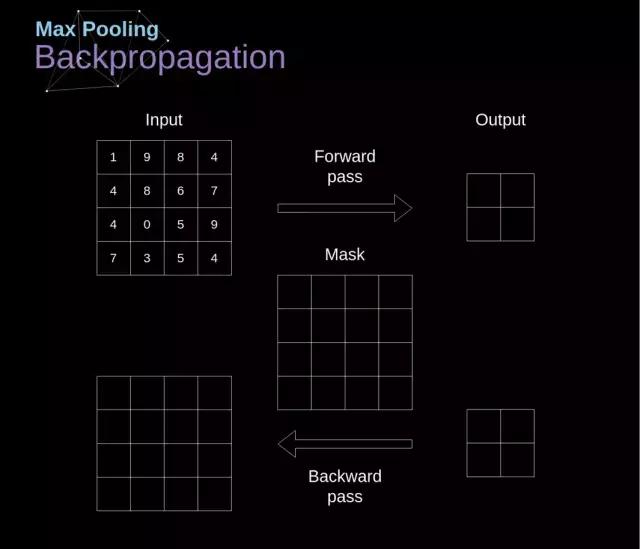
图 13. 最大池化反向传播原文链接：

朝向数据科学网站上的温和探索…

l ↩︎l ↩︎l -1 ↩︎l ↩︎l ↩︎