遗传算法解决最优化问题——基于python实现
最优化理论
最优化理论及算法属于核心数据领域,亦隶属运筹学范畴。该领域包含诸多分支,例如线性规划、非线性规划、整数规划、组合规划、图论、网络流、决策分析、排队论、可靠性数学理论、仓储库存论、物流论、博弈论、搜索论和模拟等。其核心任务是在众多备选方案中,识别出最优的那个方案。例如,在制造领域,怎样确定设计要素,才能让方案既符合标准又节省开支;在物资调配方面,怎样安排可用物资开元ky888棋牌官网版,才能既满足使用要求又获取最佳经济回报。
遗传算法
遗传算法属于众多寻求最优解的方法之一,它借鉴了达尔文生物进化论中的自然选择和遗传学原理,构建了一种计算模型来模拟生物进化过程,这种模型以群体中的所有个体为考察对象,借助随机技术,对一个经过编码的参数范围进行快速搜寻。遗传算法的遗传作用包含挑选、组合以及改变;参数的表示、初始种群的形成、适应度函数的制定、遗传作用的规划、控制参数的确定,这五个方面构成了遗传算法的关键部分。
从根本上说,遗传算法是一种筛选机制。它从最初的种群开始,依据适应度函数挑选出表现优异的个体,淘汰掉表现欠佳的个体开yunapp体育官网入口下载手机版,并持续进行。同时借助变异和交叉操作,逐步拓宽探索范围,最终确定出最理想的个体,这个个体即为问题的答案。
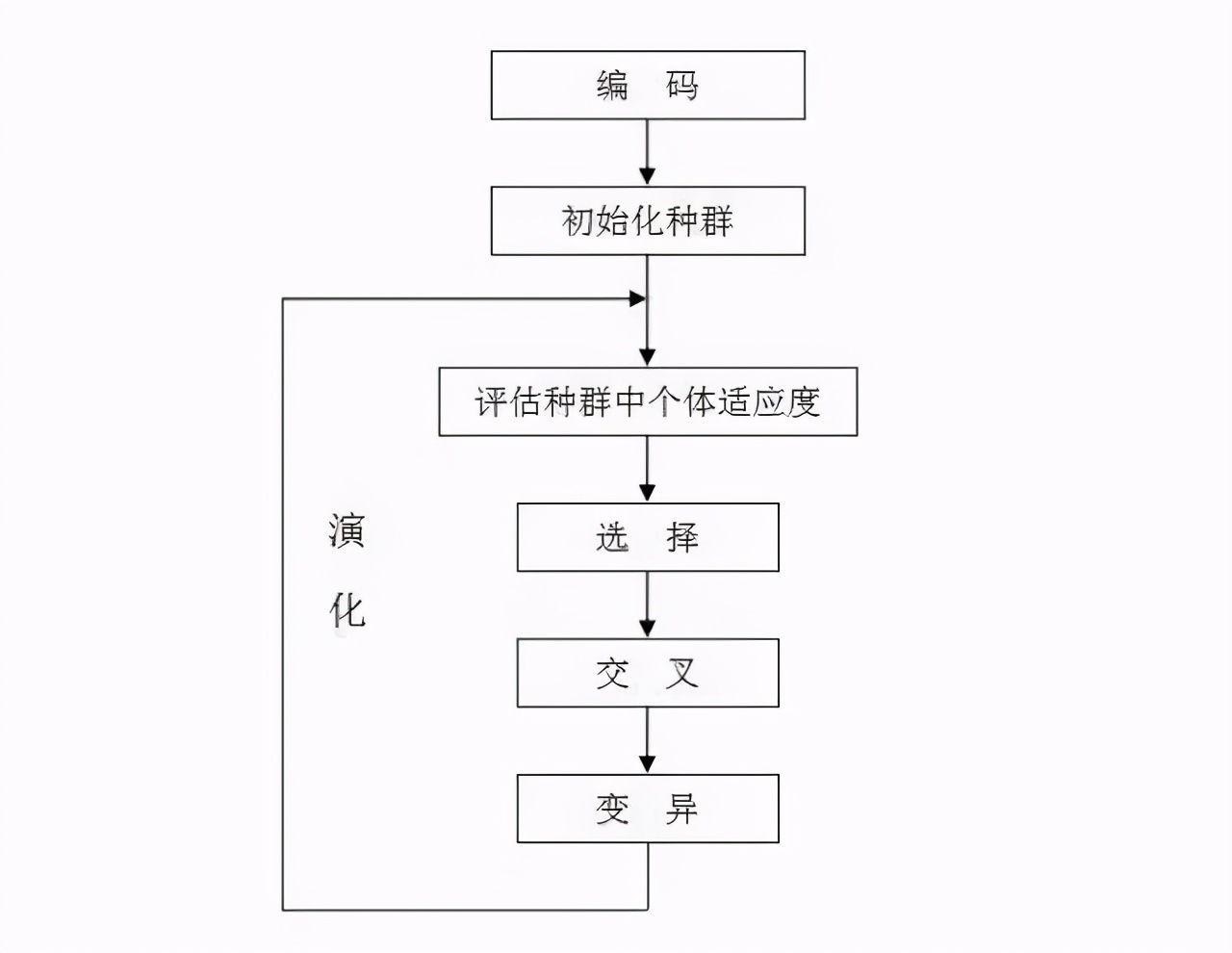
python遗传算法代码实现
以具体问题说明y等于2乘以正弦x加上余弦x的极值求解过程,剖析厨子解牛遗传算法的运作原理
初始化种群
建立含有population_size个个体的种群,每个个体拥有chromosome_length长度的二进制基因序列
#输入种群大小和染色体长度,染色体用列表表示
确定物种起源需要考虑种群规模和染色体长度,这两个因素密切相关,彼此影响,其中种群规模决定了遗传多样性的基础,而染色体长度则影响着基因信息的承载能力,两者共同作用,为研究物种的形成和演化提供了重要依据。
population=[]
#二维列表,包含染色体和基因
对于每一个个体,在规模范围内进行遍历
temporary=[]
#染色体暂存器
对于每一个基因片段的位置,依次进行操作,从零开始计数,直到达到基因序列的总长度。
临时列表加入随机生成的零或一,作为新元素
#随机产生一个染色体,由二进制数组成
population.append(temporary)
#将染色体添加到种群中
return population生成一个染色体长度为6,12个个体的种群
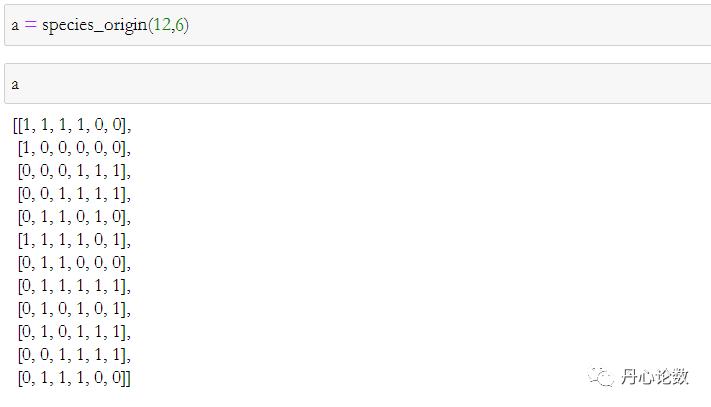
进制转换函数
#进制转换函数
计算种群规模,确定基因链长度,进行翻译处理
temporary=[]
对于群体中的每一个个体,依次进行遍历
total=0
for j in range(chromosome_length):
总数加上人口数组第i项第j项的值乘以二乘以j次方
#从第一个基因开始,每位对2求幂,再求和
二进制数0101换算为十进制数,等于1乘以二进制的第二位,加上0乘以二进制的第三位,再加上1乘以二进制的第四位,最后加上0乘以二进制的第五位,计算结果为1,加上0,加上4,加上0,最终得到5。
temporary.append(total)
#一个染色体编码完成,由一个二进制数编码为一个十进制数
return temporary种群a的转换结果

适应度计算
定义一个函数,接收三个参数,第一个是种群,第二个是染色体长度,第三个是最大值
temporary=[]
function1=[]
临时值等于翻译结果,该结果来自人口和染色体长度
# 暂存种群中的所有的染色体(十进制)
对临时列表的每个元素进行遍历,依次取出每一个值,然后执行相关操作,最后完成整个循环过程。
x等于temporary中的i项乘以最大值,再除以二进制位数减一的结果
一个基因对应一个决策因子,该算法首先将其转换为十进制,接着除以二的基因数量次方再减去一个常数。
function1里头加上个式子,算出来是2乘以正弦x再加上余弦x的结果
此处将二倍正弦函数与余弦函数之和定义为评价目标,同时作为个体适应度的计算依据
return function1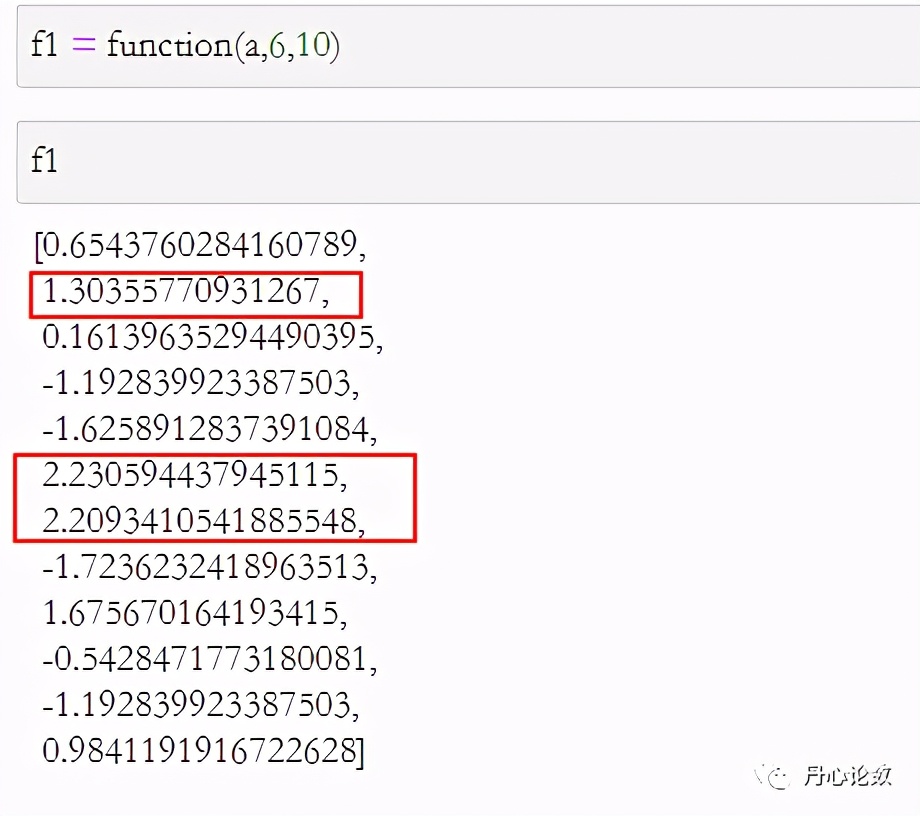
适应度函数用于选择优秀个体,适应度高的个体才会被选择
选择操作
#将小于0的适应度转化为0
def fitness(function1):
fitness1=[]
min_fitness=mf=0
对于function1的每一个索引位置,进行遍历,依次处理每一个元素,确保全部覆盖,完成操作
if(function1[i]+mf>0):
temporary=mf+function1[i]
else:
temporary=0.0
# 如果适应度小于0,则定为0
fitness1.append(temporary)
#将适应度添加到列表中
return fitness1
#计算适应度和
def sum(fitness1):
total=0
对每一项数据,依次进行操作,遍历整个数组,按照顺序,完成指定动作,在范围内,逐一检查
total+=fitness1[i]
return total
#计算适应度斐波纳挈列表,这里是为了求出累积的适应度
def cumsum(fitness1):
从倒数第二个位置开始向前遍历,依次访问每个位置,直到第一个位置
# range(start,stop,[step])
# 倒计数
total=0
j=0
while(j<=i):
total+=fitness1[j]
j+=1
#这里是为了将适应度划分成区间
fitness1[i]=total
fitness1[len(fitness1)-1]=1
#3.选择种群中个体适应度最大的个体
def selection(population,fitness1):
new_fitness=[]
#单个公式暂存器
total_fitness=sum(fitness1)
#将所有的适应度求和
for i in range(len(fitness1)):
new_fitness.append(fitness1[i]/total_fitness)
#将所有个体的适应度概率化,类似于softmax
cumsum(new_fitness)
#将所有个体的适应度划分成区间
ms=[]
#存活的种群
population_length=pop_len=len(population)
#求出种群长度
#根据随机数确定哪几个能存活
for i in range(pop_len):
ms.append(random.random())
# 产生种群个数的随机值
ms.sort()
# 存活的种群排序
fitin=0
newin=0
new_population=new_pop=population
#轮盘赌方式
while newin交叉操作
def crossover(population,pc):
概率阈值pc用于决定是进行单点交叉还是多点交叉,目的是创造新的交叉个体,但在此处并未应用
pop_len=len(population)
for i in range(pop_len-1):
随机选取一个数值,作为基因片段的起始位置,该数值介于零与该种群中个体基因长度之间
#在种群个数内随机生成单点交叉点
temporary1=[]
temporary2=[]
临时列表追加元素,取自数组指定项的前面部分,直到某个索引位置,包括该位置
临时列表追加子序列,从第二个个体的指定位置到当前个体的末尾,包括指定位置元素,不包括末尾元素。
将tmporary1用作临时存储,用来存放第i个染色体中从第0个到cpoint个基因,
接着,需要将第i+1条染色体从后cpoint到第i条染色体所含基因数量,追加至temporary2之后
临时列表添加了序列中从下标加一至截断点之前的所有元素,接着将这部分内容追加到目标集合中
临时列表接续子序列,从指定索引到末尾,包含所有元素,形成新组合
把临时变量二当作缓冲区,用来暂时保存第i加一编号个体中从零到c点位置的基因片段,
接着,将第i条染色体从后cpoint位置到基因总数之间的部分,添加到temporary2的末尾去
pop[i]=temporary1
pop[i+1]=temporary2
# 第i个染色体和第i+1个染色体基因重组/交叉完变异操作
#step4:突变
def mutation(population,pm):
# pm是概率阈值
px=len(population)
# 求出种群中所有种群/个体的个数
py=len(population[0])
# 染色体/个体中基因的个数
for i in range(px):
if(random.random()运行结果
需要把全部染色体的基因序列转换成十进制形式,基因最大值作为转换的上限,这样做是为了方便后续进行数据可视化展示
计算二进制数转换为十进制值的过程,需要设定最大数值范围,并确定基因序列的长度,通过这些参数进行转换,最终得到对应的十进制结果
total=0
for i in range(len(b)):
总和等于总和加上数组第i个元素乘以二的整数次幂
#从第一位开始,每一位对2求幂,然后求和,得到十进制数?
总数等于总数乘以最大值除以二乘以染色体长度减一的结果
return total
#寻找最好的适应度和个体
寻找最佳个体时,需要评估整个群体,依据其适应度值进行判断,从而筛选出表现最优的那个体,这个过程中要考虑多个因素,包括但不限于遗传多样性,以及个体之间的差异性,最终目的是找到那个适应度最高的个体,这个函数就是为了实现这个功能而设计的,它接收两个参数,一个是代表群体的数据结构,另一个是计算适应度的函数,通过这两个输入,函数能够计算出每个个体的适应度,然后进行比较,选出最佳的那个
px=len(population)
bestindividual=[]
bestfitness=fitness1[0]
for i in range(1,px):
# 循环找出最大的适应度,适应度最大的也就是最好的个体
if(fitness1[i]>bestfitness):
bestfitness=fitness1[i]
bestindividual=population[i]
返回最佳个体,返回最佳适应度值
population_size=500
max_value=10
# 基因中允许出现的最大值
chromosome_length=10
pc=0.6
pm=0.01
results=[[]]
fitness1=[]
fitmean=[]
种群=数量=物种起源(种群规模,染色体长度)
#生成一个初始的种群
对于群体规模中的每一个个体,都进行重复处理,具体重复五百遍
这个函数叫做function1, 它接受三个参数, 第一个是种群, 第二个是染色体长度, 第三个是最大值
fitness1=fitness(function1)
最优个体和最优适应度值由函数best对种群和适应度函数fitness1进行计算得出,结果分别赋值给best_individual和best_fitness变量
结果列表加入最佳适应度和通过最优个体计算得出的值,该值由特定函数基于最大值和染色体长度得出
#将最好的个体和最好的适应度保存,并将最好的个体转成十进制
挑选群体中的个体,依据其适应度值
crossover(population,pc)#交配
mutation(population,pm)#变异
results=results[1:]
results.sort()
X=[]
Y=[]
for i in range(500):#500轮的结果
X.append(i)
Y.append(results[i][0])
plt.plot(X,Y)
plt.show()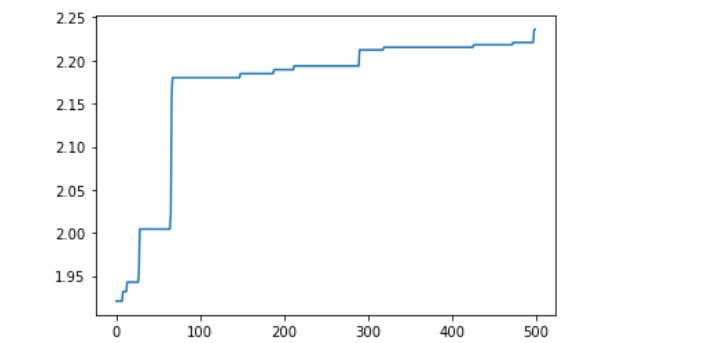
geatpy模块
geatpy是一个集成好的python遗传算法工具,下面通过实例来讲解。
求解
求函数f的最大值,当参数为x1, x2, x3时,其表达式为4倍x1加上2倍x2再加上x3
s.t.
2x1 + x2 ≤ 1
x1 + 2x3 ≤ 2
x1 + x2 + x3 = 1
x1 ∈ , x2 ∈ , x3 ∈ (0, 2)
import numpy as np
import geatpy as ea
创建名为MyProblem的类,该类继承自ea.Problem父类
def __init__(self):
name赋值为'MyProblem',这是对函数名称的一个设定,具体名称可以自由选择
M = 1 # 初始化M(目标维数)
目标列表初始为负一,代表默认极小化,正一代表极大利化,符号约定明确。
Dim = 3 # 初始化Dim(决策变量维数)
决策变量类型数组设置为初始值,每个元素都是零,数组长度等于维度大小,其中零代表可连续取值,一代表只能取离散值
lb = [0,0,0] # 决策变量下界
ub = [1,1,2] # 决策变量上界
lbin = [1,1,0] # 决策变量下边界
ubin = [1,1,0] # 决策变量上边界
# 调用父类构造方法完成实例化
ea问题类构造函数被调用时接受参数名称,决策变量数量,优化目标类型,维度大小,变量类型,下界值,上界值,固定下界值,固定上界值
这个函数是用于计算目标值的,接收一个种群作为参数,种群对象通过pop传入
Vars = pop.Phen # 得到决策变量矩阵
x1 = Vars[:, 0], 获取所有个体的x1值, 组成一个单独的列向量
x2 = Vars[[1], :] # 获取第二行所有数据形成列向量
x3 = Vars[2, :],这是从数据集中选取第三列,从而获得全部个体的x3值构成的序列
# 计算目标函数值, 赋值给pop种群对象的ObjV属性
pop.ObjV = 4*x1 + 2*x2 + x3
# 采用可行性法则处理约束, 生成种群个体违反约束程度矩阵
x1**2 + x2**2 - 1]) # 第三个限制条件
x1 + 2*x3 - 2, # 第二个约束
绝对值函数作用于x1, x2, x3三项之和与1的差值,作为第三个限制条件
引入 geatpy 库,命名为 ea
"""创建问题实体对象实例,完成对象构建过程,进行实例化操作,生成问题实例实体"""
问题对象已创建为实例,命名为MyProblem
"""==============================种群参数配置==========================="""
编码格式为RI,这种编码方法用于数据转换。
NIND = 50 # 种群规模
区域描述器被初始化,其参数包括编码方式,问题中变量的类型集合,变量的取值范围以及问题的边界条件,这些信息被整合在一起形成区域描述器实例
种群对象 eaPopulation 通过调用 Population 函数创建,该函数接收 Encoding, Field, NIND 三个参数完成实例化,但此时种群尚未完成初始化,只是生成了种群的基本框架结构
"""===========================程序配置信息=========================="""
算法模板对象被创建,命名为myAlgorithm,它通过ea.soea_DE_best_1_L_templet函数生成,该函数接收problem和population作为参数
该算法的最大迭代次数设定为一千次,这是其进化过程中的一个上限值。
我的算法的变异操作因子F被设为0.5,这是差分进化中的一个关键数值
我的算法的交叉概率参数调整为0.7
该算法的日志记录代数被设定为1,这意味着每隔一个世代就会进行一次记录,如果这个数值被设定为0,那么就代表不会进行任何日志记录活动
该算法的详细模式被开启,允许显示运行过程中的记录数据
该算法的绘图状态被设定为开启,具体表现为呈现图形输出,其中包括不进行任何图形显示的情况,或者展示最终成果的图像,亦或是生成目标场景中的动态演变过程,还有描绘决策领域中动态变化过程的影像
"""开始依据算法范例执行种群迭代过程,接着实施进化的相关步骤,然后依照范例框架推进种群演化,最后完成算法模板指导下的种群优化工作。"""
通过算法模板运行,获得了最佳个体,还有最终世代的全部种群
最优个体的数据已写入文档内,文件名定为BestIndi
"""=====================这里是最终呈现的文本内容===================="""
输出评估数量,其值为算法评估次数
计时已经到了,是 myAlgorithm.passTime 那么多秒了
if BestIndi.sizes != 0:
输出最佳个体目标函数的最优值,该值为BestIndi ObjV列表中第一个元素的第一个元素值
print('最优的控制变量值为:')
对于BestIndi.Phen的每一列,依次遍历
print(BestIndi.Phen[0, i])
else:
print('没找到可行解。')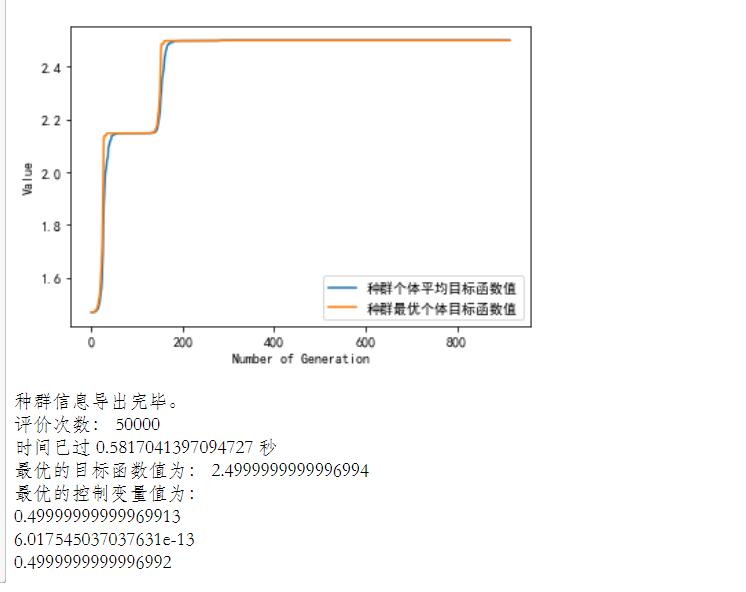
总结
最优化课题与常规机器学习领域有所不同,后者依赖海量数据来提取信息并建立知识体系,前者则面临不同挑战,关键在于如何将复杂决策转化为具备约束条件的规划任务,例如:车辆调配这一情形,能够表述为如下数学表达式:


通过python设定目标函数,确定适配度函数,适配度函数通常与目标函数一致,定义约束条件,并配置遗传算法的操作参数,包括染色体长度,编码方式,初始种群,选择比例开元ky888棋牌官方版,交叉点位置,变异比例



