3.2 遗传算法
3.2 遗传算法
遗传算法是借鉴自然选择原理的一种全局优化方法,它借助杂交、变异等操作来提升种群内解的优良度,从而帮助找到最佳结果。
3.2.1 遗传表达与编码
John Holland最初构想的遗传算法中,种群里的个体是以一段二进制序列来呈现的,这段序列被称作基因链,序列里的每一个二进制位则被称为基因,这两个名称都源自生物学领域
一个群体由若干基因片段构成,每个基因片段内含多个基因元素。基因片段通常象征群体中的一个完整生命体,换言之,它体现一个完备的方案或一种分类方式。有时基因片段也能相互融合,生成一个复合生命体,这种构造更贴近自然遗传过程,毕竟自然界中的生命体往往拥有成套的基因片段。借鉴Holland的理论,人们将基因片段视作一个完整生命体的象征。
基因在染色体上各自对应个体遗传特征的一个维度。有的基因作用单一,决定生物体特定部位的有无。多数情况下,基因之间相互关联,共同影响性状表现。比如在遗传算法中,染色体上的位置用来表示数学解题方案的二进制位值。
3.2.2 简单遗传算法
遗传算法的步骤如下。
(1)生成随机的染色体群(这是第一代)。
(2)如果满足终止标准,就停止;否则,继续执行步骤(3)。
(3)确定每条染色体的适应度。
(4)对本代染色体进行交叉和突变,产生下一代新的染色体群。
(5)返回步骤(2)。
研究对象的数量需要事先设定。多数情况下,这一数量在连续的世代间维持恒定。不过,调整群体大小在某些情形下具备实际意义。
各个染色体的体量通常是一致的,不过采用染色体尺寸可变的遗传算法也是可行的,只是一般情况下不会采用这种方法,需要在每一代挑选出适应力较强的染色体,让它们相互结合,从而繁衍出两个后代个体,由这些新生成的后代染色体集群来替代旧群体,同时也会让某些特别强健的父本能够繁衍出更多后代,并且让某些特定世代的成员得以留存至下一代。
1.适应度
遗传算法的常规形式需要一种标准来公正地评估染色体的优劣程度。比如,当用遗传算法对数字进行排列时,可以通过执行该算法并统计其正确安放数字的多少来判定其适应度值。此外,通过测量每个放错位置的数字和其本应所在位置之间的间隔,能够得到更为精细的适应度评估。
2.交叉操作
交叉操作应用于两条长度相同的染色体。
(1)选择一个随机交叉点。
(2)将每条染色体分成两部分,在交叉点处分裂。
通过把一条染色体的头部同另一条尾部拼接,能够修复断裂的染色体,也可以反过来操作开元ky888棋牌官方版,进而得到两条全新的染色体。
例如,考虑以下两条染色体。
可以在第六和第七基因之间选择交叉点。

现在染色体重组的部分如下。
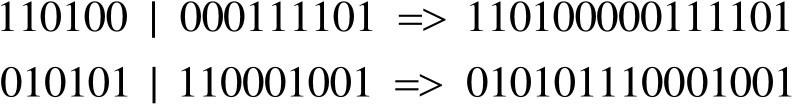
这一过程以人类繁衍时DNA链彼此交织融合为基础,也就是后代融合了双亲的基因特质。最普遍的做法是实施单一交换,不过也能选用存在两个或以上交换点的交换方式。
在两条线的交汇处,挑选两个节点,使染色体被划分为两个区域:外层区域和内层区域。外层区域被视为结合在一起,促使染色体形成环状结构。当交叉发生时,这两个区域会彼此交换位置,具体情况如图3-9所示。
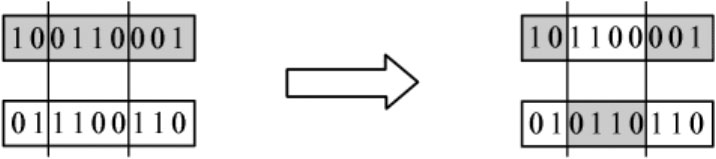
图3-9 两点交叉图解
在交织排列下,几率p用来判定后代采用父本1的某一位信息还是父本2的某一位信息,换言之,一个后代能够从它的双亲那里任意获取某个二进制位。比如,设有这样一对双亲个体。
父代1:10001101
父代2:00110110
能够确认这两条染色体的后代,如图3-10所示,来自父本1的基因以灰色阴影标示,来自父本2的基因则没有阴影。

图3-10 两个父代染色体进行均匀交叉产生两个后代
首个后代的初始位有p的几率源自第一亲本,有1-p的几率源自第二亲本;若首个后代选取自第一亲本的位,则第二个后代对应选取自第二亲本的位,反之亦然;不同于传统单点或双点杂交每对亲本产生两个后代,均匀杂交通常从一对亲本生成一个后代。
基因库里的基因确实能通过均匀交错大量融合,有时候选用极高(或极低)的p值非常恰当,能保证多数基因源自一个亲本(或另一个亲本)。某些时候可以运用无性繁殖的方式,完全不涉及配子结合,从而得到与亲本基因完全一致的新个体。
3.突变操作
遗传算法与常规的寻优技巧有诸多相似之处。寻优技巧首先构建一个潜在解开yun体育app入口登录,然后不断迭代寻找更优方案,直至无法获得改进。当面临局部最优解时,这种传统方法效果欠佳。为克服这一局限,遗传算法增设了变异操作。变异算子属于单一操作符,仅作用于一个变量,即单个基因,其执行频率一般不高,例如为0.01或0.001。基因突变仅会改变染色体内位点的数值。以0.01的突变率为例,在包含100个基因的染色体中,有可能有一个基因的值发生反转。接下来将展示针对前述情形的一个后代实施突变的具体情况。
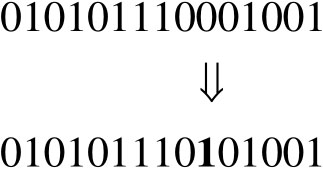
4.终止准则
遗传算法存在两种结束工作的情形:其一,事先设定进化次数的上限,超过该次数即停止运行;其二,针对某些问题,若获得特定解法或群体中最佳适应度值达到预设标准,则运行终止。在3.2.3章节会介绍如何运用遗传算法处理数学函数问题。在这种情形下,一旦找到准确解法,即可结束运行,因为这种情况下的测试非常便捷。
3.2.3 应用实例:数学函数优化
这里说明怎样借助遗传算法来确定数学函数的极值点,我们以某个特定函数为例进行探讨。
其中,x是用弧度计量的,x数值介于0到15之间。每条染色体用4位二进制数来记录x的数值。图3-11展示了该函数的分布形态。
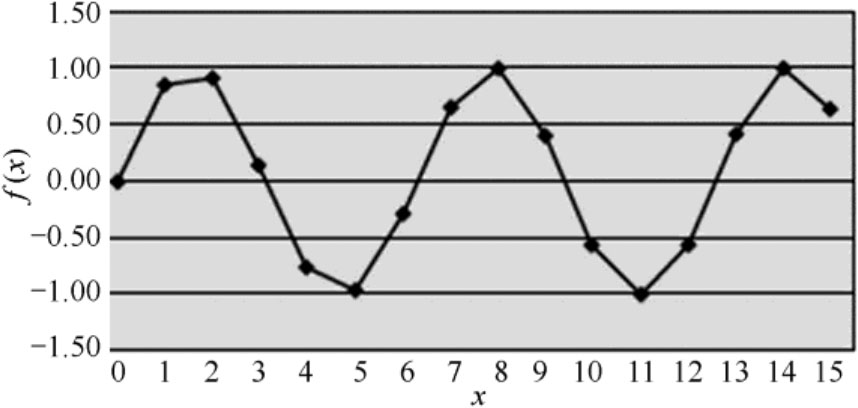
图3-11 展示了函数f(x)=sin(x)的数据点分布情况,其中x的数值范围介于0到15之间,每个数据点都对应于该函数在该x值处的计算结果
这个群体有四个染色体的个体,首先创建随机种群,作为初始世代。
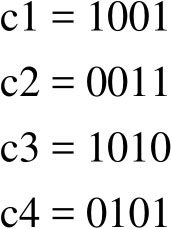
评估染色体的适宜程度,必须先把它变更为十进制数值,再求出该数值的f值。
把适宜程度设定在0到100之间,0代表完全不匹配,100代表完全匹配。
f(x)可以产生介于负一与正一之间的数值,当f(x)等于正一时,其对应值为最高适应度100,当f(x)等于负一时,其对应值为最低适应度0,而当f(x)等于零时,适应度设定为50,所以x的适应度情况
定义为
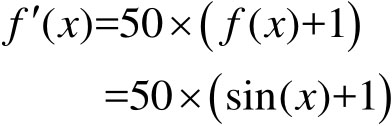
染色体在总适应度中所占的比重开元棋官方正版下载,就是它的适应度比例,接下来会解释这种算法为何十分实用。表3-2呈现了计算第一代适应度时的具体数据。现在要运用遗传算法来推算下一代,首要步骤是挑选需要复制的染色体,轮盘赌方法依据适应度比例随机挑选染色体进行复制,详细过程如下。
表3-2 第一代适应度的计算结果

将染色体适应度依据比例从零分配至一百,第一代中,c1适应度值介于零到四十六点三,占据整体百分之四十六点三,c2适应度值介于四十六点三到八十三点七,占据整体百分之三十七点四,后续染色体依此类推分配适应度区间。
现在产生一个介于零到一百之间的随机数值,这个数值会确定一个染色体的区间,接着选取该染色体进行繁衍,再生成另一个随机数值用于挑选该染色体的配对对象,这样一来,适应能力较强的染色体通常比适应能力较弱的染色体能够繁衍出更多的后代。
关键在于:这种做法不能阻挡基因较差的个体繁衍,因为这样做有助于保证种群不会因为同一个祖先不断繁衍而失去活力。
但是,在前面提到的情形里,染色体c4很难再次出现,这种情况只有在某个数值介于98.6到100之间时才会发生。
要挑选四个配对者繁衍后代,先抽取一个随机值,得到56.7,因此c2成为首个选定的亲本。接着又抽到一个数值38.2,由此确定c1为它的对应对象。
现在要借助c1和c2来生出两个新个体。必须随机确定一个配对位置,选在第二位基因与第三位基因的中间。
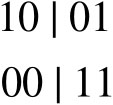
现在用交叉产生两个后代:c5和c6。
以同样的方法,c1和c3被挑选出来用来繁衍后代c7和c8,借助第三位和第四位之间的互换位置。
此刻,c1至c4构成的初始群体已让位于c5至c8形成的后续群体,c4因无法繁衍,其遗传信息将随之消逝
c1属于第一代最优的基因型,可以繁衍两次,这样就把其高适应性的基因传给了所有后代个体。
第二代的适应度值如表3-3所示。
表3-3 第二代的适应度值

这一代出现了两种匹配度高的染色体,也有两种匹配度低的染色体。实际上,其中一条c7染色体就是最佳方案。现在,终止条件可能判断程序是否能够终止;如果不能满足,程序会继续执行,却无法找到更优的方案。从初始状态转换到最优状态,可能只需要一次迭代就能实现。
这确实是个十分容易理解的案例,现实中的情况或许要复杂得多。这类问题或许会牵涉到数量更多的个体,其规模通常介于100到500之间,个体的基因串也可能容纳更多的二进制位。很多时候,遗传算法能够迅速为组合类挑战找到最佳或者非常接近理想的答案。



