【AI系统】卷积操作原理

卷积是神经网络中的关键运算方式，属于一种特殊的线性处理。卷积神经网络（CNN）是为图像处理任务设计的网络结构，它借鉴了猫的视觉感知原理，通过叠加卷积单元和池化单元来识别图像特征。CNN在计算机视觉领域取得了重大突破，推动了深度学习技术的快速发展。

卷积运算存在多种变体，其运算过程颇为繁复，神经网络在执行过程中很大一部分时间都用在了进行卷积运算上，神经网络模型的演进往往伴随着网络层数的增加，所以提升卷积运算的效率变得极为关键。

本文先说明卷积在数学上的含义，再借助信号处理方面的一个案例来讲解卷积的操作步骤。接下来，会阐述卷积神经网络中卷积运算的要点。掌握卷积运算的基本原理后，将介绍卷积在存储空间里的数据布局，并说明张量内卷积运算的具体实施方法。

卷积的数学原理

卷积通常作为一种数学运算，作用于两个实变函数。在泛函分析领域，卷积，又称旋积或褶积，是通过函数 f 和 g 生成新函数的一种运算。这种运算本质上属于一种积分变换，具体表现为函数 f 与 g 在翻转和平移后的重叠区域，其函数值相乘再对重叠区域长度进行积分的过程。

卷积神经网络这一概念源自信号处理中的卷积运算，信号处理领域的卷积定义如下：

能够说明，对于绝大多数实数 x ，当 x 发生变化时，积分会生成一个新函数 h(x) ，这个函数被称作函数 f 和 g 的卷积，用符号表示为：

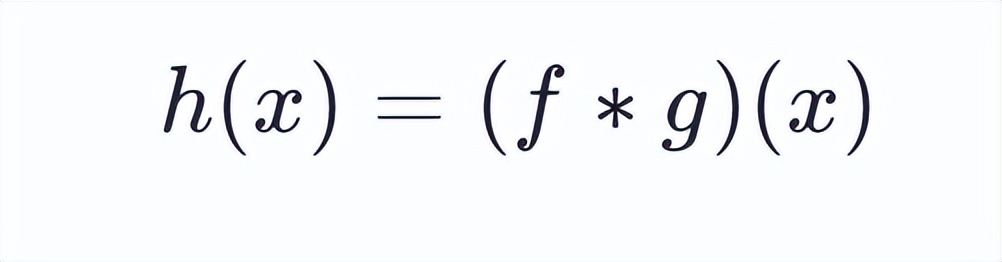
信号处理的卷积可以理解为一种连续表达方式，但在实际运算环节，这种连续性会被转化为离散形态来执行计算，

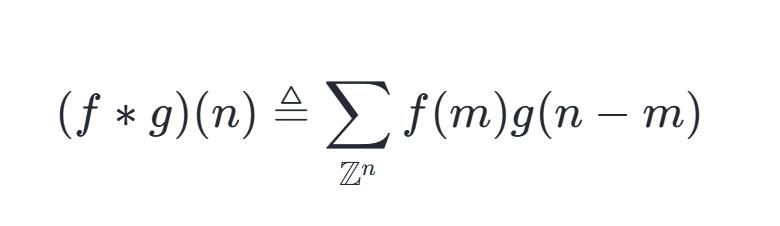
通俗定义

卷积运算的原理比较难明白，它的图像化表现如下所示。图中，红色的滑动条在移动时与蓝色的正方形相乘，所得到的三角形状图形，就是卷积运算在每个位置上的具体数值

更具体来说，解释卷积需要清楚“卷”和“积”两个步骤。

“卷”的过程

根据上述介绍中卷积的定义：

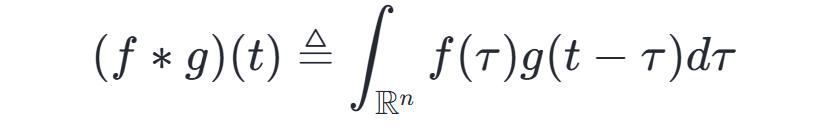
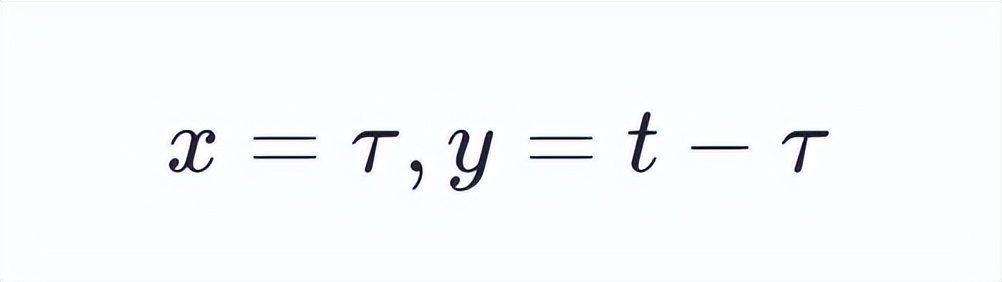
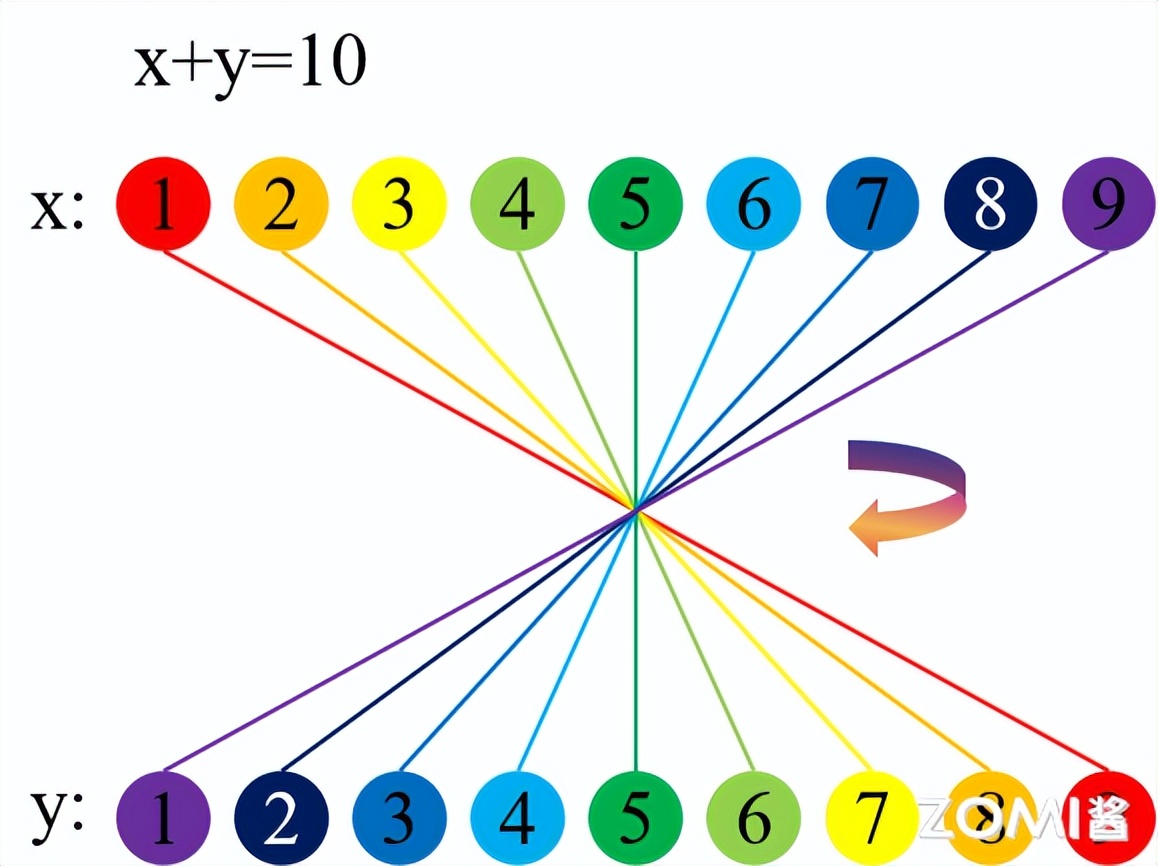
则有 x+y=t 成立。

换句话说，进行卷积运算时，函数 f(x) 和 g(y) 中 x 与 y 的数值变化遵循线性关系 x+y=t 的限制条件。当设定 t 等于 10 时，x 与 y 的数值分布呈现出特定的对应模式。从视觉上看，x 与 y 的数值排列具有某种镜像对称的特征。

2. “积”的过程

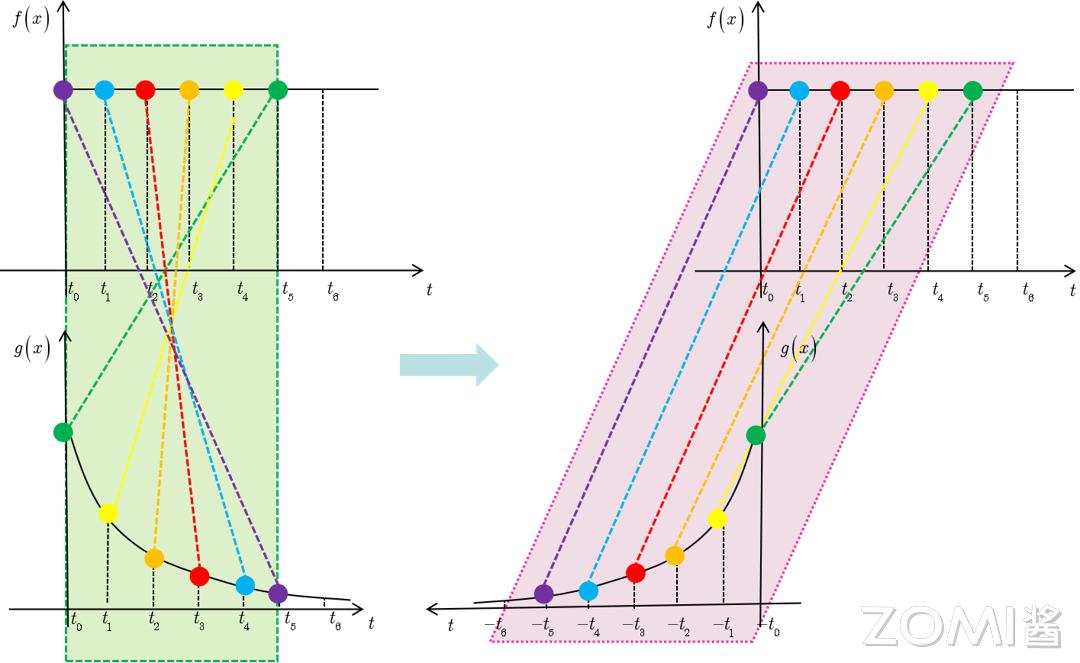
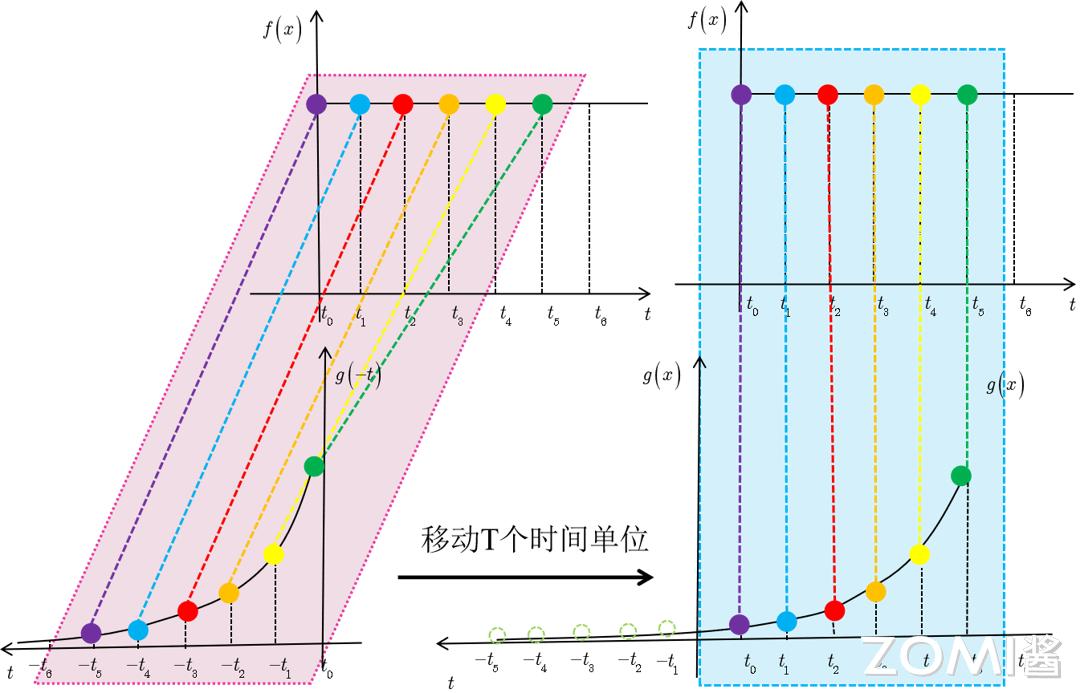
当 t 的数值发生改变，x,y 的数值范围始终被下图中的倾斜角度为负一度的直线系所限定。

定义：

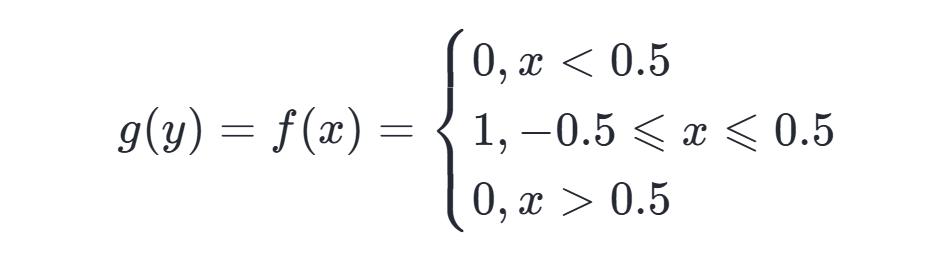
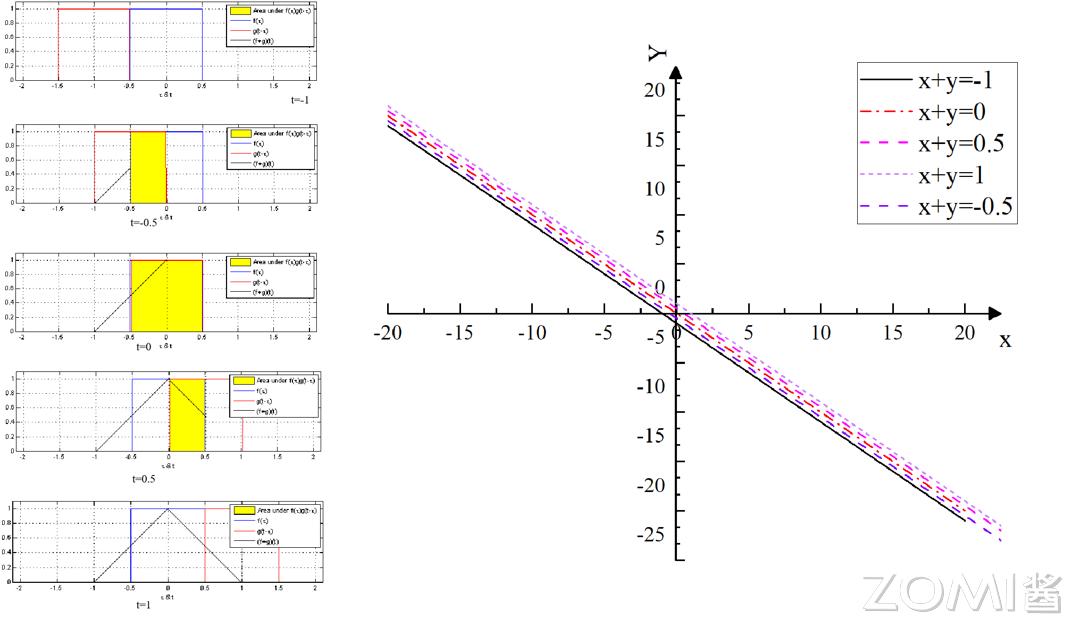
图左侧 t 的数值自上而下依次为负一，负零点五，零，正零点五，正一，设 y 等于 t 减去 τ，x 等于 τ，左侧图中的红色曲线代表 g 函数在 t 减 τ 下的形态，蓝色曲线代表 f 函数在 τ 下的形态，黄色部分标示出不同 t 数值时参与卷积运算的有效范围，黑色直线右端点的坐标即为卷积运算的最终值

总而言之，积分的内涵可以视为累加的终极形态，卷积中的“累积”环节就是两个函数进行乘法运算并计算定积分的步骤。

具体例子

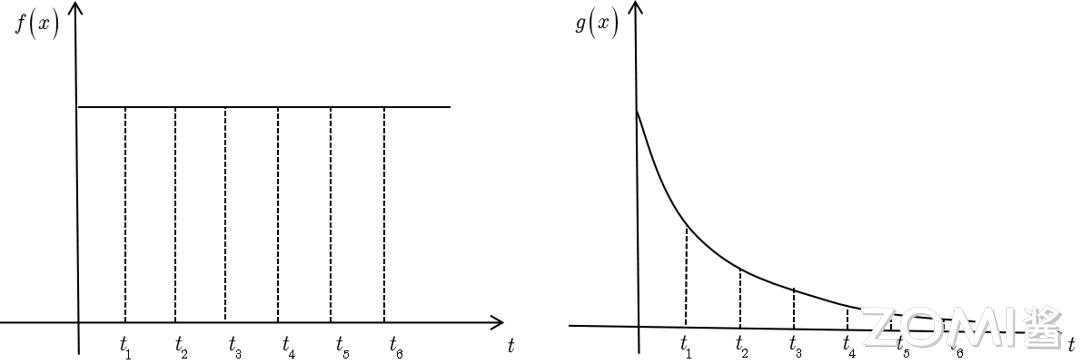
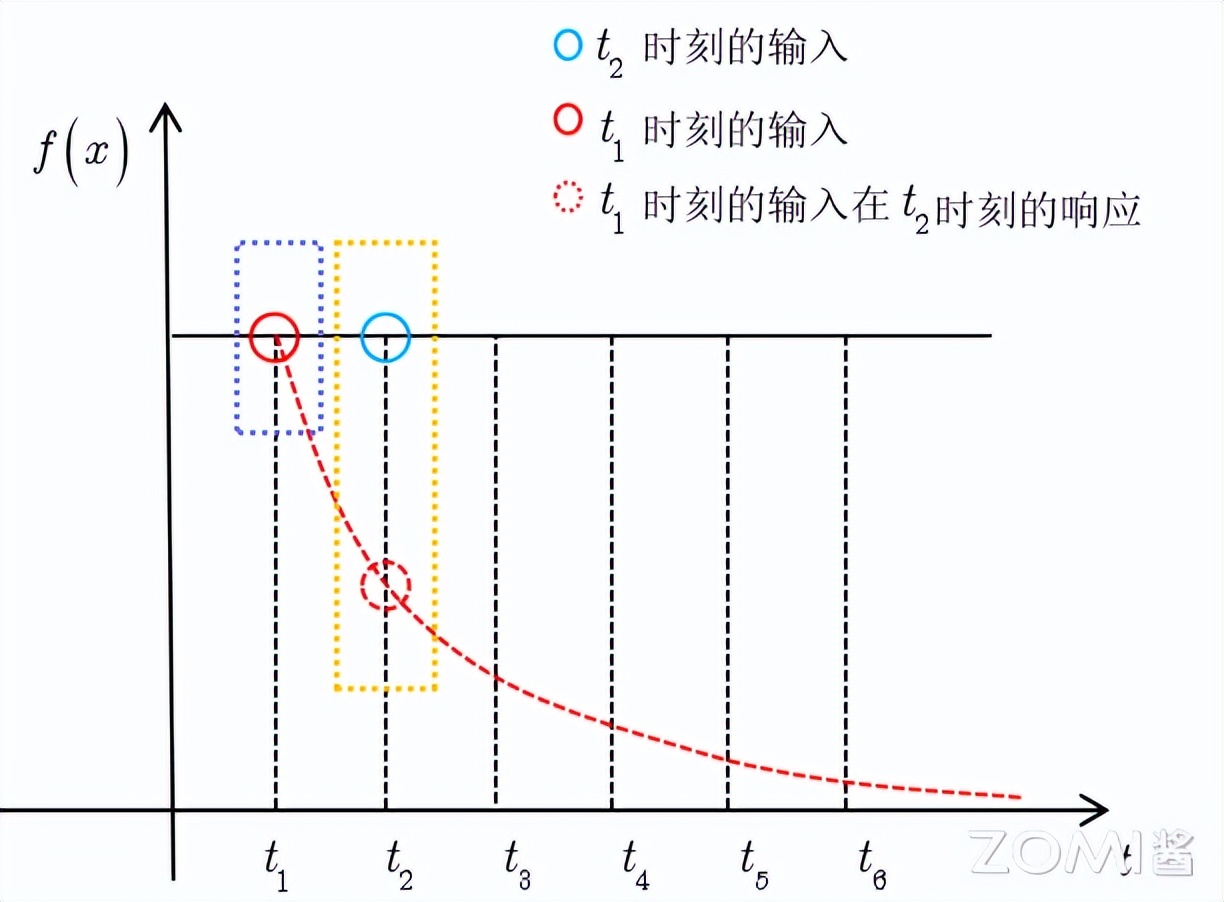
以信号处理的系统响应函数为例：

输入信号记作 f(t) ，其数值随时间推移而恒定不变。系统响应函数以 g(t) 表示，如图所示该函数呈指数形式递减，其物理内涵在于：倘若在 t=t1 的时刻施加一个输入，那么随着时间的持续，该输入将会逐渐减弱。

卷积的性质

卷积满足以下的数学定律和具体的性质：

运算满足交换特性，即 f 与 g 的运算结果等于 g 与 f 的运算结果；运算具备结合特性，即三个元素 f g h 的运算顺序不影响最终结果；运算存在分配特性，即 f 对 g 与 h 的和进行运算等于 f 分别对 g 和 h 运算后的和；运算包含单位特性，即存在一个特殊函数 δ ，任何函数 f 与 δ 运算都等于 f 本身。

其中 δ 代表狄拉克 δ 函数，在连续情况下使用，在离散情况下则称为单位脉冲函数。

卷积物理意义

卷积的实际含义要看它被用在哪个专业范围，在不同的专业范围里，卷积能够体现不同的物理现象。

信号处理

信号处理中，卷积的作用常与系统特性相联系。设有一个输入信号 f(t) ，比如音频波形，同时存在一个系统对此信号的反应 g(t) ，即系统的输出。该系统反应 g(t) 可能是理论上的完美模型，也可能是实际采集到的数据。

输入信号 f(t) 送入系统后，系统的输出 h(t) 可以借助卷积 f∗g 来求得。这种卷积运算能够体现系统对输入信号的累积效果。具体而言，h(t) 在任意时刻 t 的数值，是输入信号 f(t) 与系统特性 g(t) 在所有先前时刻的乘积之和。权值取决于系统回应g，这体现了系统对各个时间点输入信息的“留存”。

若某个体系对于外来信息的反馈存在延迟现象，那么其产生的结果函数 h(t) 便会成为原始激励函数 f(t) 的一个均化形态，具体的平滑效果则由函数 g(t) 所规定。

2. 图像处理

图像处理领域，卷积运算常用于实现滤波操作和完成特征提取任务，图像可看作是二维信号f(x,y)，其中f(x,y)代表图像的横向位置，y表示图像的纵向坐标，卷积核g(x,y)则是一个小型的权重矩阵，该矩阵在图像上进行移动，用以计算每个像素点所对应的加权数值平均值

这项工作的实际作用在于逐一对照图像中的每个像素与其邻近的像素，借助带权数的平均计算来得出该像素点的新数值，卷积核 g 的构造方式决定了这种对照的具体方法，比如用于边缘识别的卷积核能够强化图像内亮度剧烈转变的部位，进而找出轮廓线

3. 概率论

概率论领域表明，两个互不影响的随机变量的联合概率密度函数经过卷积运算，能够导出它们相加后的概率密度函数。从物理角度来看，设有两个随机事件，各自对应随时间演变的概率密度函数，当这两个事件叠加形成新事件时，其概率密度函数可通过将原两个概率密度函数进行卷积运算来求解。

4. 其他物理系统

在别的物质现象里，混合能够说明弥散情形、震动行进、物料掺和等。在这种情形下，混合说明了某个物理指标，比如热度、力度、丰度等，在时日和方位上的分布转变，这是由系统里各处之间的互相影响和传送作用慢慢积聚造成的。

概括而言，卷积的实质在于借助特定手法，将两个函数（或信号）融合，从而得到一个新函数，该函数从某个角度体现了这两个函数的相互影响或融合程度，具体内涵则因应用范畴和函数（信号）的物理属性而异。

离散卷积

从上文信号分析的部分中，我们得到离散形式的卷积公式：

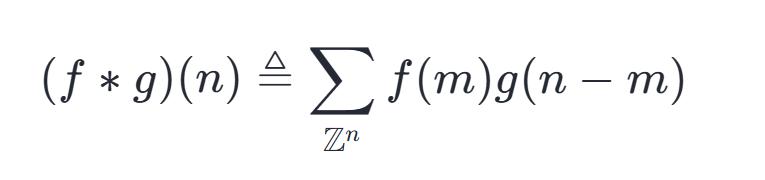
离散卷积是一种运算，它针对两个离散序列，将对应位置的元素相乘，然后将所有乘积加起来，得到最终结果。

离散卷积能够理解成矩阵的相乘，不过，其中部分元素要满足必须和另一些元素相等的约束条件。举例来说，在单变量离散卷积的情境下，矩阵的每一行元素，都与上一行对应位置向右平移一个单位的元素完全一致。这种矩阵被称作 Toeplitz 矩阵。

将那个分散的卷积算式扩展到平面坐标系，就能得到神经网络里的卷积操作，可以概括为：

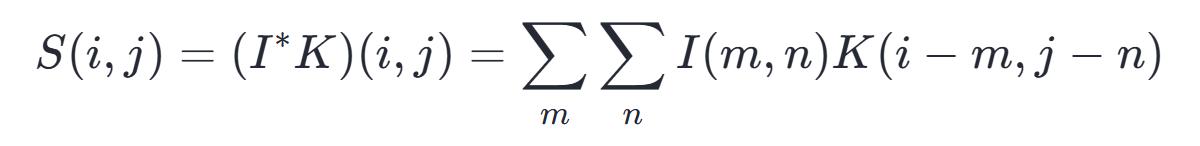
其中：S代表卷积运算的结果，I表示卷积的原始数据，K指卷积核的边长大小。由于卷积运算满足交换律，我们也可以等价地表述为：

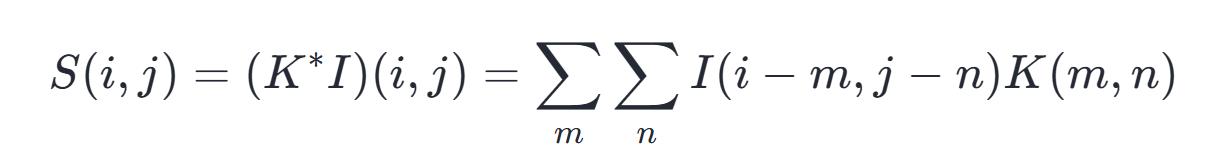
在二维情形下，卷积表现为一种双重嵌套循环的矩阵形式，这种矩阵的元素在特定位置满足约束条件，整体结构却极为稀疏，其稀疏性源于卷积核的尺寸远小于处理图像的像素总量，任何不依赖矩阵固有构造特性的、基于矩阵乘法的神经网络算法，均可直接应用于卷积运算开yun体育app入口登录，且无需对神经网络模型进行重大调整

卷积运算中，首个变量 f 代表输入数据，第二个变量 g 表示核函数。运算结果称作特征映射。在机器学习领域，输入多为多维度数组形式，核则通过学习算法调整，成为多维参数数组。我们称这些多维数组为张量，因为输入与核中的每个元素都需要单独存放，我们一般假定除了存储数值的特定点集外，这些函数的值都是零，这表明在具体运算时，能够通过计算有限个数组元素的加和来完成无限求和的过程

CNN 卷积计算

卷积神经网络由三个基本单元组成。首先是卷积单元，这是整个网络的关键，它通过在图像上执行卷积运算来识别图像中的关键点。卷积单元的输入一般包含多个维度，比如一张多通道的图片，每个维度都对应一个特定的特征。经过处理后，卷积单元的输出同样包含多个维度，每个维度都代表着一种不同的特征信息。池化层可以减小特征图在空间上的尺寸，同时还能加强模型面对图像位移时的稳定性和抗干扰能力。全连接层一般用来处理卷积层和池化层得到的信息，进行分类或预测。这个层接收的是线性排列的数据，其输出数据的多少取决于具体任务需要分辨的类别数量或者预测值的复杂程度。

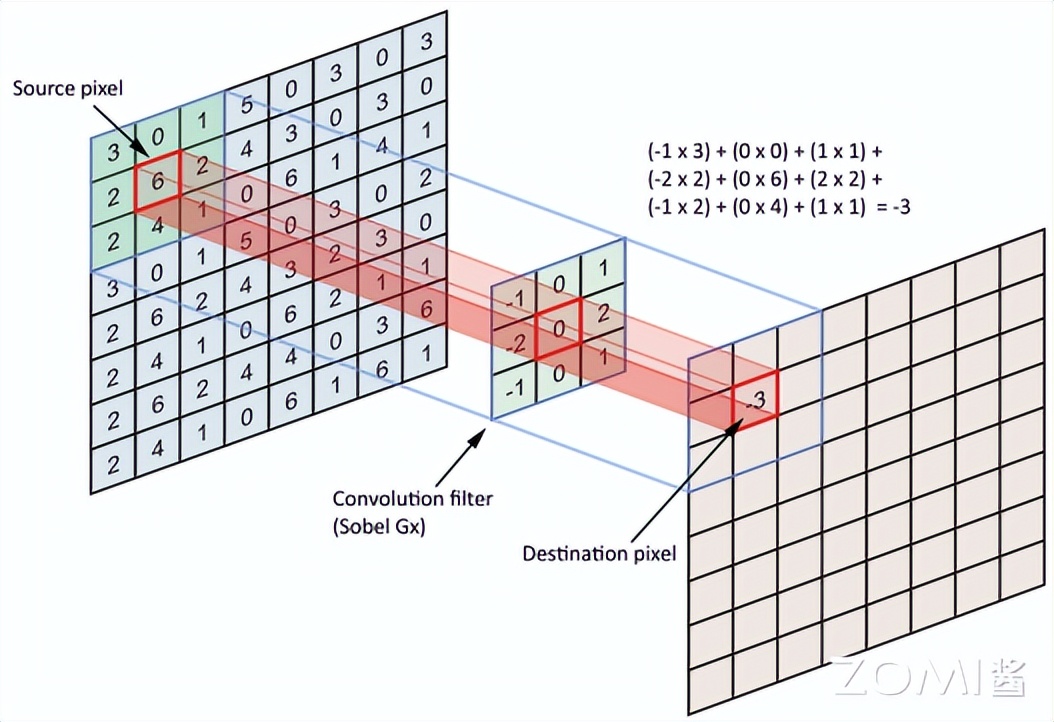
如图所见, 神经网络里的卷积运算可以这样说明：一个 3∗3 的滤波器在 8∗8 的像素矩阵上移动, 每次移动都要将滤波器与当前覆盖的像素值相乘并累加。那个蓝色部分就是它的作用范围。

名词解释

卷积运算包含诸多特定术语和多样计算方法，例如填充、步长、通道、内核等，接下来将详细阐释这些术语的内在联系和具体含义。

扩充（Augmentation）：为了保护图像角落细节不被忽略，会在原始影像的外围增加若干行和列，一般选用“0”作为补充材料。这样做是为了确保经过卷积处理后，输出图像的像素数量保持原样，便于推算特征分布的尺寸，同时修正边缘区域的信息缺失问题。

运作的内在机理是，设有 n×n 的图形，以 k×k 的滤波器执行卷积运算，其结果矩阵的维度为 (n−k+1)×(n−k+1) 。由此引出两个弊端：

处理这两个情况时，我们采取的措施是进行填充，假设填充的行列数量为 p，由于在四周都增加了一个像素单位，因此结果就变成了一个 (n+2p−k+1)×(n+2p−k+1) 的矩阵。

填充方法一般包含三种类型：全零填充法、等宽填充法和指定填充法。

Valid 方式

长方形的尺寸会缩小，具体来说，原始图像的边长为 n，而卷积核的边长为 k，计算之后，结果矩阵的边长会变成 n 减去 k 再加一，也就是 n−k+1，这个新的尺寸会出现在输出的图像中，形成一个小正方形，其边长同样是 n−k+1，整个过程中，没有进行填充操作，直接通过卷积运算得到最终结果

Same 方式

相同的意思是补充之后输出的尺寸和输入的尺寸相同。基于初始输入计算出的输出尺寸为 n−k+1 ,在补充 p 行/列之后,公式变为 n+2p−k+1。让 n+2p−k+1 等于 n,这样输出和输入的尺寸就会一致,解出 p 的值为 (k−1)/2。这就形成了两种情形。当 k 为奇数时，能够直接通过公式求得 p 的值；当 k 为偶数时，必须采用非对称的填充方法，例如左侧填充更多，右侧填充更少，以此来维持输出尺寸不变。

自定义方式

设定特定行列数量即为自定义操作。设图像宽度为 w，高度为 h，那么由此生成的特征图尺寸可以用下列公式确定：

步长指的是卷积核在每次卷积过程中移动的间隔。这个间隔的数值会决定最终结果的规模，同时也会关系到图像特征的捕捉程度以及运算的繁简程度。如果步长数值变大，那么输出结果的体积就会变小，图像细节的提取效果会下降，不过运算效率会相应提高。

将 Stride 的操作理解为对全卷积运算结果进行降维处理，当需要在输出结果的各个维度上每隔 s 个单位选取一个点时，或者当卷积核在图像上移动步伐为 s 时，这个行为可以用数学公式来表述

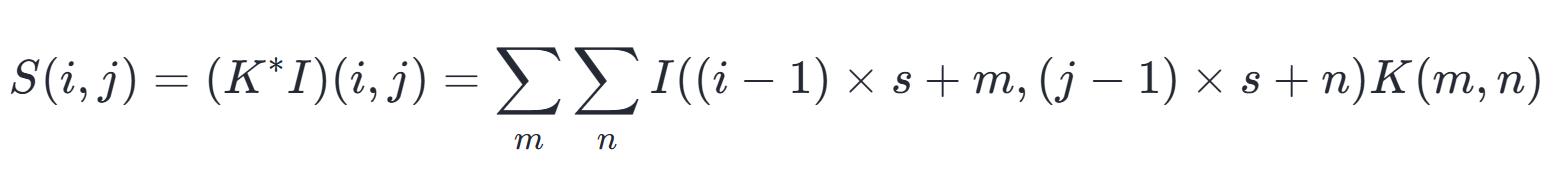
通道数量，也称作深度或特征图的总数，表明卷积神经网络每一层所输出特征图的个数。这个数量直接关系到网络提取特征的能力，也决定了计算任务的多寡。提升通道数量能够强化网络识别特征的效果，不过同时也会让计算变得更加繁重。

卷积核是一种带有可训练参数的工具，其作用是从输入图像中提取特征，最终产生特征图。每个卷积核对应一种特定的模式或特征，卷积核的数量决定了特征图的张数，一张特征图由一个卷积核生成。在机器学习领域，卷积核的参数值是通过反向传播和梯度下降方法自动调整的，并非人为预先设定。它的主要特征包括：卷积核每次仅覆盖 K×K 的像素范围，K×K 代表着卷积核的规格；卷积核的参数在整个处理过程中是循环应用的，并且会在图像上进行移动扫描。

朴素卷积过程

为了更清晰掌握后面要谈的例子开元棋官方正版下载，先把卷积神经网络 CNN 各层的相关指标说明一下，包括它们的具体数值，以及这些参数如何设定，都列出来，让大家看明白。

H：图片高度 hight；

W：图片宽度 width；

C：原始图片通道数 channel；

N：卷积核个数 Number of Kernel；

K：卷积核高宽大小 Kernel Size；

P：图像边扩充大小 Padding；

S：卷积核窗口滑动的步长 Stride。

设定 P 等于零，S 等于一，以六个卷积核对一张宽度为五，高度为五，通道为一的图像实施卷积运算时，所经历的步骤如下：

一个卷积核所影响的 3×3 的区域，其中各点数值相乘再求和。每个卷积核都对这样一个区域执行乘积求和运算，并且把来自不同通道的值加在一起（在这个例子中每个卷积核的通道数量是 1），最终计算出特征图相应点的数值。

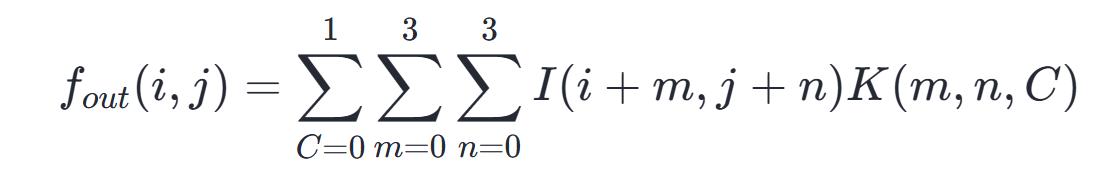
1,2 步骤的过程如下图所示。

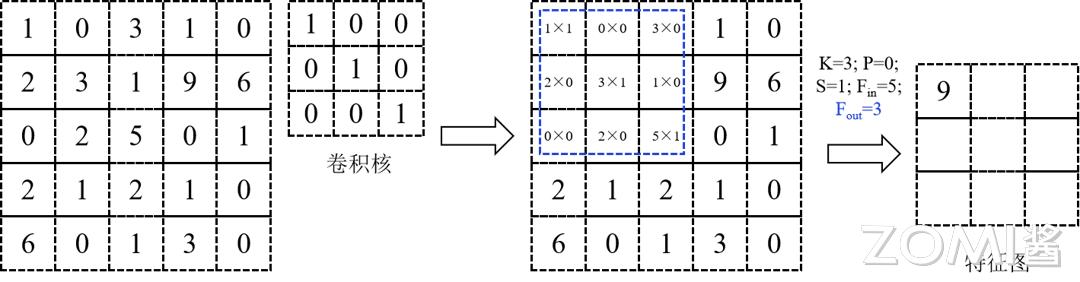
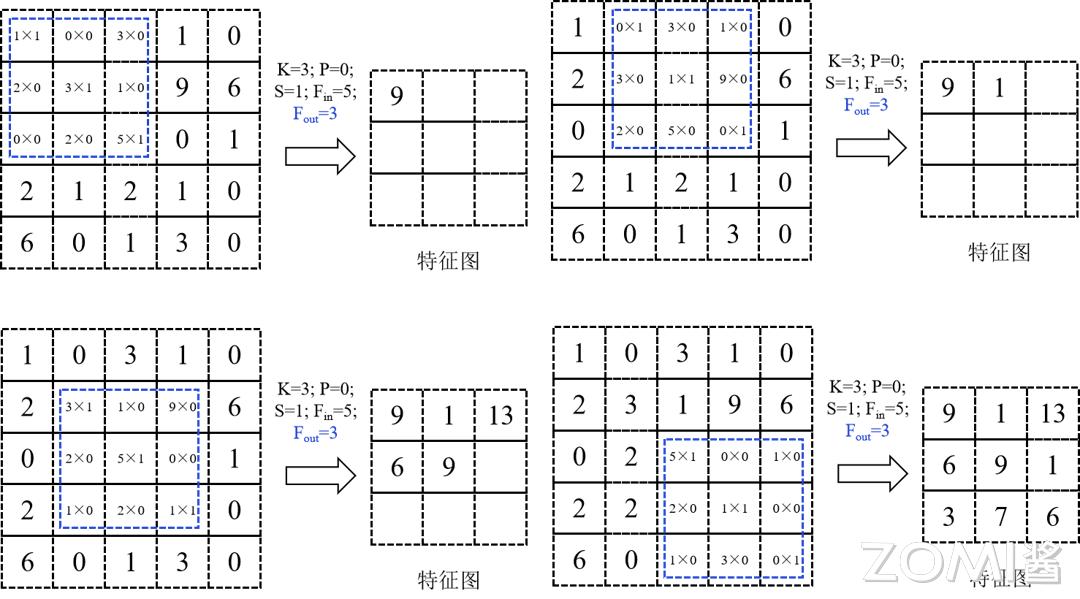
每一次滑动，都会在第 l 个特征图上得到一个像素点，如图所示。所有滑动次数的总和，就等于特征图包含的像素点数。

如果存在多个路径，比如设定条数为三，那么每个路径上位置对应的数值需要逐一合并，最后得出总数值。

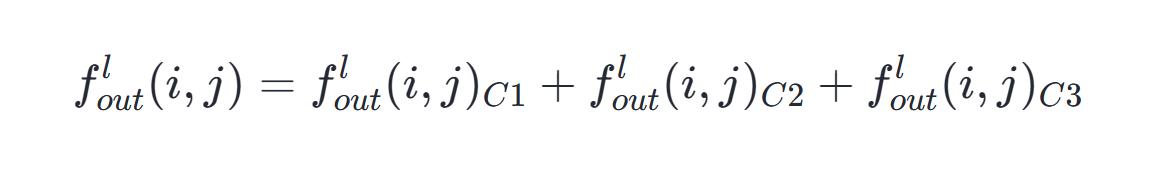
进行卷积神经网络的层级间运算时，完成前两个环节后，通常会加入偏置项 b，此举旨在消除网络的空间对称性，进而提升其学习性能。

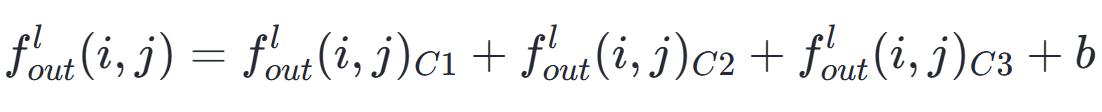
卷积运算里，卷积核属于可训练的参数，其参数的调整依据梯度下降算法。通过前面的说明，可以了解到每一层卷积的参数总数为 C 乘以 K 乘以 K 乘以 N。卷积层包含的参数不多，这个特点源于卷积层仅连接局部区域以及共享权重的特性。

单个神经元仅与输入神经元的一个特定部分建立关联，这个特定部分被称为感受野。在图像卷积运算时，神经元在空间位置上是局部关联的，具体表现为在图像平面上滑动区域进行操作，然而在深度维度上，即通道层面的计算，神经元之间则实现了全面连接。这种局部关联确保了训练完成的卷积核能对局部的输入特征产生最敏锐的反响。

权重共享意味着同一个输出特征图使用相同的卷积核，这个卷积核在输入图像上移动，生成一张特征图。每张特征图的每一个点，都是通过这个卷积核在输入图像上移动并进行卷积运算得来的。这种方式能够显著降低参数数量。卷积层一般使用多个卷积核来识别不同特征，每个卷积核内部的不同通道各自拥有独立的权重值，例如 RGB 图像就有三个通道，每个通道的权重值是单独设置的。同时，同一个卷积核的所有通道会共享一个偏置参数。

计算复杂度分析时间复杂度

CNN的运行效率关键在于卷积部分的处理负荷。单个卷积层所需时间，能够用公式来描述

整个 CNN 的时间复杂度由所有卷积层的时间复杂度加总得出。因此，要降低 CNN 的时间复杂度开元ky888棋牌官网版，可以采取减少卷积层数量的措施，或者降低每个卷积层的计算负担。例如，可以通过选用尺寸更小的卷积核，减少卷积层的通道数量，或者采用运算效率更高的卷积算法来提升 CNN 的性能表现。

在本文的后续内容会为大家介绍卷积的优化算法。

2. 空间复杂度

存储需求，从严谨角度分析，由整体参数规模和各层级生成图像特征共同构成。

因此，内存消耗的大小跟整体堆叠的层级数量，以及每一层里头进出的数据管道数量，还有卷积核的体积都有关系。

提升卷积神经网络的内存占用通常借助削减模型内部元素的多少达成。譬如，能够运用核函数拆解的技术，把一个体积较大的卷积核拆分成好几个体积较小的卷积核，以此裁减模型内部元素的总量。再者，亦可借助剪枝、数值化等手段，持续压缩模型的繁杂程度。

pytorch 卷积实现

首先定义 padding 模式。

计算填充值，需要输入数据，滤波器尺寸，以及模式类型
    """
返回不同模式下的填充列表
    params: inputs (input array)
参数：核大小，取值范围为p和q
返回：填充序列为 n, m, j, k
    """
    pad = None
    if mode == "FULL":
pad = [ks的首个元素减一, ks的第二个元素减一, ks的首个元素减一, ks的第二个元素减一]
    elif mode == "VALID":
        pad = [0, 0, 0, 0]
    elif mode == "SAME":
pad等于空格括号内第一项减去一除以二,第二项减去一除以二,
第一个数等于第一个元素减一之后除以二,第二个数等于第二个元素减一之后除以二]
        if ks[0] % 2 == 0:
            pad[2] += 1
        if ks[1] % 2 == 0:
            pad[3] += 1
    else:
        print("Invalid mode")
    return pad

选定输入的规格、卷积的窗口大小、填充的数值以及步长，输出的规格也就随之明确了。接着，根据这些指标来推算特征图的体量，然后设定卷积的操作。

进行转换，需要传入数据，卷积核，步长，以及模式参数，默认为等长模式
    # 确定卷积核的尺寸
    ks = kernel.shape[:2]
获取填充的样式和尺寸
这个pad值是通过调用get_padding函数获取的，输入参数包括inputs和ks，并且指定模式为SAME
填充后的输入数据等于对原始输入进行扩展，扩展的维度为三个，其中第一个维度在前后分别增加 pad[0] 和 pad[2] 个元素，第二个维度在前后分别增加 pad[1] 和 pad[3] 个元素，第三个维度保持不变，扩展方式采用常数值填充
    # 得到输入图像的尺寸和通道数
高度, 宽度, 通道数 = 输入数据的维度
    # 确定输出特征图的尺寸
out_width等于将width加上填充两侧的值再减去核大小的一半，然后除以步长，最后加一，结果取整
out_height等于将高度加上第一个填充值和第三个填充值减去第一个核大小值除以步长再加一的结果转换成整数
输出数组用零初始化, 形状为行数和列数, 具体为高和宽, 值都设为空
    # 进行卷积计算
将填充输入的形状减去滑动窗口后半部分长度再加一的结果，除以步长，得到起始索引，按顺序逐个取出，同时记录当前索引
对于填充输入的每一列，从零开始逐段遍历，步长为指定的间隔，每次移动固定的距离，同时记录当前的位置和索引，直到达到允许的最大范围为止
outputs的r行c列等于padded_inputs中从y到y加ks1,从x到x加ks0的区域与kernel逐元素相乘后的和
    return outputs

卷积优化手段Tensor 运算

张量涵盖了标量、矢量、矩阵等概念，并且是其延伸，在机器学习领域是基础的数据结构，程序里的张量表现为一种多维数组形式的数据结构。

#define MAX_DIM 6
struct Tensor {
    // 维度信息
    size_t dim[MAX_DIM];
    uint8_t num_dim;
    // 数据信息
    float* data;
    size_t num_data;
};

零阶张量仅由一个数值构成，一阶张量与向量概念一致，二阶张量相当于矩阵形式，三阶张量则表现为立方体结构。

张量

张量与张量之间的转换称作张量运算。在编程领域，其表现为接收多个张量作为参数，同时生成多个张量作为结果，并且过程不会对外部环境产生任何改动，这与函数式编程中的特性相吻合。

张量由两个核心部分构成，分别是维度和数据，张量运算也涉及这两个核心部分的处理。例如矩阵乘法 C = MatMul(A, B)，首先需要依据输入的张量 A, B 来确定 C 的维度，然后根据 A 和 B 的具体数值来计算 C 的数值。详细过程可参考后续代码展示。

张量*矩阵乘法函数张量A张量B{
    Tensor* C = new Tensor;
    // 计算维度
    C->num_dim = 2;
    C->dim[0] = A->dim[0];
    C->dim[1] = B->dim[1];
    // 分配内存
C结构体中的data指针指向动态分配的内存空间，该空间大小等于C结构体中dim数组前两个元素的乘积与浮点数大小规格化的乘积，通过malloc函数完成分配过程。
    // 计算数据
    Matrix::multi(C, A, B);
    return C;
}

Tensor 内存布局

NHWC 与 NCHW 是卷积神经网络中常见的数据排列方式，它们规定了多维数据，例如图像、点云或特征图，在内存中的保存顺序。

NHWC这种数据排列方式，将通道信息放在最后一个维度，这种布局是TensorFlow系统以及众多计算推理平台所采用的标准设置，作为它们处理数据的基准格式

NCHW（样本量，通道维度，图像高度，图像长度）表示数据排列顺序，其中通道维度位于高度和长度维度之前，这种格式在 PyTorch 框架中较为常见。

Tensor 卷积运算

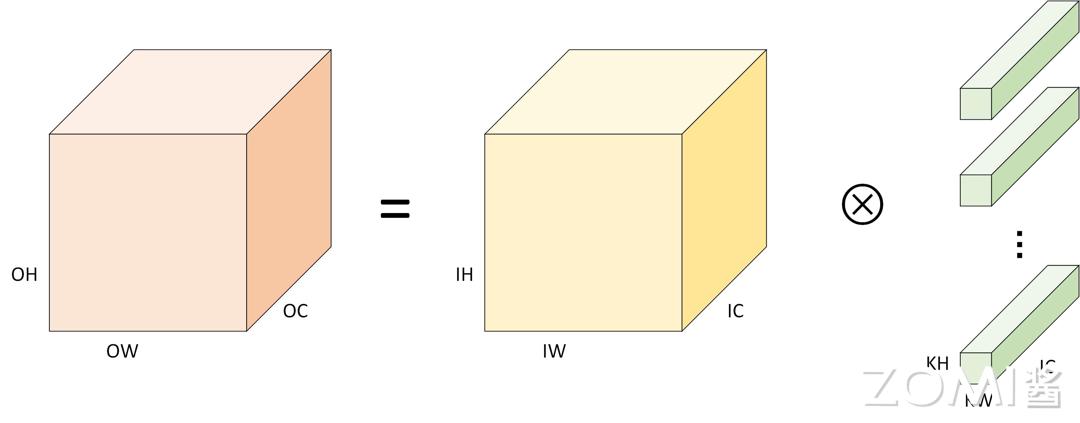
当张量存储方式为 NHWC 格式时，卷积运算的模拟代码如下，外三个循环负责遍历输出通道 C 的全部数据点，每个输出点都需通过内三个循环完成逐项相加（即点积运算）

for (int oh = 0; oh < OH; oh++) {
  for (int ow = 0; ow < OW; ow++) {
    for (int oc = 0; oc < OC; oc++) {
    //OH,OW,OC 为输出图像的尺寸和通道数，ow,oh,oc 为输入图像当前像素点的坐标和通道序号
      C[oh][ow][oc] = 0;
      for (int kh = 0; kh < KH, kh++){
        for (int kw = 0; kw < KW, kw++){
          for (int ic = 0; ic < IC, ic++){
          //KW,KH,IC 分别为第 i 个卷积核的尺寸和通道数，卷积核的通道数 IC 应与输入图像的通道数相匹配
            C[oh][ow][oc] += A[oh+kh][ow+kw][ic] * B[kh][kw][ic];
            //表示在输入图像的 ic 通道下 ow,oh 位置开始进行卷积计算，ow+kh 表示在 ow 处右移 kh 个位置
            //+=操作表示不同通道下的乘加结果求和，应“简单卷积过程”文章下步骤 3 的第二个公式
          }
        }
      }
    }
  }
}

针对矩阵运算的改进思路，我们同样能够运用向量化处理、并行执行、循环展开等基础技巧来优化这项计算。

若需深入AI领域资讯，可与该领域专家互动，请即刻前往昇腾社区网址https://www.hiascend.com/，或仔细研读《AI系统：原理与架构》此书，其中收录了丰富的AI学习资料和操作教程，能为您的AI技能提升注入强大助力。此外，您能够参与全国性昇腾人工智能大赛和昇腾人工智能开发者交流盛会等大型活动，从而探索人工智能领域的诸多未知之处~