pg下载官方认证 浅析统计学在实际生活中的应用

赵娅汐

说来也是近些年来，跟着招投标制度于我国持续发展，各种各样的评标计策已然有着颇为广泛的运用，而最低价中标法身为当下国际里最为盛行的评标办法，理所当然也就被运用到各个行业范畴当中，物资采购工作恰恰就是其中的一项，鉴于此，本文针对低价中标法予以了简要的介绍，并且针对其在物资采购里实际的运用给出了一些相对可行的提议。

【关键词】最低价中标;物资采购;招标人;竞标人

统计学，是一门应用性极强的学科，它是其他自然科学可利用的重要工具，还被应用于社会经济生活诸多方面。在学校教学与学习期间，因该学科涉及较多抽象概念和理论，若仅照教材宣科讲解理论，不结合具体实例，很难取得较好教学效果，同时，学生也很难真正理解与掌握统计学相关理论知识。鉴于此，对统计学在实际生活中的具体应用展开专门研究，具有重要现实意义。

一、统计学在生活中所发挥的重要作用

统计学，因其自身所具备的应用特性，故而并非如众多人所认为的那般，与人们日常生活关系不紧密。恰恰相反，它与我们的日常生活关联紧密，于我们身边，处处皆可见到与统计学知识相关的实例。比如，在我们搭乘高铁、飞机前往外地出差或者旅行时，尽管存在发生意外的可能性，然而因概率极低，所以我们常常就将其忽视，进而继续乘坐；媒体为获取大众针对某个热点事件或者话题的整体看法pg下载，而在街头随机对路人展开采访等等 。非但如此呀，统计学依靠它特有的属性，于我们的生活里发挥着越发重要的作用呢。就社会范畴以及经济管理层面来讲哦，借助统计学理论能够让政府、企事业单位做出更契合实际情况的决策哟。比如，政府为了获取有关人口、收入、国民生产总值、教育普及水平、就业率等方面情况，借助对调查所得数据开展统计与分析，能够对社会整体的相关指标情形做出估计，进而给制定相关政策措施递上可靠的数据支撑，企业为了达成自身发展对拟施行的项目予以评估与选择，会考察各个项目的期望利润，接着和企业的发展目标作比较，进而挑选出与企业发展目标相近、契合企业风险承受能力的项目等 。对于个人认知与决策而言，运用统计学理论能够强化个人对事物的理解跟认识，这对做出更优决策是有益处的。比如说，大家都清楚pg下载网站麻将胡了，买彩票中奖的几率是非常低的，然而却有一些人在这上面耗费大量时间以及金钱，期望获取巨额回报 。如果这些怀有特定学识之人，能对彩票购买持有更为清晰之认知，进而做出更为理性之决策，而非盲目追逐超额回报，且是以获得统计学知识为前提保障；当个人针对股票证券施行投资行为时，若能掌握统计学知识，即在详实剖析过往数据基础之上，合理预估目标公司之期望业绩，如此便可做出契合市场规律之投资决策 。

二、统计学在生活中的各种具体应用

（一）统计学在彩票问题中的应用

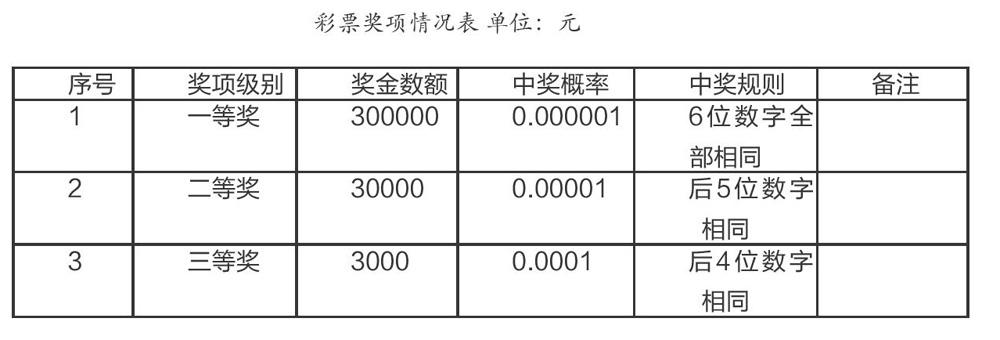
彩票于我们生活里是极为常见的，国家因要筹集各方面建设资金，常常会向社会发行一定数量彩票，不管是对发行方来讲，还是对身为购买方的个人来说，都能够借助统计学相关知识对结果作出合理估计，比如，假定某彩票发行中心发行一组总数为100万张且兑奖数字为6位数的彩票，每张彩票售价是3元，奖项设有三个类别，具体情形见下表：

通过上面的表格可知，奖项存在三类之分，这三类奖项分别是一等奖、二等奖以及三等奖，它们各自有着不同的中奖规则，具体规则是，彩票数字与兑奖数字只要全部相同，便会获得一等奖，彩票数字与兑奖数字后五位全部相同，就会得到二等奖至于彩票数字与兑奖数字后四位全部相同，那便荣获三等奖。获得一等奖需要彩票所有数字都准确无误，如此一来它的中奖概率等于06，也就是0.000001，相应的是，二等奖的中奖概率是0.00001，三等奖的中奖概率为0.0001 。据之可得，就个人来讲，每购一张彩票所获期望回报，等于3000乘以0.0001，加上30000乘以0.00001，再加上300000乘以0.000001，其结果等于0.9元，然而购买一张彩票所付花费是3元，所以除去极少特殊情况，个人购买彩票都是支出多于收入，不会有超额回报产生，。对于彩票发行方来讲，彩票发行带来的总收入是300万元，要付给彩民的奖金是0.9乘以100万等于90万元，形成的盈余为210万元，能把这部分盈余投放至社会其他方面进行建设。

（二）统计学在证券投资决策方面的应用

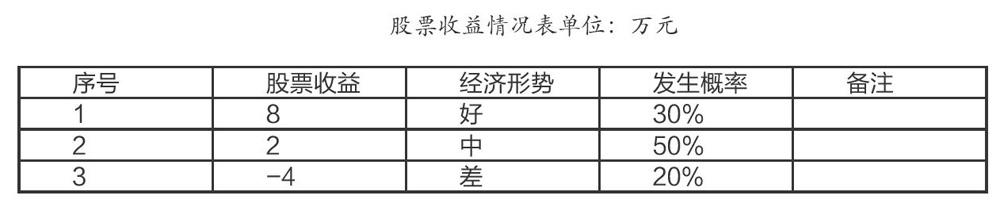
在生活当中，不管是公司或者个人，都存在可能遭遇资金盈余状况的情形，为能让这部分资金获取更优收益，常常会面临投资决策方面的问题，而这同样是需要运用到统计学领域知识的。比如说，有个人当下拥有20万元的盈余资金，要开展为期一年的投资决策，有两种投资的方案可以用来选择，一种是做股票投资pg下载麻将胡了，一种是存入银行。假定银行的利息率是10%，股票的收益状况展示在下面的表格当中：

这是三个小分句，先放这里再说哦：在依据上表的情形下，股票的收益是由经济形势的好坏来决定的，当经济形势呈现良好状态之时，对股票进行投资能够收获8万元的收益，在经济处于中等形势的状况下，投资股票可以得到2万元的收益，而当经济形势比较差时，投资股票将会出现损失4万元的情况。各种经济形势发生的概率可凭借经验获取，如此一来就能够算出投资股票的期望收益为8乘30%加2乘50%加负4乘20%等于2.6万元。把资金存放在银行能够获得的收益是20乘10%等于2万元。所以，借助比较分析能够做出决策，即把资金投入股票会更具理想性。在此要留意的是，投资股票的收益跟经济形势的优劣存在直接关联，因而在凭借经验对经济形势所发生的概率予以估计时应当遵循谨慎性原则，不然有可能致使错误的决策。

（三）统计学在抽奖方面的应用

我们生活的现实当中，抽奖活动是众多商家都乐于采用的促销办法了。一方面呢 商家靠着抽奖活动能够促使消费者留意商品还能激发消费者的购买愿望 进而达成商家薄利但多次营销多获利的目标 另一方面 消费者在选购商品的进程里由此多得到一回抽奖机遇的意思 要是中奖了 那就相当于商家在价格方面做了优惠 可让消费者获得实惠 就算没中奖 也能增加消费者的购物感受情况 然而 就是在这般的抽奖活动里面 当前实际上就运用到了统计学的相关知识 。例如，假定商家于总共500张的奖券里头设定了50张中奖奖券，这般的设定一旦达成，依统计学的相关知识能够晓得，对于即将抽奖的消费者而言，他们中奖的概率是等同的，与抽奖顺序并无关联。然而在实际生活里，有部分消费者因欠缺统计学知识，老是错误地觉得先抽奖的人中奖几率低，而后抽奖的人中奖几率高，实际上这种认识是没有科学依据的。

（四）统计学在保险行业方面的应用

在现代社会里，与任何人都有着紧密关联的保险行业，于乘坐高铁之际，得购买保险，在搭乘长途汽车之时，要买保险，于乘坐飞机的时候，需买保险，在每月工资发放之际，要交纳个人养老保险等。实际上，保险行业之所以始终存在且持续发展壮大，是将统计学的知识运用其上。比如，有两万人选购了某保险公司的人身意外保险，每人所缴纳的保费金额是 10 元，这般保费金额总计为 20 万元，若个人因故而发生意外，经核实后能够获取 2 万元的赔偿金。不过呢，2万人一块儿同时出现意外这种概率是极低极低的，极有可能出现的情形是有一小部分人出现了意外，而绝大多数的人都不会出现意外。假定这2万人里头有3个人出现了意外，保险公司就得赔付6万元的赔偿金，如此这般保险公司还能够有14万元的盈余，这实际上就是一个有关统计学的问题。所以呀，那些觉得保险公司不会盈利的人的想法是不对的，根本缘由就在于缺乏统计学方面的知识。

三、结束语

综上所述，统计学所涉及领域极为宽泛，跟我们的生活关联深切，我们当中的每一个人都得细致观察，深度体会，审慎思考，全面掌握并善用好统计学知识，以使它为我们的生活更出色地服务。虽说它没办法径直给出我们正确答案抑或最佳选择，然而它可以为我们指明方向。