pg下载赏金下载 在日常生活中,伯努利方程有哪些应用场景?
大家好pg下载渠道,今天我们来聊聊伯努利方程。
物理学以及工程学里,有个方程叫伯努利方程,它简单却极为重要,这个方程能够助力我们深入去了解广阔世界里流体的流动行为,实际上,此方程阐述了流动着的流体当中,压力、速度以及高度这三者之间的关系。

什么是伯努利方程?
,在工程领域之中,伯努利方程存在着数目极为众多的应用情况,举例来说,能够采用它去阐释飞机究竟是怎样产生升力这一现象,与之类似的,还能够运用它来计算当液体从容器内部流出之时的速度等一系列相关问题 。
在探讨这些应用之前,我们先来看看什么是伯努利方程?它是被瑞士物理学家丹尼尔伯努利在1738年给出发表的情况呢 对于该方程来说它的表达式是这样的 等式左边三项之和沿着流线有着保持不变的状态 并且它们各项的量纲全都是压力 第一项是静压 也就是在平常所说的流体压力P这种情况 第二项叫做动压 它跟流体密度ρ以及速度v是存在一种函数关系体现的 所表达的意思是单位体积流体的动能意思 第三项是静水压力 它是流体遭受重力施加影响之后因而产生的压力状况。式中g是重力加速度符号 H代表的是当前位置跟参考位置之间的高度差情况 这就是伯努利方程的压力表达式情况 当然它也能够表示成为水头形式或者是能量形式的情况 。
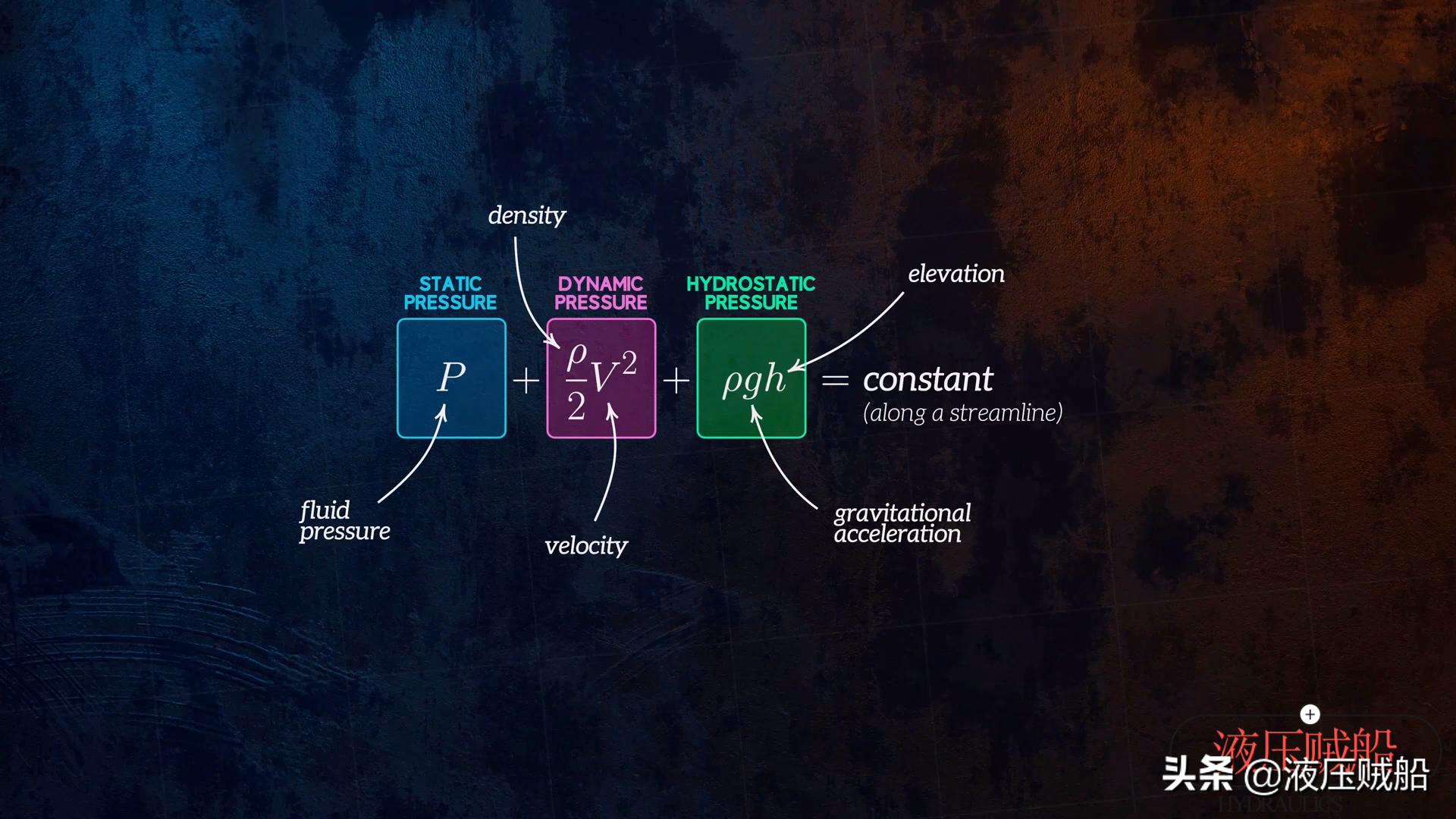
我们能够把伯努利方程视作能量守恒定律的一种表达形式,其意思阐述的是,顺着流线的前进方向,压力能、动能以及势能这三者加起来的总和是维持不变的。这属于一个极具价值的信息内容,它能够助力我们去剖析一连串流体的流动方面的问题和情况。当然需要着重说明的是,该方程仅仅能够沿着流线方向予以运用。所谓的流线,我们能够把它定义成,在处于稳态流动的状态之下,流体内部单个粒子所呈现的流动路线。更为准确地讲,它是一条在全部的点上都跟质点速度相切的曲线。

应用1——伯努利方程在变径管道中的应用
下面,我们运用伯努利方程,去瞧瞧流体流经变径管道时的情形。借助伯努利方程,我们不但能够知晓流体在流经变径管道时,压力的变动状况。而且还能够用来对不同位置处的流量情形予以比较。鉴于此,我们能够把伯努利方程转变为下面这般的形式。
紧接其后,我们选取处于同一条流线上的点1以及点2,鉴于点1与点2二者之间的高度并未呈现出显著的变化情形,我们判定它们大致是相等的,所以说势能这一项能够大致被视为相等,进而就能够相互抵消掉了。
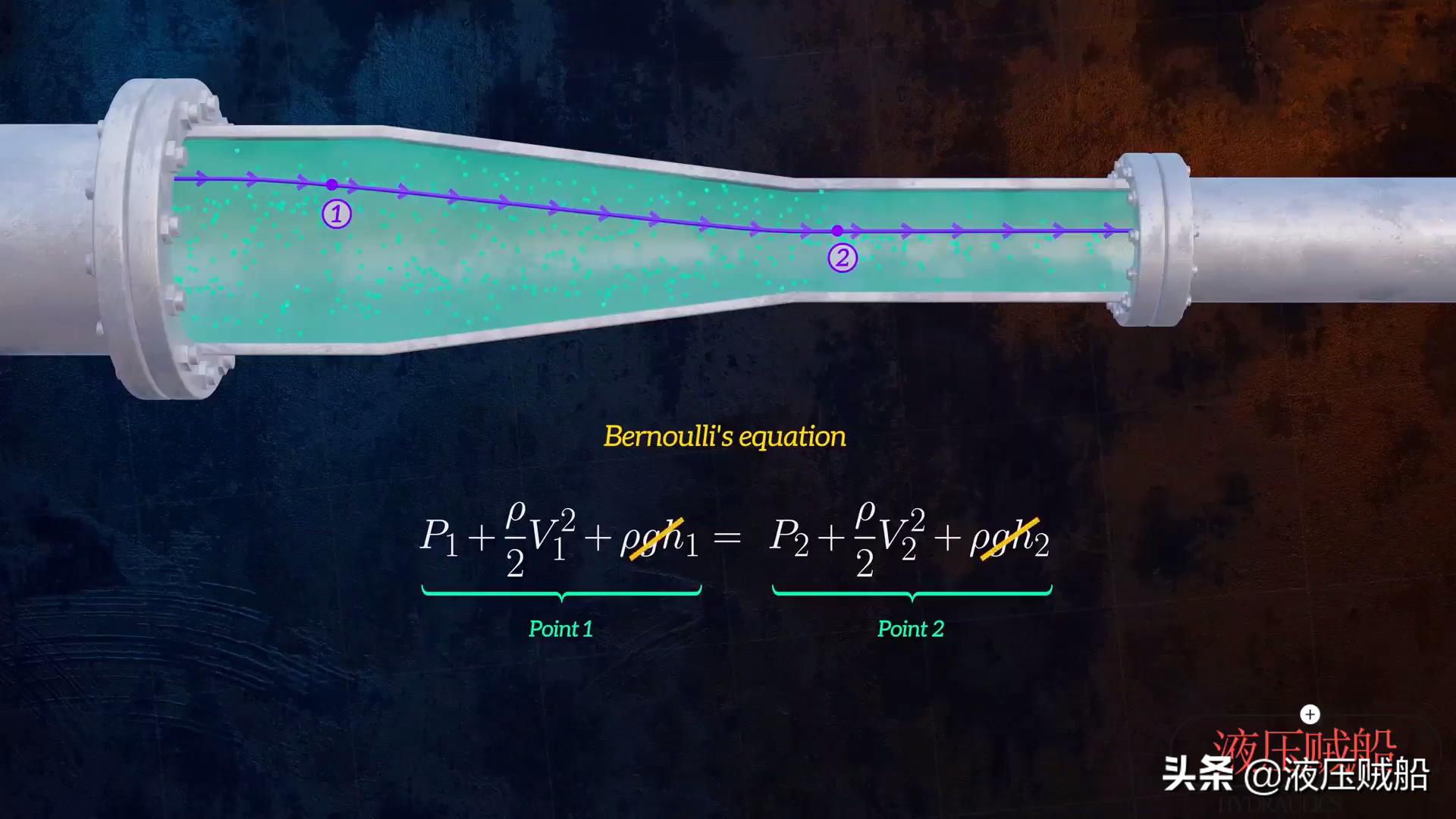
紧接着,我们将静压项统统移至等号的同一侧,如此一来便能够得到压力变化的方程。要是我们再度假定流体为不可压缩的,那么点1与点2的质量流量定然也是相等的,这便是所谓的连续性方程,它是质量守恒定律的一类表达形式。所谓质量流量等同于流体的密度、管道的截面积以及流速这三者的乘积,所以经过变换,这个连续性方程能够转变为点2的速度方程,鉴于截面积A2小于A1,这意味着流体进入直径较小的管段之际,流速会增大。
随后,我们把左侧的V2再度代入右侧的伯努利方程里,我们能够瞧见,鉴于从点1至点2,流动速度在递增,与之相反,压力却是在递减的。

一句话总结是,对于水平流动,流体速度增加必然伴随流体压力降低 ,这是伯努利原理最通俗易懂的表达 。虽说大家直觉上会认为速度增加必然导致压力增加 ,但事实并非如此 ,这一点我们还能从能量损失角度考虑 ,即流体速度增加消耗的能量都从流体静压能获取 。
应用2——飞机的升力是如何产生的?
下面,咱们借助伯努利原理,去阐释一下飞机的机翼为何竟能够从而产生升力呢,首先,我们清楚,流体流过机翼上方的流速要比流过下方的流速更快速pg下载麻将胡了A.旗舰厅进体育.cc,依据伯努利原理,这时在机翼上方就会形成低压区域,与此同时在机翼下方就形成了相对而言的高压区域,恰好是因为机翼上下两侧存在着压力差的缘由,才产生了升力。
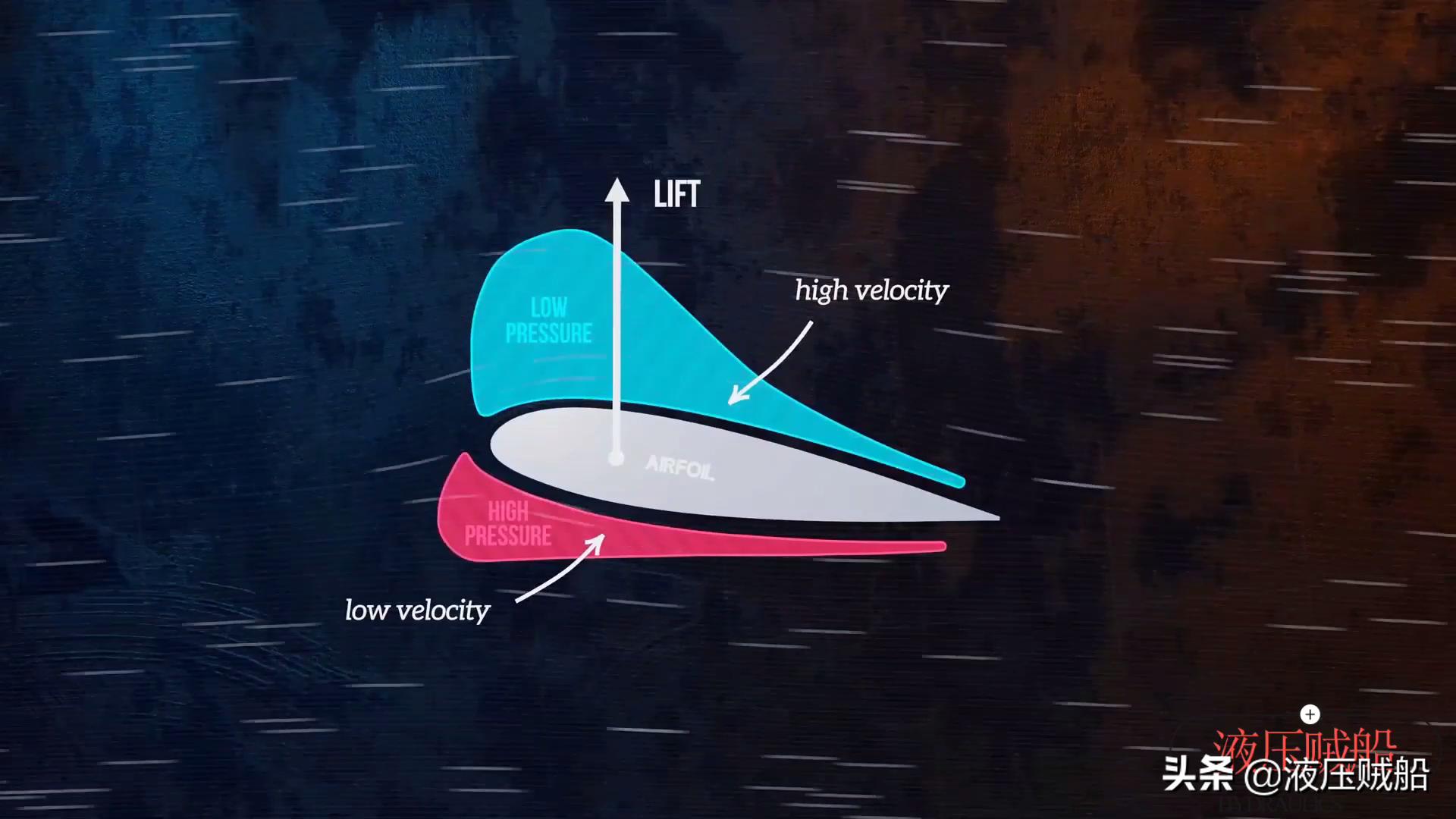
应用3——为什么本生灯能使燃气燃烧更充分?
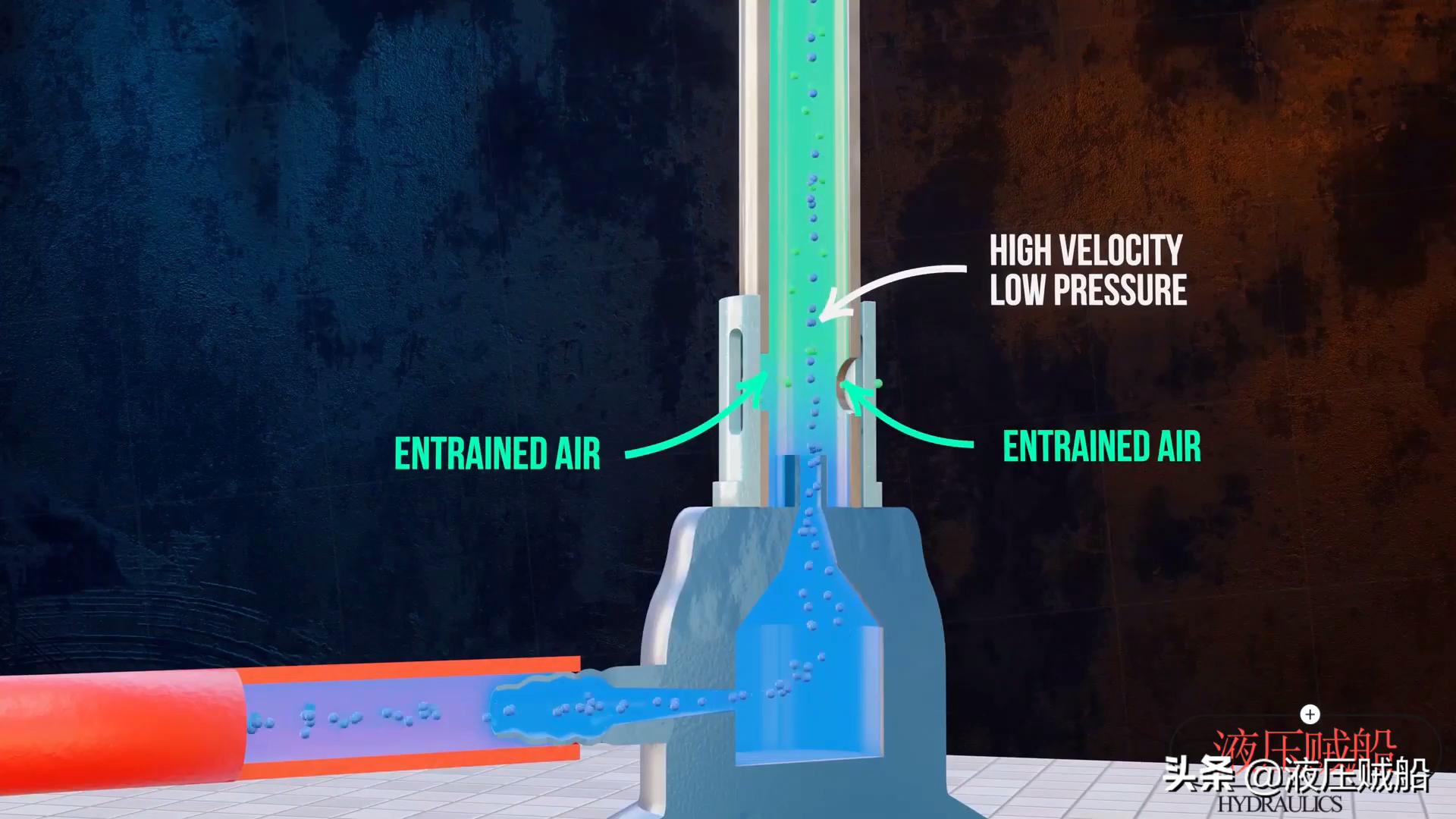
伯努利原理能够用来阐释本生灯的工作原理呀,气阀开启的时候,气体以较高速度流入灯管,依据伯努利原理,这样的高速流动会于灯管中形成一个负压区,进而致使外部的空气被强制压入灯管内,由此让空气和煤气得到更好的混合,使得燃烧更为充分。
应用4——如何利用皮托管测量飞机的飞行速度?
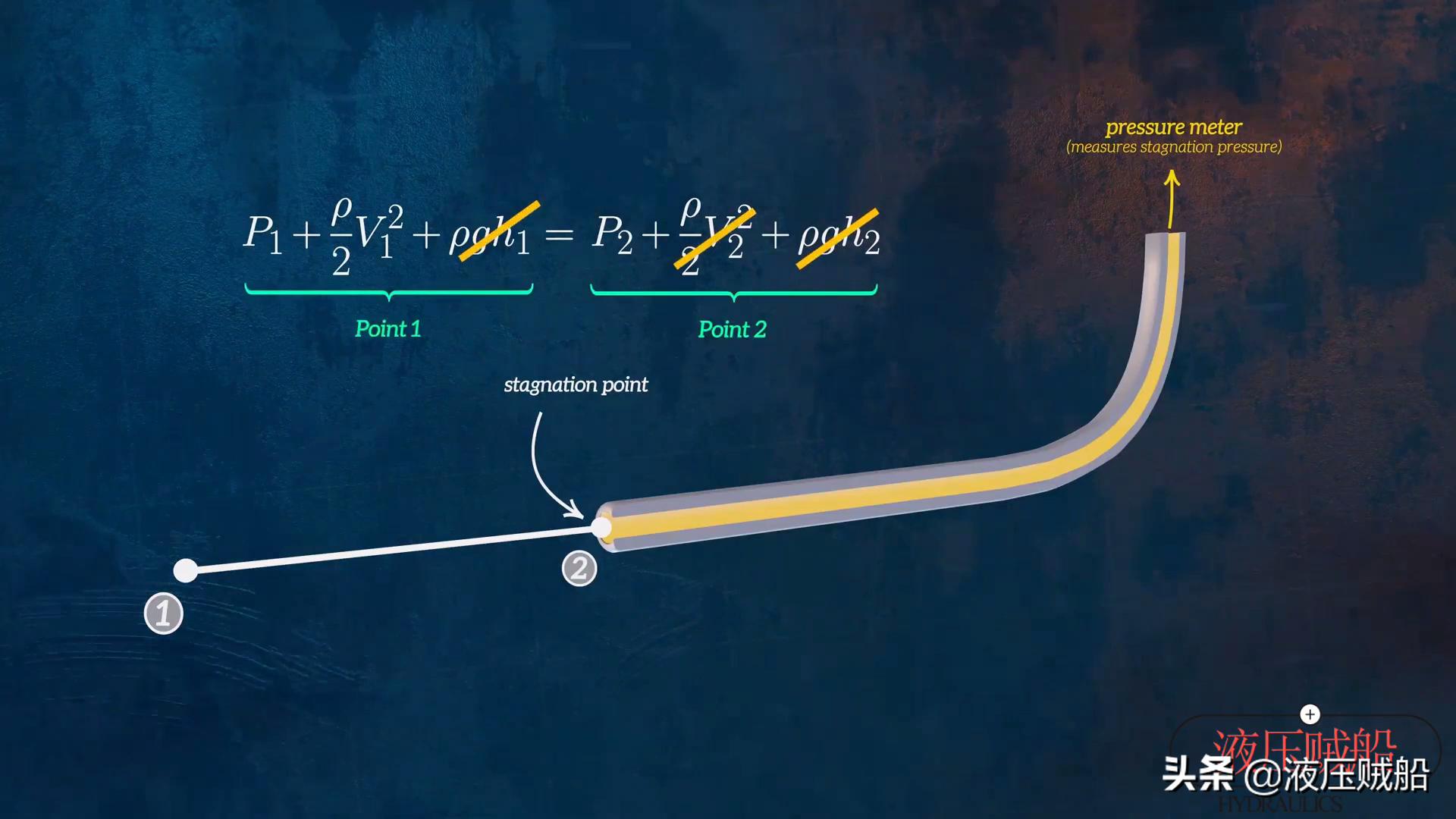
存在着一些流量计,其也是借助伯努利方程用以确定流动着的流体的速度。皮托管属于这样的一种装置,它常常被用于检测飞机的飞行速度。在这里我们对其工作原理做简单描述,要是把一根管子放置到流动的液体当中,接着在管子的末端安装一个压力计,压力仪表会检测管子末端的压力。在管子入口处流体速度为零的点,我们称作滞止点,在该点所测得的压力被称为滞止压力。我们能够于上游点1跟滞止点2之间运用伯努利方程,鉴于两点势能大致相等,并且滞止点2处的速度v2为0,所以,点2处的滞止压力等同于点1处的静压与动压之和。换而言之,点1处全部的动能基本上都在滞止点2处转变成了压力能。这时,要是我们在管子的外面再套上一根末端密封且下游开有小孔的外管,这时外管所测量的便是流体的静压力,而非滞止压力,知晓了这两个压力值,我们就能轻易地确定流速了。

应用5——文丘里流量计的工作原理?
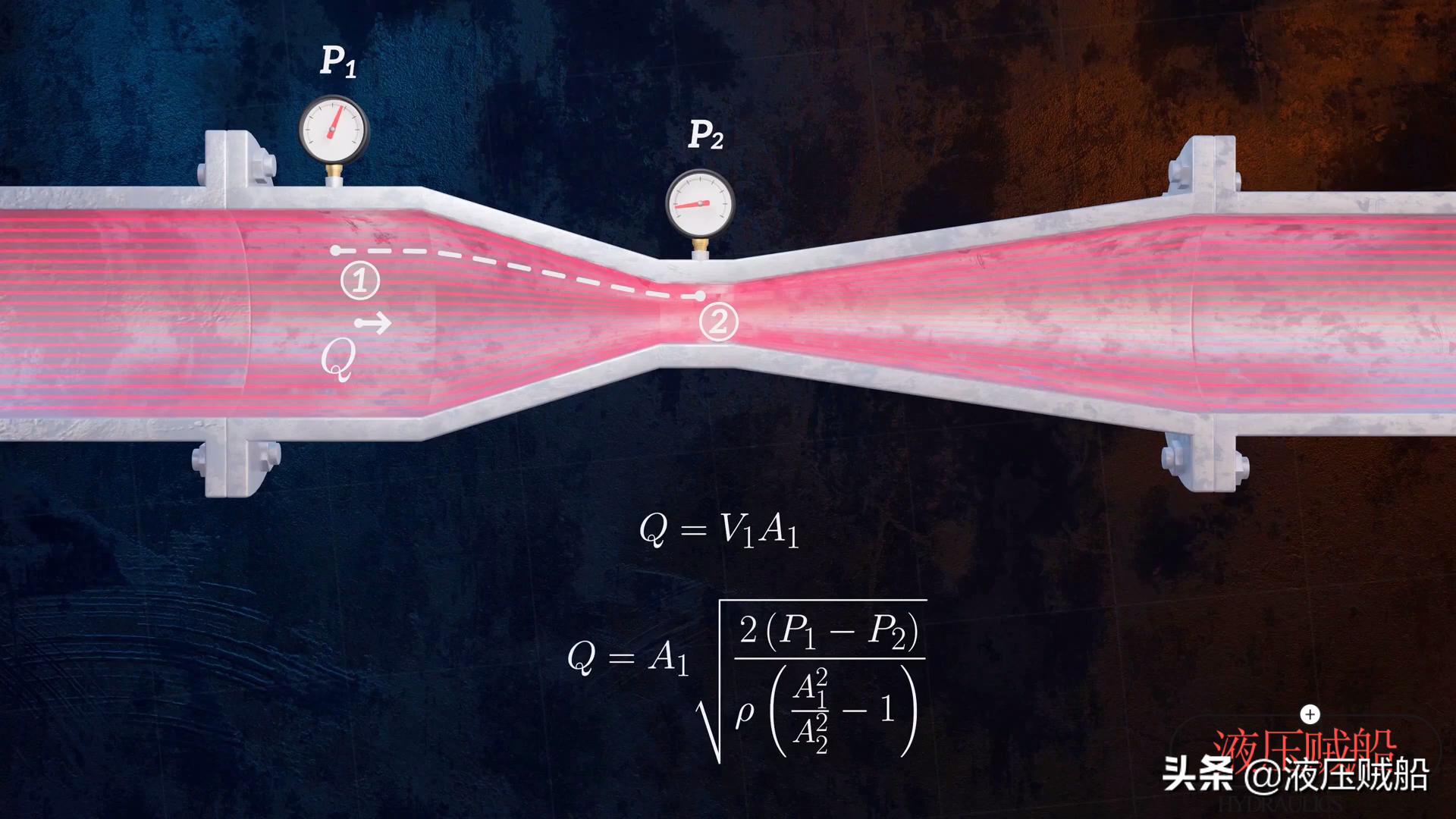
由伯努利方程制成的、用于确定管道内介质流速的、通过测量流体流过管道缩颈部位压力降来工作的另一种流量测量设备是文丘里流量计,若要确定流量Q即流速乘点1处管道截面积,可变换压降方程得到流速计算公式,接下来要做的是确定文丘里流量计尺寸、流体密度、压力P1和P2,如此流量便能计算出来了。能够检测管道流量的文丘里流量计,是一种简单可靠的设备,其内部不存在活动部件。它的扩散段长度相较于收敛段,要明显长许多,如此一来,能够显著降低能量损失。
应用6——如何计算液体从容器内流出时的速度?
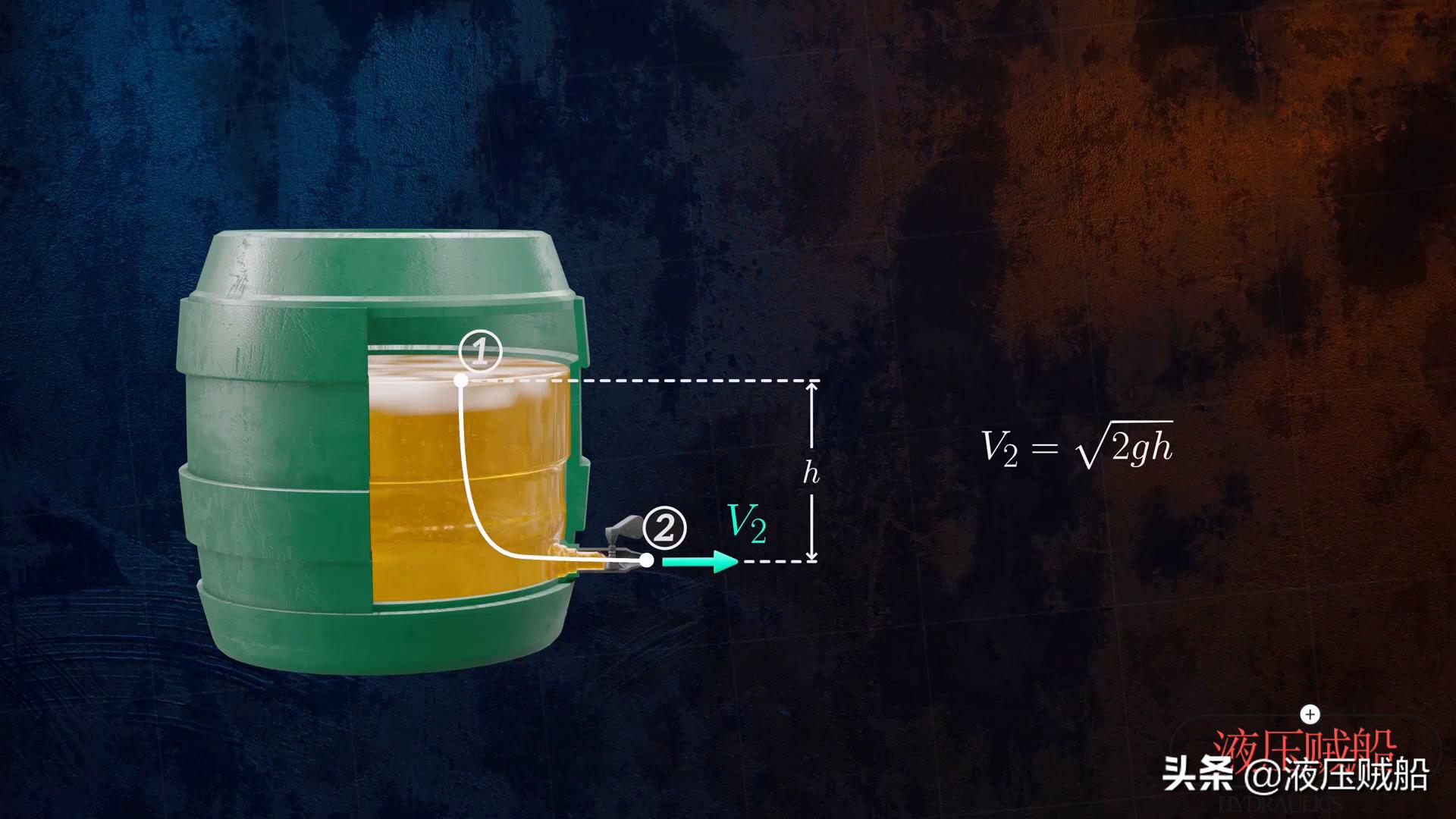
如何运用伯努利方程来计算液体从容器内流出时的速度呢?让我们接着看,假定我们有个啤酒桶,此刻要算酒桶的排空速度,首先要做的是把酒桶底部的水龙头打开,接着要在某一条流线上确定两个点,随后在这两个点上运用伯努利方程。
这个酒桶的顶部,设有呼吸口,这意味着它的顶部,是与大气相连通的,而水龙头的出口点2处,同样是与大气相通的,所以,点1和点2处的静压力,都是大气压力,能够相互抵消。另外,我们假设这个酒桶足够大,因而我们可以认为点1的流动速度,近似为0。现在pg下载官方版打开即玩v1022.速装上线体验.中国,我们变换一下伯努利方程,并且将啤酒的液位和水龙头之间的高度差,定义为H,如此便可以得到啤酒流动速度的表达式V2。
使用伯努利方程的限制条件
好了,以上这些情形均为我们生活里的例子,你同样能够试着运用伯努利方程去处理一些实际状况。然而若要达成正确运用它,那么领会其推导方式以及应用的受限之处就极为关键了。我们在此处不过多阐述其推导进程,不过必须知晓一下,在推导进程中,我们人为进行了哪些假定?这些假定会致使伯努利方程的应用范畴受到约束。
第一条假设为,流体处于流动状态时是层流情形,并且这种流动是稳态的,这表明流量不会依据时间产生改变,。
第二条假设为,流体不存在粘性,换而言之,因实际流体粘性所产生的剪切应力被忽略不计了。此假设不可或缺,鉴于流体粘性会致使流体内部出现能量损失,致使能量沿流线守恒这一结论不再适用。
第三条假设是,流体是不可压缩的,也就是说它通常只适用于液体,对于高速流动的气体可能就不适用了。
综上,想要应用伯努利方程,必须要同时满足以上三个假设。
在一定程度上,伯努利方程存在一些经过修订的版本,虽然相较于初始版本在形式上变得更为繁杂,然而却能够应用于非稳态以及可压缩流体所呈现出的流动情形。
好了,今天的内容就到这里,我们下次再见。