pg下载通道 斐波纳契数列

概述内容

数学专业界里，斐波纳契数列，也就是Fibonacci sequence，是极其有名的数列，在小说《达芬奇密码》当中，卢浮宫馆长被凶手残忍谋杀，尸体横陈于地板之上，馆长被脱光了衣物，呈现出达·芬奇名画维特鲁威人的姿态，并且还留下了一些怪异的密码，这些极难理解的密码，原来就是斐波纳契数列pg下载，它的前面几项依次是1，1，2，3，5，8，13，21，34，55，89，144·······该数列最为显著的特点便是，其中的每一项均等于它前面两项的和 。对于从第三个数开始的数，每个数同它后面那个数的比值，都极为接近0.618，此即“黄金分割” 。斐波那契数列又被称作“兔子数列”，即黄金分割数列 。这一数列看上去相当简单，却老是出现在人们的眼前 。蜻蜓的翅膀、蜂巢、菠萝表面的突起等，皆是依照这个数列进行排列的 。许多花朵的花瓣数目同样具备斐波纳契数列的排列规律，像玫瑰、菊花、向日葵等 。

斐波纳契和斐波纳契数列

中世纪的时候，西欧的经济渐渐开始繁荣起来，西方前往东方经商的商人数量逐渐增多，意大利的数学家斐波纳契便是其中之一。斐波纳契这个称呼，实际上是生活在12世纪末到13世纪上半叶的比萨的莱奥纳多的绰号，由于莱奥纳多的父亲名字叫做Guilielmo，外号是Bonacci，而Fibonacci的意思就是Bonacci的儿子。他是首个对印度和阿拉伯数学理论展开研究的欧洲人。他父亲遭比萨的一个商业团队聘请成为外交领事，派驻之地等同于如今的阿尔及利亚区域，莱昂纳多据此能够在一位阿拉伯老师的指引下钻研数学，他还在埃及、叙利亚、希腊、西西里以及普罗旺斯钻研过数学。

斐波纳契

斐波纳契于1202年所写成内容、1228年进行修订后再次出版的《算法之书》里头提出了一个相当著名的兔子相关问题 ，其大概意思是 ：要是存在一对处于幼兔阶段的兔子 ，历经生长一年后便成长为成年兔子，成长为成年兔子后的第三年开始每年都会生下一对处于幼兔阶段的兔子 ；所出生且每一对处于幼兔阶段的兔子同样会在第二年成长为成年兔子 ，成长为成年兔子的第三年开始每年又会生下一对处于幼兔阶段的兔子 ；按照这样以此类推下去 ，假设每次所生下的幼儿阶段兔子都是一只雌性兔子与一只雄性兔子 ，并且也不存在生病以及死亡的相关情况 ，如此这般从而得到的每年存栏的兔子对数 ：

给定这样一组数，其中u(1)的值是1，u(y)的值是1(y为2时)，u(3)的值为2，u(4)的值是3，u(5)被赋予的值是5，u(6)的值为8，等等，如此这般地持续。

称为斐波纳契数列。设u(0) =0，则u(k)满足递推关系

ｕ（ｋ加上二）等于ｕ（ｋ）加上ｕ（ｋ加上一），ｋ等于零，一，二，等等等等 。

以及初始条件：u(0) =0，u(1) = 1。

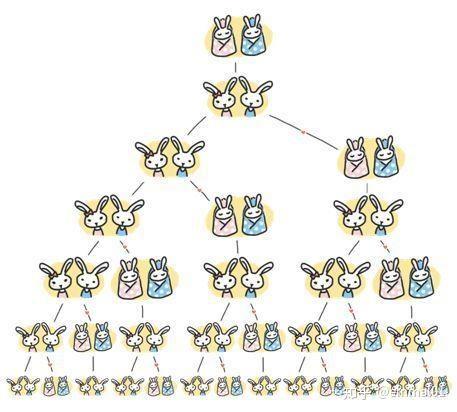
兔子和斐波纳契数列

19世纪出现了一位法国数学家，此人名为比内，处于公元1786年至1856年这个时间段，是他率先提出了斐波纳契数列的通项公式，所以将其命名为比内公式，。

比内公式自然界中的斐波纳契数列

不但兔子生育遵循斐波纳契数列规律，自然界中树枝分岔符合此数列规律，植物花瓣数目也符合该数列规律。有一位学者，一片一片数过一朵重瓣芍药花的花瓣，最后得到的结果是233瓣，233正好是斐波纳契数列中的一项。还有一位中学生物教师，采得一棵松塔，剥去鳞片数其片数，最后数得的鳞片数目是144片，这一结果仍在斐波纳契数列内。植物学家在对植物“叶序”（也就是枝、叶以及种子在植株上的排列与分布情况）展开研究的时候，发现斐波纳契数列依旧起着关键的作用。就像向日葵的花盘，从花盘中心朝着外面辐射开的对数螺线弧，将花盘划分成包含花籽的菱形小块，我们能够发觉顺时针方向延伸的螺线数目同逆时针方向延伸的螺线数目的比率，通常是13/21、21/34、34/55或者55/144。每一个比值的分子以及分母，都是斐波那契数列里相邻的两项。显然，当那比值的分子以及分母的数值越大之际，种子数量就越多，向日葵的品种相对而言也就越好。如此存在的原因颇为简单：这般的布局能够让植物的生长疏密处在得当状况下，能够最充分地去利用阳光以及空气，故而众多植物都在历经亿万年的进化进程之中演变成了如今的模样。当然，由于受到气候或者病虫害的影响，真实存在的植物往往并不具备完美的斐波纳契螺旋，是的。

向日葵的生长

雏菊、翠菊等菊科植物，其花盘具备上述特性，只因菊科植物花盘小，不易验证。不过，植物学家算出菊科植物延命菊花头状花序上两族反向螺线条数比为21/34。杉属植物球果中比值为5/8、8/13。我们观察莴头叶子、洋葱层次、松果圆锥螺线（两条反向螺线数目比为5:8）以及菠萝上瘤状物排列数目（8:13）等，能看到上述相似排列形式。

“鲁德维格定律”斐波纳契螺旋线

斐波纳契弧线又被称为“黄金螺线”pg下载麻将胡了A.旗舰厅进体育.cc，其一，该趋势线是依据两个端点来进行绘制的，比如说，从最低点反向到最高点的线上所存在的两个特定的点。其二，三条弧线都是以第二个点作为中心来绘制的，并且在趋势线的斐波纳契水平：38.2%，50%以及61.8%处有交叉。其三，斐波纳契弧线是潜在的支持点与阻力点水平价格。其四，斐波纳契弧线和斐波纳契扇形线常常会在图表当中同时被绘制出来。其五，支持点与阻力点是由这些线的交会之处得出的。要留意的是pg下载，对于弧线的交叉点而言，它会依据图表数值范围发生改变，同理，价格曲线也将因图表数值范围的不同而改换，由于弧线作为圆周的一部分，故而它形成通常保持一致。

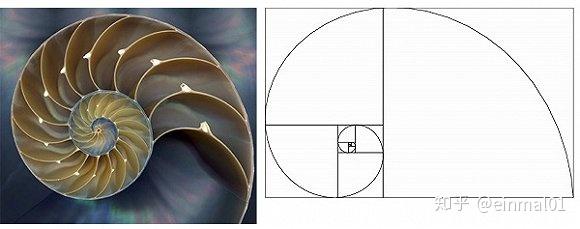
黄金螺线

在所涉及的摄影范畴之中，采取将黄金螺线予以运用的方式，能够提升拍摄出呈现出众特质的相片的可能性。与三分法这一具备静态属性的方法相比较来说，黄金螺线在我们借助眼睛去捕捉画面之际，给予了一条具备流动特性的线条。黄金螺线始终在你的两面范围以内进行旋转活动，从顶部朝着底部的方向旋转，它能够让你所拍摄画面的构图变得更加具有富于变化性。

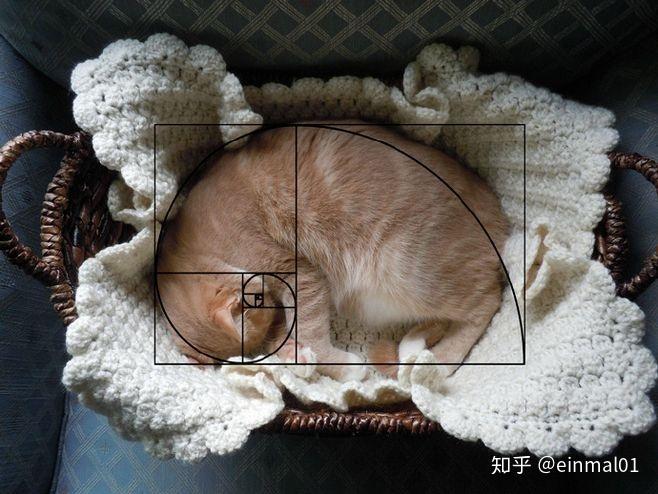
总而言之，斐波纳契数列在咱们生活里的好多地方存在着，虽说已经有不少被咱们给发现了，然而或许还有更多的有待咱们去发觉，和斐波纳契数列紧密关联的黄金比例在各个方面被运用着，可依旧有待咱们持续去探索。

参考文献：邱森所著的《线性代数探究性课题精编》，由武汉大学出版社于 2011 年出版；Keith Ball的《Strange Curves, Counting Rabbits, and other Mathematical Explorations》，由上海科技教育出版社在2011年12月5日出版第1版；郭德才，《不可思议的斐波纳契数列》发表于《发明与创新：综合版》2007年第11期，页码为24到25页；方陵生，《大自然中的斐波纳契数列之奇》刊载于《科学与文化》2004年第9期，页码为19到20页；罗文军，《数列中的一颗璀璨的明珠——斐波那契数列》发表于2017年第6期 。