卷积原理与应用

定义一组向量

，另一组向量

，那么内积可以表达为：

这即是内积，亦称为积分的累加。而投影的内涵，可以理解为向量a在基向量b方向上的分量，其具体表现为坐标值。

，这和一个点在3D欧几里得空间的三轴投影坐标是一个道理。

这样，先来看看Fourier变换在做什么：

再引入一个完美的式子开元ky888棋牌官方版开yun体育官网入口登录app，欧拉公式：

从Fourier的定义式可以看出是对f(t)和

相乘后在无穷域上对其进行积分，那么其实就是将f(t)投影在

上，如果不理解

将函数转换为两个相互垂直的三角函数，欧拉公式在此发挥了关键作用。因此，事情变得清晰起来：Fourier将f(t)映射到了两个相互正交的正弦和余弦函数构成的子空间。这一投影关系也可以通过周期信号的Fourier级数分解公式更为直观地展现出来。

阅读完傅里叶理论之后，转而探究控制论中拉普拉斯变换的应用情形：

在控制领域，阶跃信号被频繁使用，然而，遗憾的是，它并不符合狄利克雷的第三条件，因此对傅里叶变换具有免疫力。鉴于此，聪明的Laplace引入了一个衰减因子。

对信号进行衰减处理，随后执行傅里叶变换。当信号衰减至负无穷大时，衰减因子转变为递增因子。因此，Laplace变换适用于正数区域，而负数区域则可以通过系统的初始状态来描述。从这一角度来看开yunapp体育官网入口下载手机版，Laplace变换可以视为对

做了一个单边Fourier变换。

同样地，采用前述的分析方法，我们可以观察到Laplace将函数f(t)进行了映射处理。

此处所指的空间，正是s平面。相较于Fourier，其优越之处在于，它不仅能观察到虚轴上的情况，还……

的成分，还可以在实轴上看到Fourier看不到的衰减因子

这是Fourier所无法实现的。因此，Laplace在Fourier理论的基础上，进一步将信号扩展到了衰减因子的实数轴上，而这一衰减因子，

和系统的阻尼

，自然震荡角频率

密切相关，直接影响了系统的调节时间

学习过自控原理的人应当知晓，在频域部分，我们通过传递函数直接将系统的频域响应曲线转化出来，其公式为s=jw。换句话说，Fourier存在于一维的虚轴空间，而Laplace则活跃在二维的平面空间。若要获得一维空间中关于w的表达式，只需在s平面上进行降维操作即可。

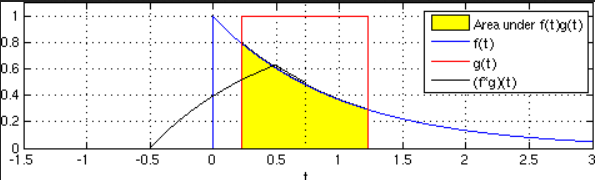
回过头来再来看看卷积投影：

这个投影有点奇怪，它在投影之前先把

执行了反对称操作，接着进行了投影处理。这一过程与之前推导出的系统卷积公式相对应。

在投影操作之前，首先对输入信号r(t)在时间轴上进行了180°的倒置处理，随后将其与系统f(t)进行叠加。对于投影这一概念，我们能够轻松把握：无论是向量间的点积运算等同于直线上的投影，还是三维空间中一个立体图形在平面上的投影，此类投影计算实际上就是两个图形重叠部分的面积。若从这一视角审视输入、系统与输出三者间的相互联系，便能够从图形学的角度阐明为何一阶系统在阶跃响应的输出中呈现为一条持续上升的曲线。为此，这里引用了wikipedia上一张关于卷积的图示进行解释，若想深入了解，读者可自行查阅相关内容：Convolution。

（特此感谢知乎学霸王尼莫的帮助）