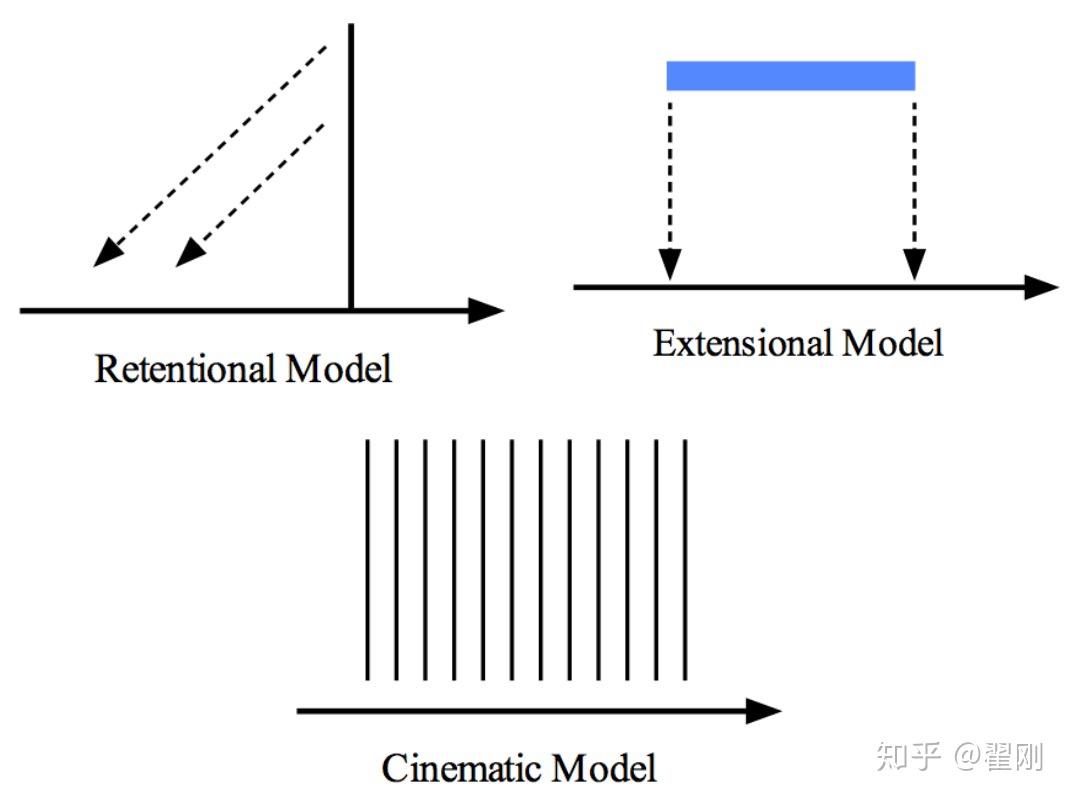
卷积神经网络——为什么卷积哪儿都能用？

两个函数的卷积

本质上就是先将一个函数翻转，然后进行滑动叠加。

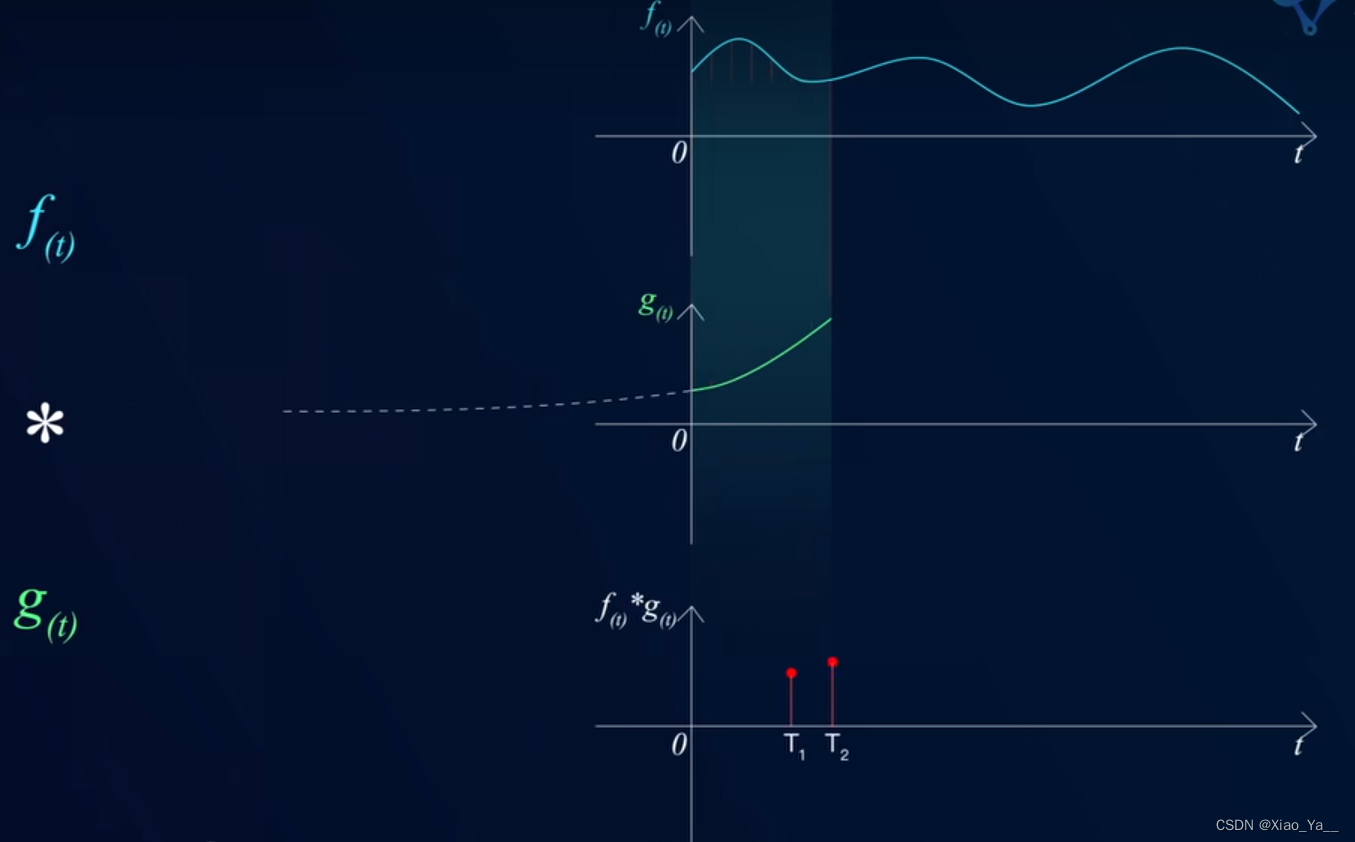
在连续情况下，叠加指的是对两个函数的乘积求积分。

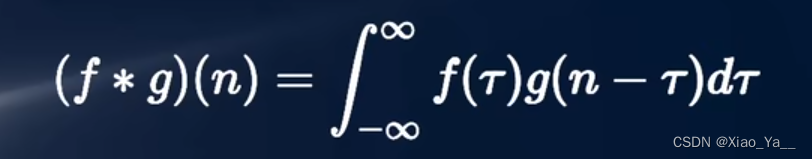
在离散情况下就是加权求和。

它在不同的领域有着不同的解释

在热力系统领域，卷积运算常被应用于对连续加入的燃料在燃烧过程中所释放出的整体热能进行计算。

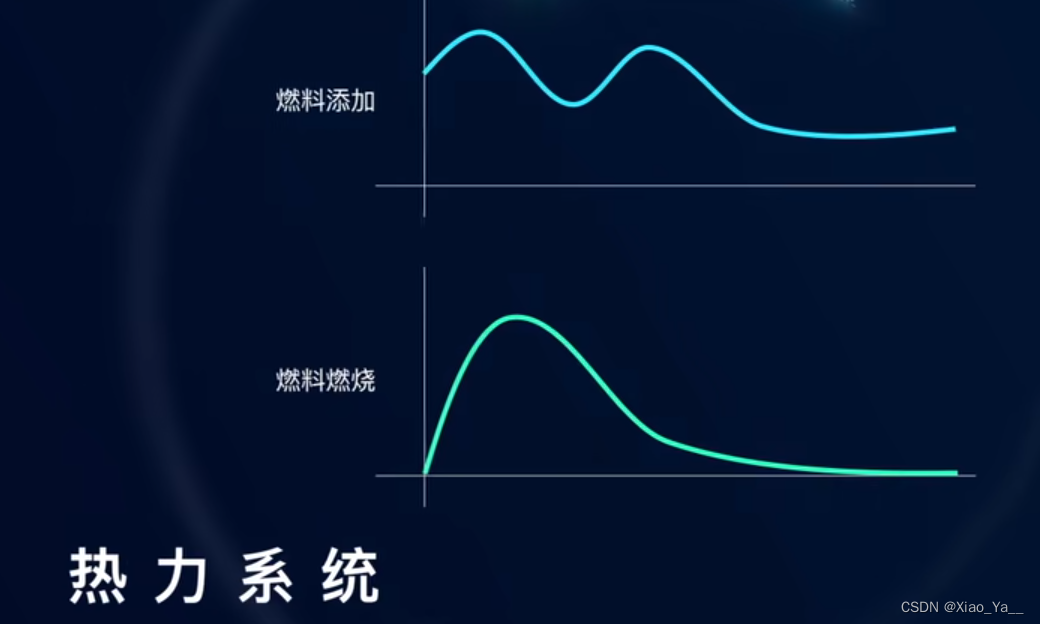
在信号处理领域，卷积运算被广泛运用，用于评估输入信号对系统所造成的累积影响。此方法能够计算出信号对系统作用的综合效果。

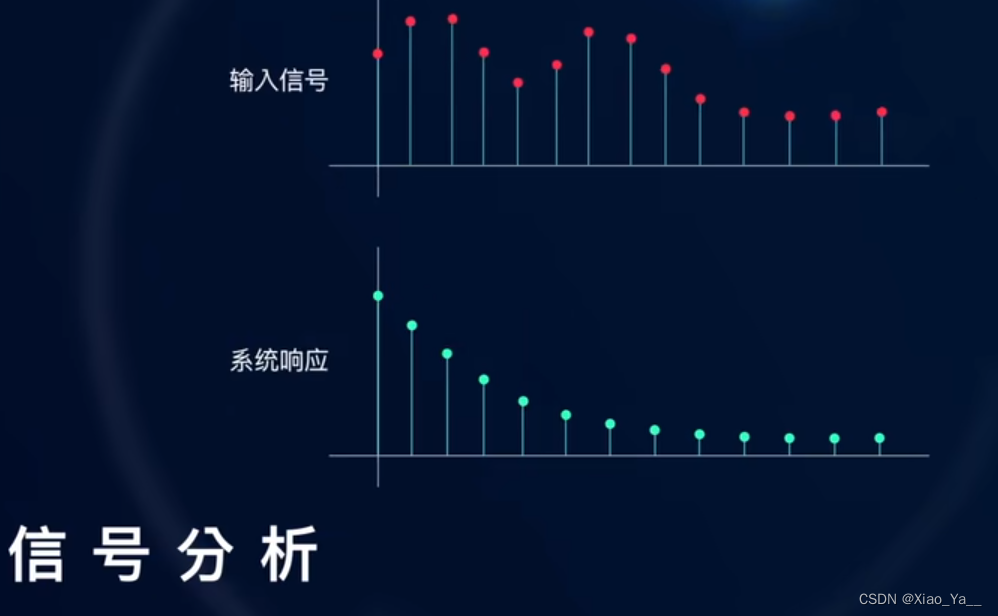
在概率论中，卷积会被用来计算二维随机变量的概率密度。

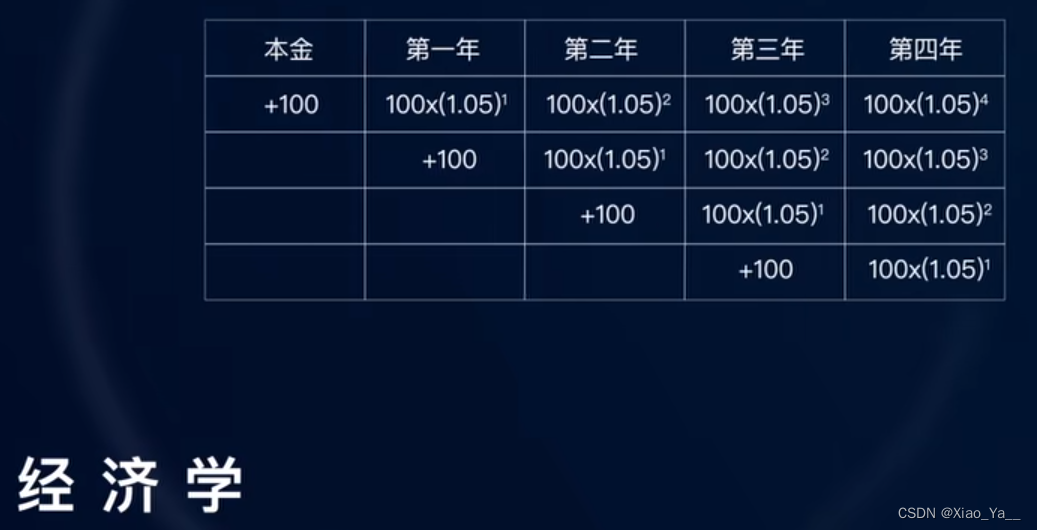
在经济学中开元ky888棋牌官方版，卷积还可以用来计算连续复利。

在机器学上的应用，卷积在数字图像处理中的有趣现象。

下面我们以3x3的卷积核为例，来阐述数字图像在计算机中是如何以三色通道的数字矩阵形式进行表示的。

进行卷积操作时，卷积核与图像对应位置相乘再求和

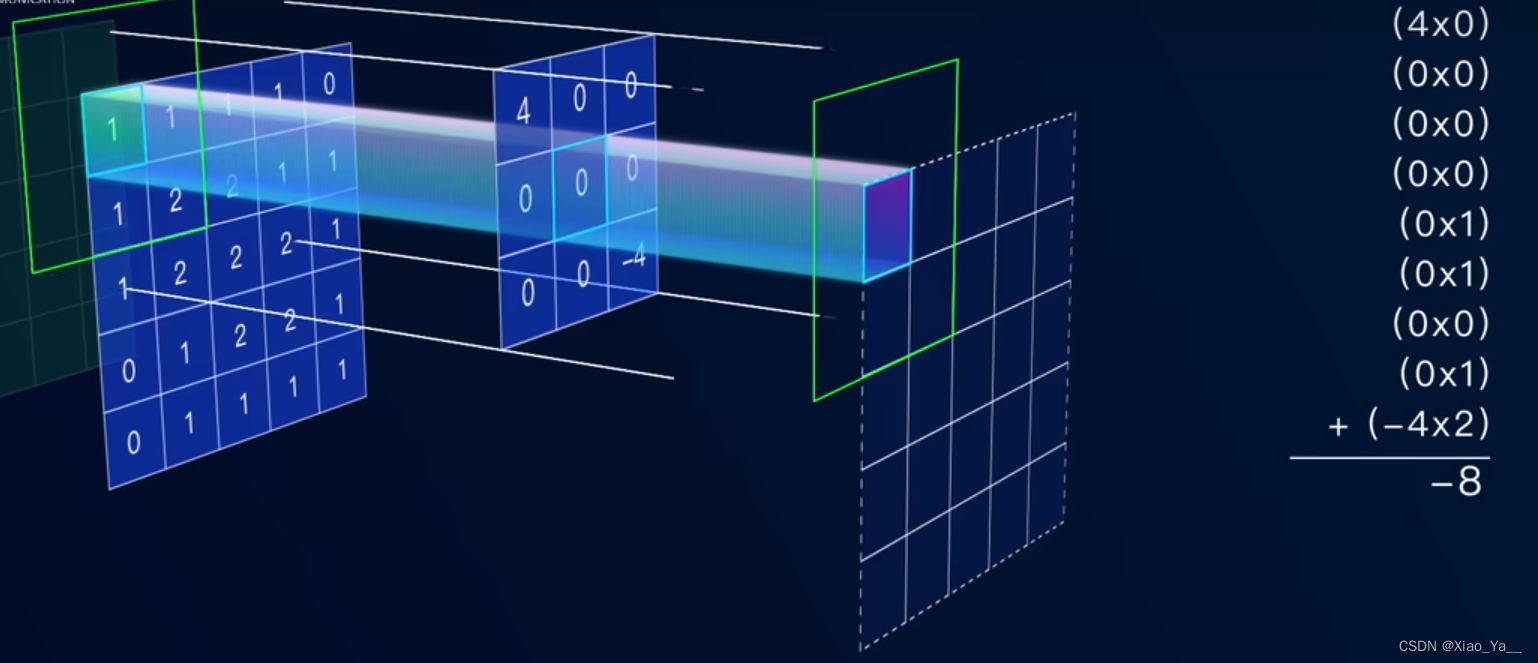
将求得的和放在被卷积操作的图中心的位置

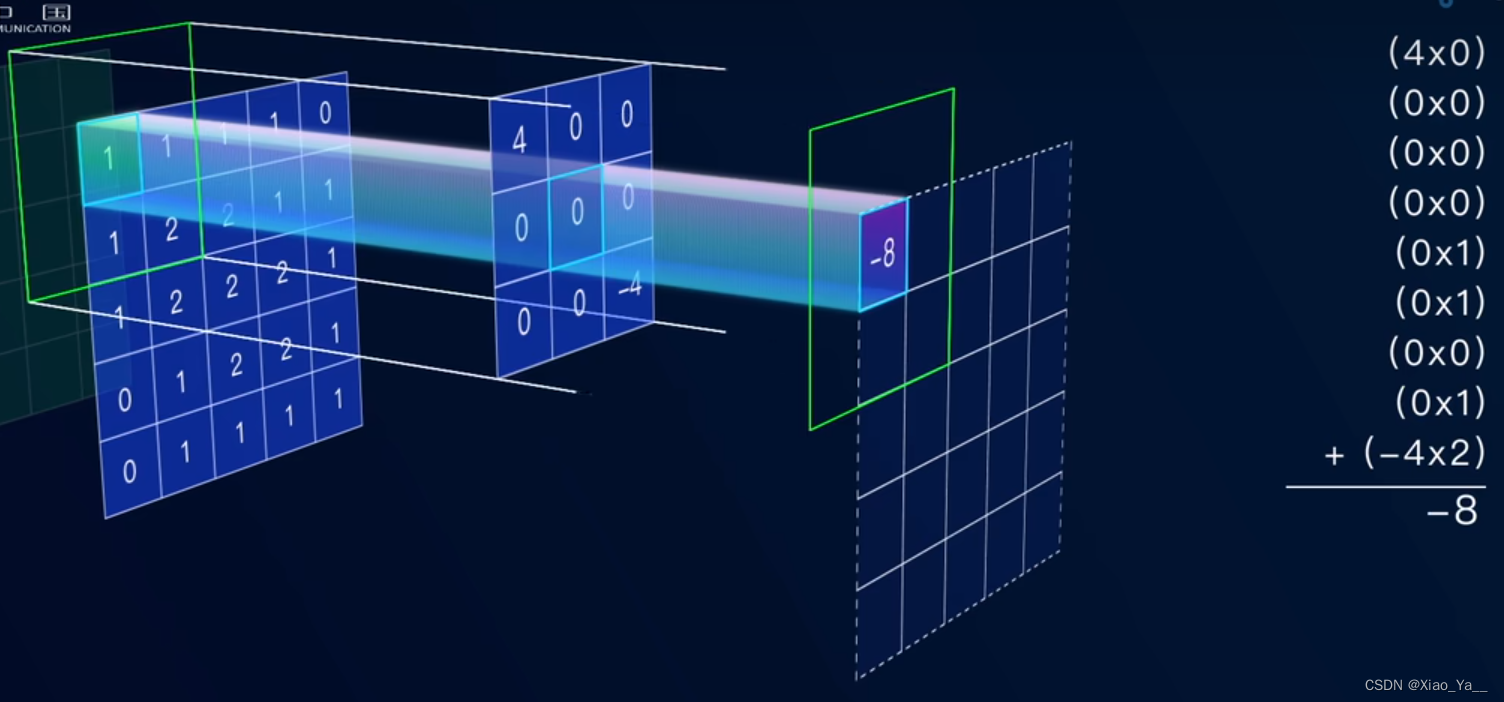
将卷积核在图像表面进行滑动，连续进行求和操作并将结果置于中心点，进而计算出图像上各个位置的卷积数值。

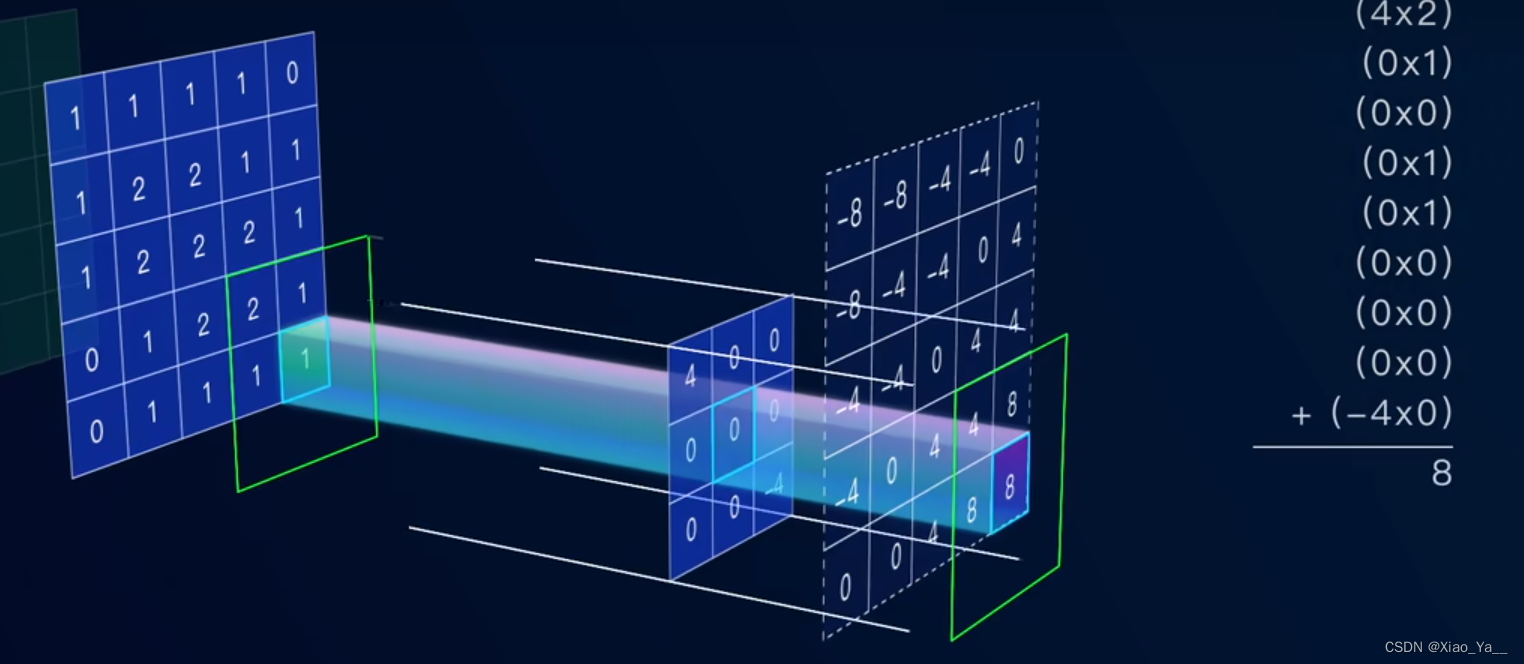
图像卷积操作在不同的卷积核下具备不同的意义

使用全部由1/9组成的3x3卷积核进行卷积运算开元棋官方正版下载，实际上等同于将中间像素的值替换为9个数值的平均值。因此，这种操作必然能够实现某种程度的图像平滑化效果。

更换一种高斯卷积核后，该核在水平和垂直两个方向上的平滑度均符合高斯分布的特征。这种核在平滑处理过程中开yunapp体育官网入口下载手机版，对中心像素的权重进行了强化，与均值滤波相比，其平滑效果更为显著。

该卷积核放大了像素周边的数值差异，从而提升了像素区域的对比度，使得图像边缘更加清晰可见，画面更加锐利，实现了图像的锐化处理。

该卷积核的卷积过程实现了图像轮廓的提取，这相当于计算了图像在水平方向上的第一阶导数。

而这个卷积核会将图像整体向一个方向平移。