大自然的隐秘技能:神奇的Fibonacci数列
科学也跨界,它总以意想不到的方式,无处不在。
在这看似单调的数列背后,蕴藏着令人惊叹的科学魅力。您若不信,不妨跟随中国科学院物理研究所的曹则贤老师,一同探寻斐波那契数列那神奇而迷人的变化过程。

自然数的数量是无限的。当我们依照某种规则将这些数字依次排列时,便形成了一个序列。这个序列可以用函数的形式来表示,即数列{an}。
如:偶数 2,4开元ky888棋牌官方版,6,8……
奇数 1,3,5,7……
三角数 1,3,6,10,15……
素数(原子) 2,3,5,7,11,13,17……
级数是指将数列中的各项通过加号连接而成的函数。傅里叶级数技术,源自傅里叶级数,是数学和物理领域极为强大的工具。您可能难以置信,但将成本征函数展开成级数,正是量子力学中的基础操作。

在人类漫长的历史长河中,意大利的数学奇才斐波那契(Leonardo Fibonacci)以其卓越的才华著称。在他年轻时期,他跟随父亲远赴北非从事商业活动,期间有幸接触并学习了阿拉伯数字。到了1202年,斐波那契创作了《Liber Abaci(算书)》这部著作,将印度-阿拉伯的数字系统介绍给了西方世界。
阿拉伯数字的引入使得数学和物理学的蓬勃发展成为可能。这两门学科广泛采用阿拉伯数字以及拉丁和希腊字母进行表述,这已成为所有追求科学研究的人们必须精通的一整套学术语言。
在《算书》这部著作中,斐波那契提出了一个引人入胜的问题:设想有一对成熟的兔子,它们每过一个月就能繁殖出一对新兔子,而这新兔子同样在一个月后便成长为能够生育的成年兔子。如此循环往复,若每对兔子都能持续经历生育、成熟以及繁殖的过程而不死亡,那么在N个月后,会有多少对兔子存在呢?为了更直观地理解这个问题,我们可以通过绘制一棵树状图来展示。
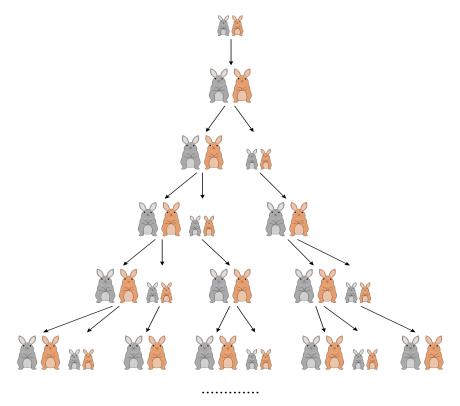
这个数列可以写作:1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144……,序列中的每个数字都称作斐波那契数,并标记为Fn。其中,F(0)等于1,F(1)也等于1,而对于n大于等于2的自然数n开yun体育app入口登录,F(n)的值等于F(n-1)与F(n-2)的和。
这便是广为人知的斐波那契数列,亦被称作“兔子数列”。
尽管颇具趣味开yunapp体育官网入口下载手机版,然而,这究竟有何价值?斐波那契数列究竟对人类的进步有何重大影响?
数学和物理领域的每个研究对象都隐藏着众多我们尚未知晓,或是即便知晓却难以领悟的奥秘。这些奥秘对我们而言难以捉摸,然而科学家们却能深入其中,洞悉其理。
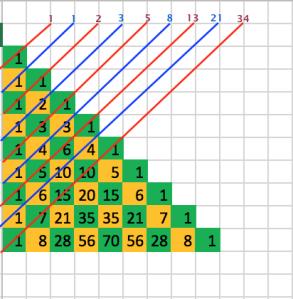
在数学领域,杨辉三角形这一结构,它由一系列二项式系数构成,广泛出现在概率论、组合学和代数等学科中。它与斐波那契数列之间存在密切联系,具体表现为:杨辉三角形中各对角线上的数字相加,结果恰好对应斐波那契数列的数值,如图例所示。
1611年,被誉为天文学巨匠的开普勒,在其著作《Strena seu de Nive Sexangula (六角雪花)》中明确阐述:斐波那契数列趋向于黄金分割比率。
随着数列的无限增大,斐波那契数列中的各项数值之比将逐渐逼近一个特定的比值,这个比值就是著名的黄金分割比,其数值为1.618033987498948482……。
黄金分割比例中蕴含着深奥的奥秘。在数学运算和物理探究的过程中,人们常常会不经意间发现黄金分割比例的身影。
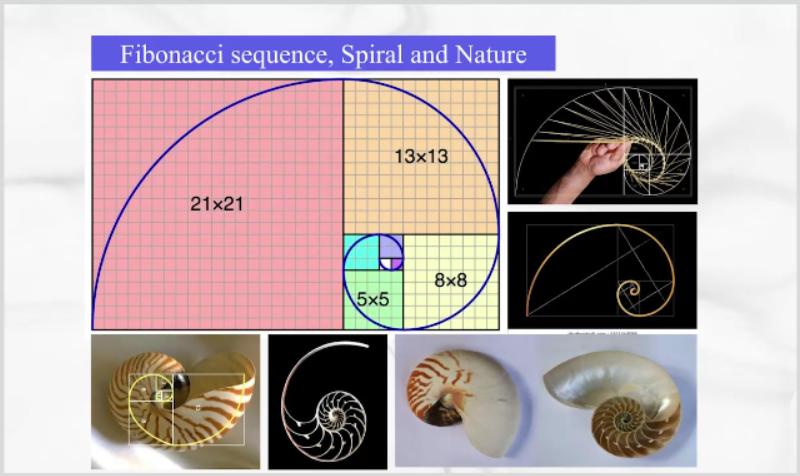
依照斐波那契数列的规则,选取边长依次为1、1、2、3、5、8、13、21等的一系列正方形,以这些正方形的一个顶点为圆心绘制四分之一的弧线,接着将所有弧线连接起来,最终形成的螺旋图形即为我们所见的“斐波那契螺旋线”。
黄金分割之数构成了美学理论的核心。在建筑设计与艺术雕塑中,人们广泛运用这一比例。自古以来,众多神秘建筑均以黄金分割为设计准则,例如金字塔的斜面三角形,其高与底面半边长的比例便遵循此规律。维纳斯雕塑堪称黄金分割之美的典范。即便艺术家无需精通数学,但若不掌握黄金分割之数,便难以称得上是一位合格的艺术家。

各个领域中,斐波那契数列的身影屡见不鲜。在日常生活里,斐波那契数列的运用尤为突出,尤其是在植物学领域。人们在观察自然界时注意到,树木在生长过程中会形成枝条,若从底部向上逐一计数这些枝条,会发现它们的数量依次为1、1、2、3、5、8、13……,这正是斐波那契数列的排列顺序。自然界中各色花朵各具其独特的魅力,然而,绝大多数花朵的花瓣数量却倾向于遵循斐波那契数列的规律,比如3片、5片、8片、13片……
植物学领域中的叶序现象与斐波那契数列高度吻合。叶序学是一门专注于探究植物器官排列规律的学科。植物的叶片以螺旋状的方式向上生长,众多植物的叶序周期普遍遵循斐波那契数列的排列模式。

在植物学领域,斐波那契螺旋排列现象同样普遍存在。这种螺旋排列既可以被视为一种向左旋转的螺旋形态,亦可以被视为一种向右旋转的螺旋形态。在这两种不同旋转方向的情况下,螺旋的数量恰好对应着斐波那契数列中相邻的两个数字。诸如向日葵的花盘、松果的种子以及菠萝的叶片等,都完美地体现了这一特性。
科学家们提出,斐波那契螺旋线在圆锥表面形成了一种相同单元的紧密排列,这种结构对植物种子的堆积和后代的繁衍大有裨益。因此,自然界中充满了无尽的奥秘,我们需要用数学和物理的视角去探索它。对自然奥秘的洞察,是对自然的一种崇高赞美。

历经千载,斐波那契数列的神奇特性不断得到证实,其应用范围已拓展至计算机科学、物理学以及化学等多个学科,使得这一古老的数列重获生机,焕发出新的活力。
在计算机编程领域,众多C语言教材在介绍递归函数时,斐波那契数列常被用作教学实例。此外,斐波那契数列也是从小学至大学不同教育阶段数学课程的重要内容之一。
在当代物理学领域,通过斐波那契数列,我们能够推导出黄金分割、白银分割以及白金分割在三维物理空间中的准周期性。而在量子力学中,研究两粒子纠缠状态和量子临界点同样与斐波那契数列密切相关。
在化学界,应力工程技术被用于重现无机材料中斐波那契数列形成的斜向螺旋之美。此外,斐波那契数列在股市分析中也得到了广泛应用,它能够揭示股价波动的深层次规律……
中国下一代教育基金会、深圳市平安公益基金会与科技日报社共同策划制作了“神奇的Fibonacci数列”科普视频系列,目的是引导青少年在大自然中寻找数学的奥妙,通过学科学习培育他们的科学态度,同时激发他们探索科学的兴趣和创新的思维。
《科技日报》矩阵号、中国科技网、科普中国、腾讯视频、西瓜视频、B站、百度百家号、微博泛知识以及青少年科技素养提升计划公众号等多个平台,将于2022年2月23日同步推出本系列视频内容。敬请关注我们,以便获取更多关于神奇数列的详细信息。(赵卫华)