深度学习：一文读懂

[id_675592545]

本文梳理了深度学习里几种常见的卷积方式，并打算用一种简单易懂的方法来阐述它们。望能对你掌握知识有所助益。

这篇文章源自于机器学习杂货店的公众号平台，系火龙果软件Linda负责编辑，并加以推荐。

卷积在深度学习领域具有关键作用，但深度学习中的卷积具体指什么，又包含哪些类型，可能并非所有人都清楚。近期，研究者Kunlun Bai撰写了一篇关于深度学习卷积的论文，以简洁明了的语言阐释了深度学习涉及的不同卷积及其特点。由于原文篇幅较长，机器之心仅挑选了部分内容进行分享，具体可参考第2、4、5、9、11、12节。

若你听闻深度学习里各类卷积的区分，诸如二维三维一维单通道转置扩张空间可分深度可分展平分组混洗分组卷积，却对其确切含义感到困惑，那么这篇文章正是为你准备的，能够协助你明晰它们实际运作的机制。

本文旨在梳理深度学习里几种典型的卷积操作，并尝试以通俗易懂的方法阐述其原理。

愿此篇文章能助你建立对卷积的清晰理解，同时也可作为你钻研或掌握相关知识时的得力助手。

一、卷积与互相关

卷积在信号分析、图像分析以及众多工程与科学分支中应用普遍。深度学习中的卷积神经网络，其结构命名便源于此技术。然而深度学习范畴内的卷积，实质上是信号或图像处理领域中的相关运算。这两种运算手法间存有细微不同。

不必过于钻研细枝末节，我们即可察觉出这种差异。信号或图像处理范畴内，卷积的界定如下：

它的解释是，通过把一个函数翻转，再进行平移，接着与另一个函数相乘，最后对所得结果进行积分运算。接下来的图形，能够说明这个概念。

信号处理领域涉及卷积运算，过滤器 g 需要先进行翻转处理，接着沿着水平方向移动。每当过滤器到达某个位置时，要计算 f 与翻转后的 g 相重合部分的面积总和。这个面积总和即为该特定位置上的卷积结果。

此处，g 充当筛选器角色。将其翻转后，再水平移动。每移动一个点，都算出 f 与翻转 g 重叠部分的宽。这个重叠宽度就是该点的卷积结果。

另一方面，互相关是两个函数间的滑动点积或滑动内积运算。互相关中的过滤器无需翻转，直接在函数f上移动。f与g的相互重叠部分就是互相关。下图对比了卷积运算和互相关运算的不同之处。

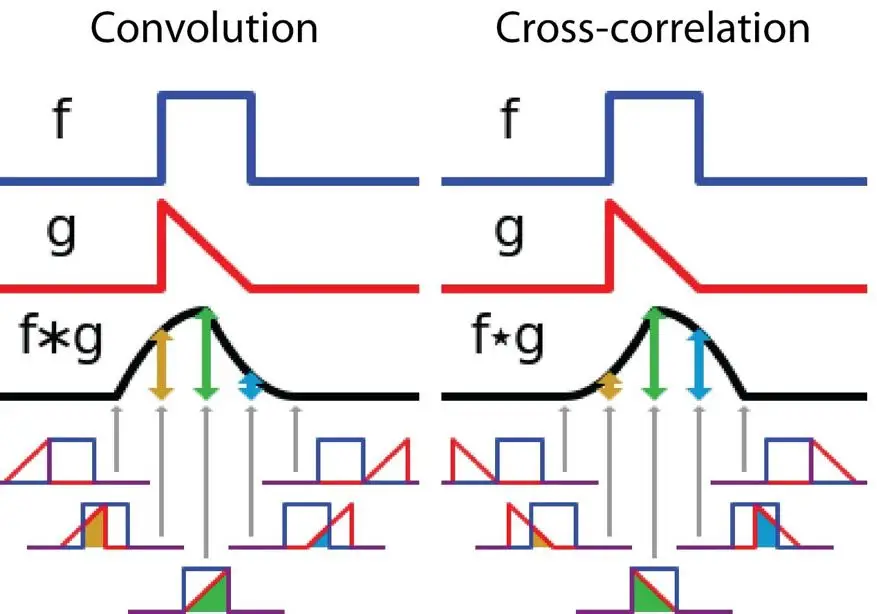
信号处理中卷积与互相关之间的差异

深度学习里，卷积操作中的滤波器不会翻转过来。准确点说，这是互相关运算。我们实际进行的是元素对元素的乘积和求和。不过深度学习领域，直接叫它卷积更方便些。这完全可以，因为滤波器的权重是在训练过程中掌握的。假如例子中那个反转函数g确实是对的，那么经过训练，掌握的滤波器就会像g函数翻转后的样子。所以，训练过程无需像实际卷积那样，把滤波器先翻转过来。

二、3D 卷积

先前章节说明，我们实际是对三维体素实施卷积运算，不过一般情形下，深度学习领域仍称其为二维卷积，具体是指对三维体素数据执行二维卷积，滤波器深度值同输入层深度值相同，该三维滤波器仅沿两个维度位移（即图像的高度与宽度方向），此操作结果生成一张二维图像，且仅含一个通道。

三维卷积确实是一种存在，它本质上是二维卷积的拓展形式。具体来说，三维卷积的过滤器深度要小于输入层的深度，这个比例关系可以用核尺寸大于输入层数来表示。当过滤器尺寸为3×3时，这种情况下，空间可分卷积的计算量会减少，相对于标准卷积来说，其计算成本只有三分之二。当过滤器的尺寸是 5×5，这个比例就是 2/5；而一旦过滤器的尺寸变成 7×7，这个比例就变成了 2/7。

空间可分卷积确实能降低开销，不过深度学习领域却很少采用这种方法。一个核心症结在于并非每个卷积核都能拆分成两个更小的核。倘若完全用空间可分卷积替代常规卷积，那么在训练时会限制搜索所有潜在卷积核的能力。这种做法可能导致最终的训练效果不够理想。

2、深度可分卷积

现在来分析深度可分卷积，这种技术在深度学习领域应用更频繁，例如在 MobileNet 和 Xception 模型中都能见到。深度可分卷积实际上由两个环节构成，首先是进行1×1 的深度卷积核处理，然后是另一个步骤。

先简单重述一下先前讲过的二维卷积核一维卷积的内容,再开始介绍这些步骤。先快速回顾一下常规的二维卷积操作。举个例子,假如输入层尺寸为7×7×3(高×宽×通道数),过滤器尺寸为3×3×3。执行一次二维卷积操作后,输出层尺寸变为5×5×1(只有一个通道)。

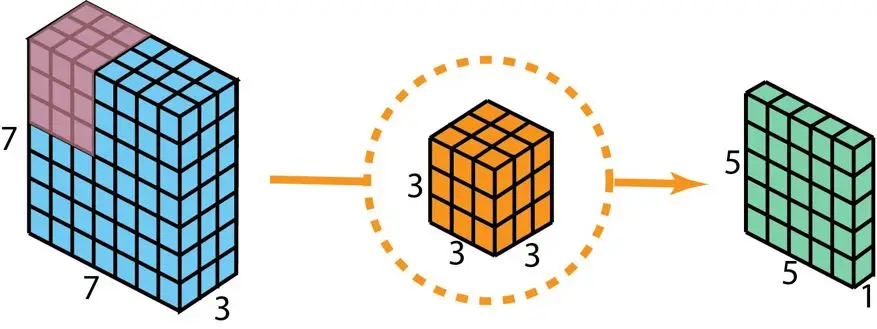
创建单层输出的标准二维卷积，仅需一个滤波器

通常情况下，多个筛选装置会置于两个神经网络单元之间运作。设想当前部署了128套筛选装置。经过这128套二维卷积处理后，会得到128张5×5×1的映射图像。接着将这些映射图像叠放组合，便构成一个5×5×128的单一层结构。运用这个方法，输入端（7×7×3）能够转变为输出端（5×5×128）。高度和宽度两个空间维度会收缩，而层次深度则会扩充。

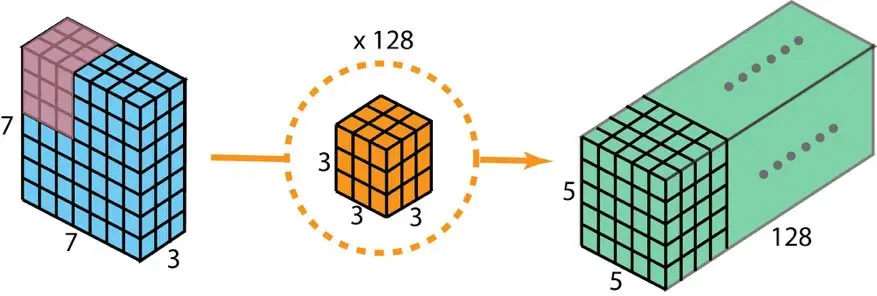
构建具备 128 层输出的常规二维卷积核，需要配置 128 个滤波器

现在使用深度可分卷积，看看我们如何实现同样的变换。

我们首先把深度卷积施加到输入层面。不过，我们不用单个3×3×3尺寸的过滤器，而是分开用3个核。每个核的尺寸是3×3×1。每个核只和输入层的一个通道做卷积（注意开yunapp体育官网入口下载手机版，不是所有通道）。这样的卷积能产生5×5×1尺寸的映射图。接着把那些对应关系图叠放组合，形成一个 5×5×3 的图形。这样处理后，便得到一个 5×5×3 的结果。此时可以减少空间中的维度数，不过层叠的层数维持原状。

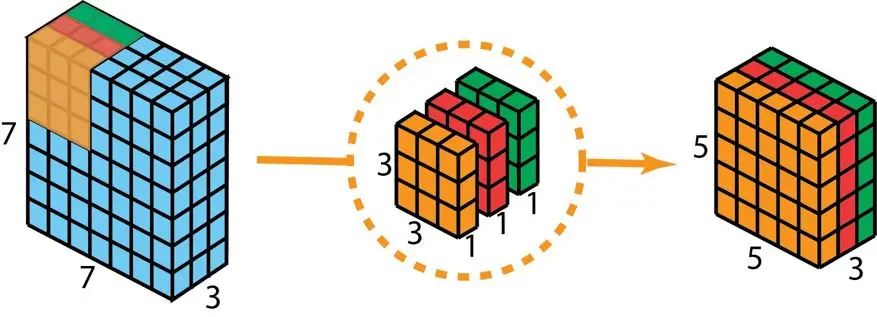
深度可分卷积初始阶段，我们摒弃传统二维卷积里单一3×3×3的滤波器，改用三个独立核进行操作。每个核的规格为3×3×1。单个核仅与输入层的一个特定通道执行卷积运算，注意不是同时对所有通道处理。通过这种独立处理方式，每个核都能生成一张5×5×1的映射图结果接着把那些对应关系图叠放起来，便构成一个 5×5×3 的图形，通过这个步骤，我们获得一个 5×5×3 的结果。

在深度可分卷积的后续步骤中，为了增加层数，我们运用了一种尺寸为 1×1×3 的 1×1 卷积层。把 5×5×3 的原始图像数据，和每一个 1×1×3 的卷积核进行运算，从而产生一个 5×5×1 的特征分布图。

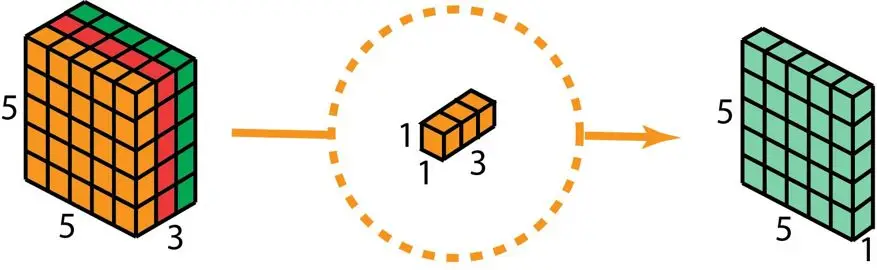
因此，经过 128 次运用 1×1 的卷积操作，我们便产生了一个体积为 5×5×128 的层级结构。

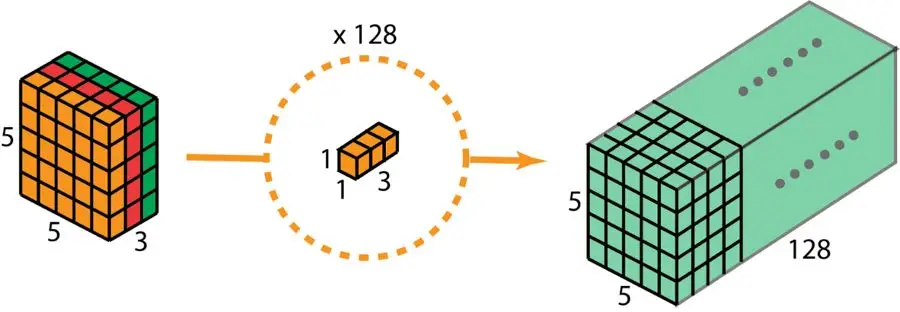
深度可分卷积——第二步：应用多个 1×1 卷积来修改深度。

运用这两项操作，深度可分卷积能够把原始的输入数据从7×7×3的维度调整成5×5×128的形态。

下图展示了深度可分卷积的整个过程。

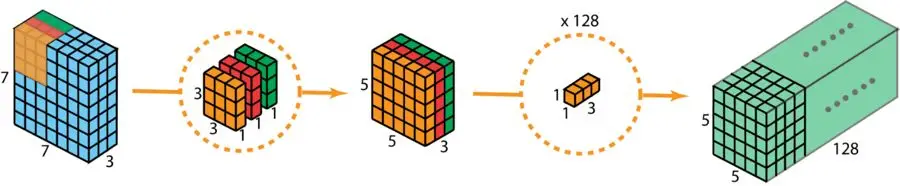
深度可分卷积的整个过程

因此，深度可分卷积有什么好处呢？主要是效率高，与二维卷积相比，深度可分卷积需要的运算量要小很多。

回想我们先前那个二维卷积的案例，需要多少计算量。总共动用了128个尺寸为3×3×3的滤波器，每个都执行了5×5次运算，这意味着需要进行128乘以3乘以3乘以3乘以5乘以5次乘法，合计达到了86400次。

分卷积又怎样呢？在首个深度卷积环节，涉及 3 个 3×3×1 的核，每核在 5×5 区域内滑动开元ky888棋牌官方版，共计进行 675 次乘法运算。而在 1×1 卷积的后续阶段，有 128 个 1×1×3 的核，同样在 5×5 区域内移动，总共执行了 9600 次乘法计算。因此，深度可分卷积总共涉及 675 次乘法，另外还有 9600 次乘法，二者相加得到 10275 次乘法运算，这个运算量相对于 2D 卷积来说非常小，大约只有其 12% 的规模。

因此开yun体育官网入口登录app，针对任何尺寸的图形，当我们运用深度可分卷积时，具体能够节省多少时间呢？让我们将之前的案例进行推广。当前，对于规格为H×W×D的输入图形，倘若采用Nc个尺度为h×h×D的滤波器执行二维卷积（其步长为1，边界填充为0，并且h为偶数），完成该转换过程所需要的全部乘法次数总计为：输入数据的维度是高宽深度相乘的积，输出数据的维度是高减去核高加一乘以宽减去核宽加一乘以类别数，将前者变换为后者需要进行大量的乘法运算，具体次数为两者相乘的结果，即输入层的高宽深度乘以输出层的高宽类别数

Nc个h高的h宽的D深度的小块，每块有H-h+1行W-h+1列

另一方面，对于同样的变换，深度可分卷积所需的乘法次数为：

D乘以h乘以h乘以1乘以H减去h加1乘以W减去h加1,再加上Nc乘以1乘以1乘以D乘以H减去h加1乘以W减去h加1,等于h乘以h加上Nc乘以D乘以H减去h加1乘以W减去h加1

则深度可分卷积与 2D 卷积所需的乘法次数比为：

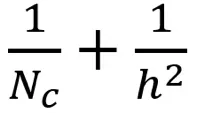
当前多数设计中的输出单元往往包含大量路径，数量能达数百乃至上千个。针对这种结构（Nc远大于h），相关公式可以简化为1除以h的平方。据此推算，若采用3×3的核，常规二维卷积运算的乘法运算量是深度可分卷积的九倍。而如果选用5×5的核，常规二维卷积运算的乘法运算量是深度可分卷积的二十五倍。

深度可分卷积存在一些缺点。它减少卷积层中的参数数量。这对小模型来说，如果用深度可分卷积替代二维卷积，模型的性能可能会大幅减弱。因此，最终得到的模型可能是不够理想的。不过，只要使用合理，深度可分卷积可以在不牺牲模型表现的情况下，帮你提升效率。

六、分组卷积

AlexNet 的研究文献，网址为 https://papers.nips.cc/paper/4824-imagenet-classification-with-deep-convolutional-neural-networks.pdf，于2012年首次提出了分组卷积的概念。主要目的是为了使得网络训练能够在两个内存资源紧张的GPU上完成，每个GPU的内存容量为1.5GB。以AlexNet为例，该网络在多数层都设有两条独立的卷积通路。这种方式可以在两个GPU之间分配模型，从而实现并行处理。如果GPU数量进一步增加，还可以采用更多GPU的并行化方案。

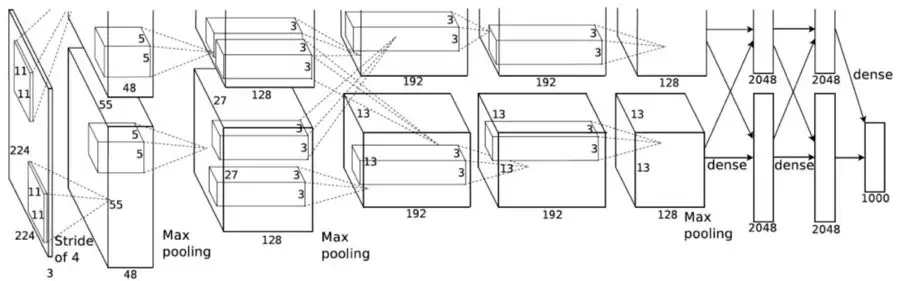
图片来自 AlexNet 论文

这里我们说明分组卷积的运作机制。首先，常规二维卷积的过程如下图所示。在这个情形里，借助128个尺寸为3×3×3的滤波器，将输入层（7×7×3）转变为输出层（5×5×128）。运用而言，就是借助Dout个规格为h x w x Din的滤波器，把输入层面（Hin x Win x Din）进行转换，从而得到输出层面（Houtx Wout x Dout）。

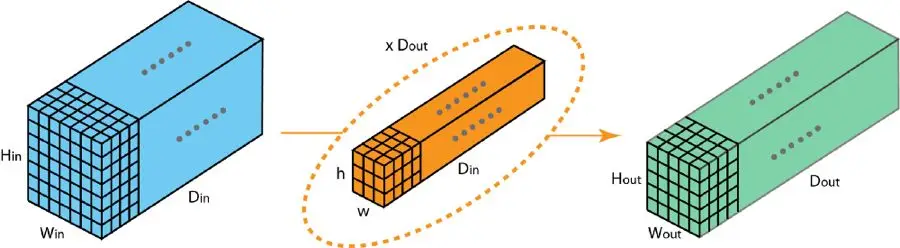
标准的 2D 卷积

在分组卷积操作里，过滤器被划分成多个独立单元，每个单元专门处理特定层级的二维卷积运算，通过这个实例可以更直观地掌握其原理。

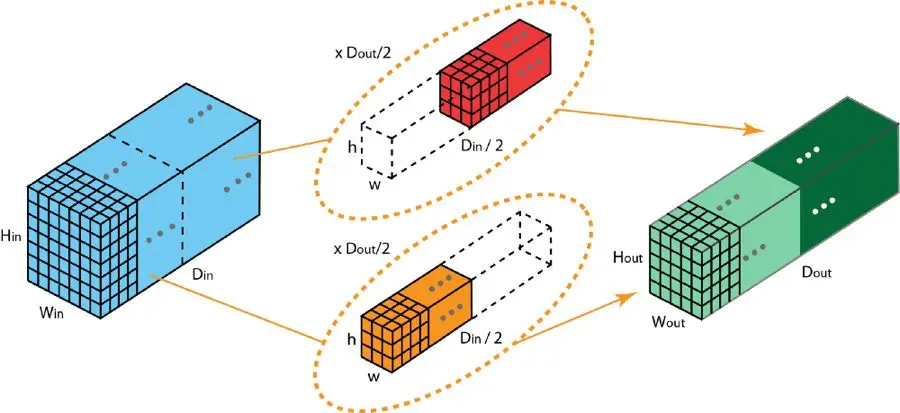
具有两个过滤器分组的分组卷积

图中描绘了采用双组卷积核的分组式卷积结构，每个组内单个卷积核的维度仅为常规二维卷积核维度的一半，具体数值为Din除以二。每组均由Dout除以二个卷积核构成，首个分组（以红色标识）与输入层的前半部分进行交互。

:,:, 0:Din/2

）卷积，而第二个过滤器分组（橙色）与输入层的后一半（

:, :, Din/2:Din

）进行叠加处理。因此，每一个过滤器的集合都会生成Dout/2个通路。从全局角度讲，这两个集合总共会形成2×Dout/2=Dout个通路。接下来，将这些通路并置排列，便构成一个拥有Dout个通路的输出层。

1、分组卷积与深度卷积

你或许会留意到分组卷积和深度可分卷积所用的深度卷积之间有相像之处也有不同之处。倘若过滤器分组的数目和输入层通道的数目一样多，那么每个过滤器的深度就变成了Din除以Din，结果为1。这种过滤器深度和深度卷积中的深度是相同的。

另一方面，当前每个过滤器集合都设有 Dout/Din 个过滤器单元。总体来看，输出层的维度是 Dout。这种情况不同于深度卷积——深度卷积不会导致层维度发生变化。在深度可分卷积的应用中，层维度会借助 1×1 卷积进行后续扩展。

分组卷积有几个优点。

首个好处在于训练过程高效。由于卷积操作被分解为多条路径，每条路径都可以由不同的 GPU 单独执行，因此模型能够以并行方式在多个 GPU 上进行训练。与在单个 GPU 上完成全部任务相比，这种多 GPU 的模型并行化方式能让网络在每个阶段处理更多图像。通常认为模型并行比数据并行效果更佳。将资料集划分为若干组，再逐一训练每一组，这是其中一种方法。然而，若分组数量过多，实际上就变成了随机单步优化，而不是整体批次优化。这种做法会导致处理速度减慢，并且有时会使结果不够理想。

训练极其深层的神经网络时，分组卷积具有相当关键的作用，这在 ResNeXt 架构中得到了印证。

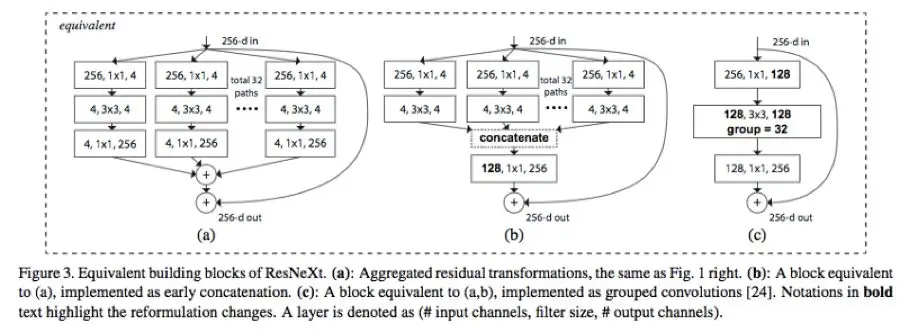
这幅图片源自 ResNeXt 的研究报告，网址是 https://arxiv.org/abs/1611.05431

第二个好处在于模型运行起来更省力，就是说，模型里的数字会随着过滤器集的增多而变少。从前面的情形看，标准的二维卷积有 h x w x Din x Dout 这么多数字。用了两组过滤器的分组卷积，数字变成了 (h xw x Din/2 x Dout/2) x 2 个。数字的总数减了一半。

第三个优点颇为出人意料。分组卷积或许能带来比标准二维卷积更优的模型效果。有篇很不错的博客已经阐述了这一点，链接是：https://blog.yani.io/filter-group-tutorial。下面简单归纳一下相关内容。

缘由与稀疏筛选机制存在关联，具体表现于邻近层级筛选机制间的关联性，此关联性呈现稀疏特征。

在 CIFAR10 上训练的一个 Network-in-Network 模型中，相邻层过滤器之间相关系数的矩阵呈现明显差异，高度相关的过滤器显示为较亮颜色，而相关性较低的过滤器则呈现较暗色调，该图片来源于：https://blog.yani.io/filter-group-tutorial

分组矩阵的相关性映射图又如何？

在 CIFAR10 数据集上训练的 Network-in-Network 架构中，相邻层级间过滤器之间存在关联性，动态图像分别呈现了包含1、2、4、8、16组过滤器的不同情形。相关图片源自 https://blog.yani.io/filter-group-tutorial

图示内容为采用一两个四个八个十六个过滤器实施分组训练后，上下层过滤器间的关联情形，该篇论文阐述了一种推论，即分组训练的成效在于通道方向上获取块对角形态的稀疏分布，网络内部关联度高的过滤器，是借助分组训练以更规整的路径习得的，实际上无需再进行参数化的过滤器关联便不再需要学习大幅降低网络参数规模有助于避免过度拟合现象，这种效果类似于正则化作用，使得优化器能够训练出更为精准且运行效率更高的深度神经网络。

AlexNet conv1 过滤器剖析：依据作者阐述，过滤器划分仿佛会将习得的过滤器构造性地划分成两个不同类别，此图源自AlexNet 论文，

另外，各个过滤器类别都会掌握数据的一个专属模式。正如 AlexNet 的设计者强调的，过滤器类别似乎会将掌握的过滤器在构造上分成两个不同的类别——单色过滤器和多色过滤器。

你认为深度学习领域的卷积还有那些值得注意的地方？

821 次浏览

54