伯努利原理：不仅重要，还如此有趣，绝对脑洞大开！

那个时期的流体力学非常艰深，假如当时有人用这种方式为我们讲解，我确信自己一定能顺利通过考试，现在回想起来，那些经历真是历历在目啊。这篇文章将从案例研究、原理探讨、实践应用三个层面着手，保证让您觉得此番阅读收获颇丰。

天才/学霸/大神——伯努利

伯努利

（Daniel Bernouli,1700～1782）

伯努利是一位瑞士的科学家，他的身份涵盖物理学家、数学家和医学家。他是伯努利家族中最为出色的成员，这个家族在数学领域传承了四代，共产生了十位成员。他在十六岁时便进入巴塞尔大学，开始学习哲学和逻辑学，并成功获得了哲学学衔。紧接着在十七岁到二十岁期间，他转而研究医学，并于1721年取得了医学学衔，之后成为了著名的外科医生，同时担任过解剖学讲师。尽管如此，在父兄的影响下，他最终还是选择了转向数理科学领域。伯努利在诸多领域取得了成就，其中流体力学最为突出，此外还涉及天文观测、重力研究、行星运行轨迹分析、磁现象探讨、海洋学以及潮汐现象研究等。

理论篇——伯努利方程

伯努利方程由瑞士物理学家伯努利创立，为理想流体稳定流动的基础公式，对明确流体内部各点的压力与速度具有重要作用，在水利工程、船舶制造、飞行器领域等被普遍采用。

伯努利方程的推导

在稳定流动的理想流体里，不考虑流体的粘性，每个细小的流管中的液体都符合能量守恒，同时也满足功能原理。

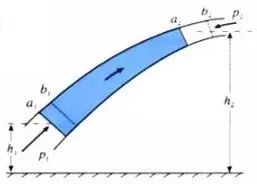
设：流体密度 ρ ，细流管中分析一段流体 a 1a 2：

经过短暂时段 Δt 后，流体 a 1a 2已经运动到了 b 1b 2的位置，从宏观角度分析，这等同于将流体 a 1b 1部分调整到了 a 2b 2区域开元棋官方正版下载，假设 a 1b 1这一段流体的质量为 Δm ，那么：

机械能的增量：

同一流管的任意截面伯努利方程

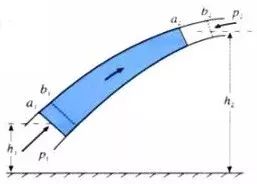
理想流体稳定流动时，同一流管内任一点处，每立方米流体的动能、势能与该点压强之和，是一个固定值

必须留意的是，伯努利方程源自机械能守恒原理，因此它只适用于内摩擦可忽略不计且无法压缩的理想液体。当液体存在内摩擦时，摩擦力会消耗机械能并转化为热量，导致机械能不再守恒，若要将伯努利方程应用于此类情况，需要额外考虑机械能的损耗部分。

应用篇——伯努利方程的广泛使用

丹尼尔·伯努利于1726年阐述了伯努利原理，该原理属于流体力学核心公式。伯努利方程针对理想状态下的稳定流体运动，描述了不可压缩流体在无粘性损耗情况下，沿流线方向任意两点处开元ky888棋牌官网版，压力能量、运动能量与高度能量三者总和恒定不变。这一原理的内在含义是流体机械能守恒，具体表现为动能数值加上重力势能数值再加上压力势能数值，其总和始终维持恒定值。水泵方面表现为：速度水头，加上静水头，再加上位置水头，其总和为固定值。其中特别有名的结论是：在相同的高度下流动时，流动速度快，那么压力就会相对较低。

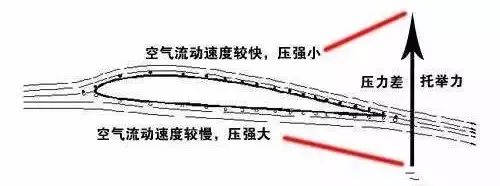
翼型升力

飞机为何能升空，是由于机翼承受了向上的推力。飞机飞行时，机翼附近空气的流动路线分布是这样的，机翼横截面的形状上下不均匀，机翼上方的流动路线紧凑，速度较快；机翼下方的流动路线稀疏，速度较慢。根据伯努利原理可以知道，机翼上方的气压较低，机翼下方的气压较高。因此就形成了施加在机翼上的向上的升力。

离心式水泵

泵体负责收集各叶片甩出的流体，这些流体在泵体内部沿着逐渐增大的蜗形路径行进，速度随之放缓，压力则相应提升，促使流体的运动能（速度势）转变为静定能（静定势），以此降低能量损耗。因此泵体的功能并不仅限于聚集流体，它更是一个实现能量转化的关键部件。

消防炮

消防水泵对水或泡沫液等液体介质进行驱动，使其获得能量后传输至消防炮，而消防炮及炮管的内部通道是逐步变窄的，因此液体运行速度逐步加快，压力逐步降低，使液体的静态压力能（静态高度）转变为动态能量（速度高度）开yunapp体育官网入口下载手机版，从而形成高速水流，最终从消防炮喷出的水流才能实现预期的喷射距离。

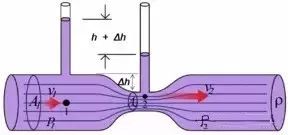
文丘里流量计

文丘里流量计用于检测流体之间的压力差异。这种设备包含一个先变窄再逐渐变宽的管道结构。在变窄部分的直管区域，于两个特定位置测量静压的差别以及对应位置的横截面积，然后借助伯努利原理就能推算出管道中的流体通量。必须留意的是，由于变窄部分产生的能量损耗远小于变宽部分，因此不能使用变宽段的压力数据来计算流量，否则会导致误差明显增大。

虹吸现象

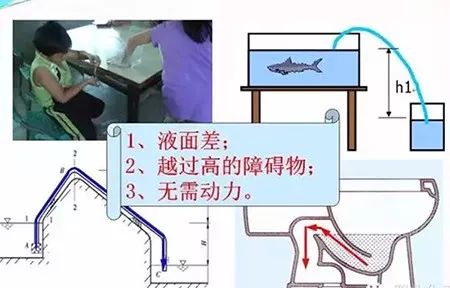
虹吸管

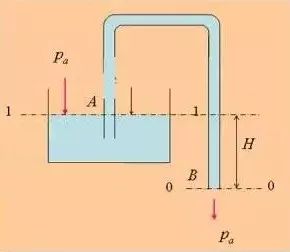
在0-0和1-1面间列伯努利方程：

可得：