pg下载网站麻将胡了 数学思维的妙处（1）：微积分如何指导现实生活？

数学，是很多朋友的噩梦。

有人讲，数数没啥大障碍，学习也没大问题，然而二者合并起来，数学就成了要命的难题。甚至有好多人跨越了数学的关键节点，在大学学习高等数学时仍有想死的感受，情绪激动时甚至要去咒骂牛顿的母亲才能发泄愤怒（微积分是牛顿所发明的）。

可我发觉；好多朋友学不好；甚至心生愤恨；并非数学自身的缘故；而是老师的缘由；他们一开始就做题；持续不停地做题；从不向学生讲述这些数学定理背后的故事；实际上；差不多所有数学概念被发明、被发现；是由于创造者碰到了现实中的问题；想借数学工具去解决问题的 。

比如微积分，牛顿那时为何要发明微积分呢？他究竟是要解决啥问题呢？倘若咱们知晓这背后的缘由，那便理解了微积分的核心，接着从具体回归到数学抽象，去做微积分的题目就会舒坦许多，要是颠倒过来问题可就严重了，原本抽象的就难以领会，而后还要在难以领会的抽象之上拓展更多抽象的推论以及定理。

不糊才怪！

那老师们为何不先从具体的故事出发，又为何不先从具体的问题出发，之后再返回到抽象呢？其原因可能是老师们自己也不清楚微积分究竟是什么，老师们自己也不明白微积分到底是要解决怎样的问题，他的老师们当初也是这般教学的，所以他也如此教我们，另外就是这与老师的绩效并无关联，他们不存在动力去教授这些不考的内容。

以下这些缘由致使一代接着一代的人厌恶数学，并且存在不少人认为，去学习这些令人厌烦的内容，对于我们的现实生活而言有什么作用呢？小学阶段完成加减乘除的学习就行了，能够应对现实生活便足以，还要学习那般的高等数学，那般的微积分，那般的向量，这纯粹是没事找事 。

真的是这样吗？

我觉着并非如此，好多数学当中的思维以及观念，对我们来讲，于现实生活里有着诸多深刻的启迪。

所以，这个名叫《数学思维的妙处》的小系列要介绍几个数学概念，这些概念能给我们的生活、工作、创业带来启发，我保证，一旦你懂得了这四个数学概念，你自身就会发生改变，因为原本混沌的世界在你眼里开始变得清晰了。

当然，首先得交代清楚，我们不停留在解题上，我们致力于偏重思维方式，不到实在没办法，我也不会动用那些使人头大的公式。

我们从很多人最讨厌的「微积分」开始。

（一）牛顿发明微积分，是为了解决什么问题？

瞥见微积分，这般如蚯蚓样子的事物仿若真切地自视线钻入大脑之中，致使好些朋友脑壳生疼。

牛顿为何要发明这么个让后世学子如此头疼的东西呢？

因为他当时遇到了一个问题：

他前面人的理解，在理解速度方面，还非常浅薄，仅仅局限于速度的平均值之上，举例来说，有一个人，花了5分钟的时间，走了100米，那么，这个人的平均速度等于1005，也就是20米每分钟。

但牛顿觉着这太过宽泛，不够细致入微，此人于前行进程里的速度，并非每分钟每秒皆为匀速，我欲知悉其每个瞬间的速度，该如何是好？

那么，我针对这个人的行进过程，实施无限分割，如此一来，难道我不能够获取这个人在每个瞬间所具备的速度吗！

在此情形下牛顿发现了加速度这一概念，存在一个物体处于静止不动的状态，当我们对其施加一次推动时，会在瞬间产生一个加速度，加速度持续累积到一定的程度之后才会产生速度，待速度再次累积到一定的程度以后才会出现位移。

虽说于外视之，乃吾等将物体予以推动之举，然自物体内部观之，整个历程如此：加速度历经累积，进而转变成为速度，彼速度又行累积，最终致使产生位移。

这个过程，就是积分。

翻转过来，便是微分：位移的一阶的导数即为速度，而速度的一阶的导数便是加速度，所以加速度就是位移的二阶的导数。

说白了：

微观累积进而形成宏观，此累积的过程便是积分；宏观进行切分从而得到微观，这切分的过程即为微分。

这仍旧有着一定程度的难以理解，对于这个过程而言，我们去更换一个例子的话，将会显得更加直观，圆的面积是S，它等于πR² 。

凭什么数学家能得出圆的面积公式呀，缘由在于他们施展微积分思维，将圆的面积转变成了长方形面积，：

先把一个圆进行微分，这是第一步，也就是要以其圆心作为中点，将这个圆无限地分割成为扇形，但是我所画的还没有达到无限那种程度 。

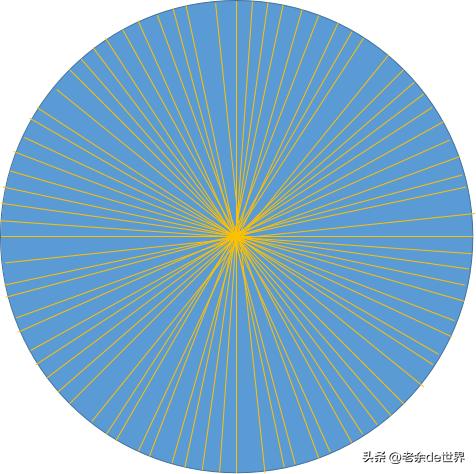
图很丑，您凑合看

第二步：就扇形进行积分，也就是将这些经过无限分割得到的扇形，依次一正一反地做拼接处理，呈现状态如下图所示：

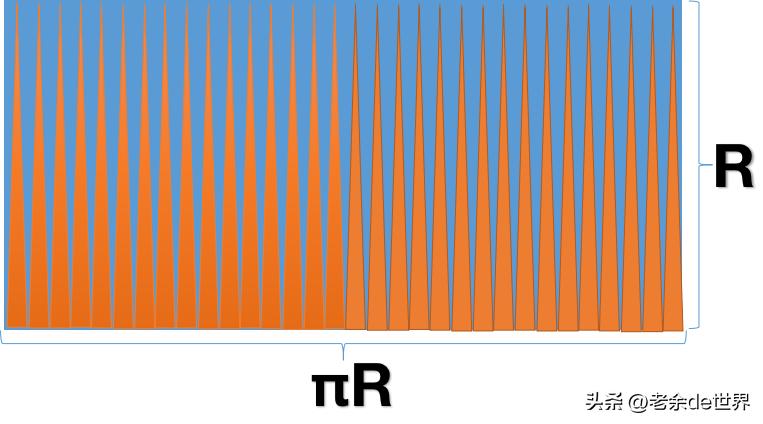
从上面那两个图能够看得出，只要划分得越发细致，圆的面积就会越发接近于这个长方形的面积，只要进行无限的分割，那么这个圆的面积便是这个长方形的面积，而众人都清楚，长方形面积等于长乘宽。

于是圆的面积S=πR（长）️R（宽）=πR×R=πR²。

当下，许多朋友已然无需进行做题了，然而，这般微分、并为之作出恰当积分的进程事宜，究竟能够给予我们日常的生活以何种程度、什么样的启发呢？

其实很深刻。

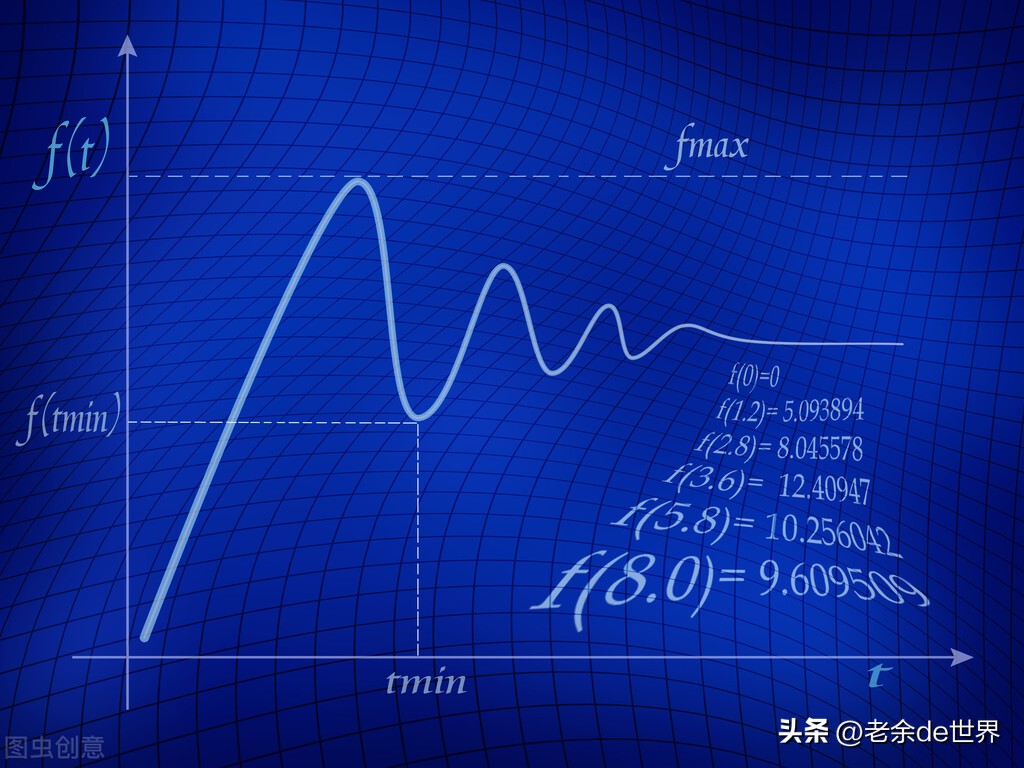
（二）微积分，如何怎么指导我们的现实生活？

我看到了两点：

今日付出努力，此努力不会带来明日成功，不过可为后天成功预备条件 。

在物理世界当中，我们去推某个物体，我们所看到的是该物体在做移动，然而当我们对其施加推力的时候，首先会产生一个加速度，此加速度经过累计过后，才能够产生速度，而这个速度再度累计之后，才可以产生位移。

这与「努力→能力→成功」的过程是一模一样的。

如果你将努力视作加速度，把能力当成速度，把最终的成功看作位移，你瞧瞧是不是这么个过程，那这三者之间的关系实际上就是一个积分的过程。

短暂时间内付出的努力，是无法转变成为能力的，我们必须进行长时间的努力，只有这种如滴水穿石般的努力，才能够积累成为自身所拥有的能力，而从能力积累到取得成功，这同样也是需要花费时间的。

很多人为何一生碌碌无为？

也许并非是欠缺聪慧pg下载麻将胡了安卓专属特惠.安卓应用版本.中国，而是没能领会「微积分的思想」；正所谓无志之人频繁立志，当最初立下做某事的志向时会奋力拼搏一阵pg下载通道，可这一阵的拼搏由于时长过短，并不会随即转化为能力，最终的成功也就无法达成了 。

他的理解或许并非是努力的时长不足pg下载官方认证，而是方向出现了差错，所以他成了那个挖井水的人，他四处挖掘，然而每次快要挖到水的时候就又选择放弃了。

自努力迈向能力的进程中，会将绝大部分人隔开；从能力走向成功，况且也是需耗费时间的，此一过程又会隔绝诸多的人。

在事情最终成功的过程中，会有那么一些人，而这些人在数量方面，少之又少，非常稀少稀缺，而之所以会致使出现这样的情形，是存在着相应的缘由的，当然，运气在其中也是占据着相当重要的地位的。

有志气的人树立长远志向，的确契合了「微积分」思想，从「努力」迈向「能力」，再到「成功」，需要跨越诸多重重关卡，：

持续忍耐，时间之长如同滴水穿石，聚焦之力恰似力出一孔，这些，都是常人难以跨越的，巨大的心理障碍，和行动障碍。

2、今日的懈怠，不会为明日埋下隐患，却会成为后天失败之垫脚石，

众多朋友于生活里，工作中，一贯勤勤勉勉，兢兢业业，不曾有丝毫闪失，然而，于悠悠漫长之路上，却渐渐有所松懈倦怠了。可当懈怠之后，他会满心惊喜地发觉：也并无什么大不了之事啊，我的能力，我的眼光，我的业绩居然俱都未曾遭受什么影响呢。

于是，将懈怠的一堆源于感统协调的说辞找了出来，什么努力并不能对成功起到决定作用，成功靠的更是选择；什么所谓努力只是在付出蛮干的力气，你瞧好些人并未付出努力却也达成了成功等等 。

当断掉那条“努力能导向成功”的想法后，我们的行为就再也寻不回这条路径了，因为“不努力会致使能力下降，进而事情做不成”也是个积累的进程，我们当下松懈了，这种松懈的后果或许要好几个月乃至好几年才会显现。

在这个时候，我们不会自我反省，意识到是几个月的不努力埋下的种子，也不会意识到是几年的不努力埋下的种子。

自我反省却没寻得真正缘由，又怎么能够再次回归到呈现出努力进而生成能力最终收获成功这样一种状态的道路上去呢？

永无可能了！

这可能与人性的弱点有关吧：

在我们奋力拼搏之际，于向他人施以援手之时，内心始终期盼迅速收获回馈；然而在遭遇问题之际，我们一贯寻觅他人方面的成因。

大神-牛顿

（三）结语

微积分发明以前，我们觉得从推力到位移不存在中间进程，我们认为推力乃是位移的直接缘由。

怎会知道，这当中存在着「加速度的累积」，存有「速度的累积」，最终才达成了物体的位移。

同样的道理，世间一切事情都需要经历一个过程，从你起始的点到期望抵达的终点之间，实际上还有好几座山峰需要去翻越，最为可怕的事情是我们处于一种「不知道自己不知道」的状态，当我们对这几座山毫无知晓的时候，就会由于起点到终点的实际情形与你的预期不相符合，进而选择放弃。

这其实就是我们常说的「反馈滞后」。

然而，当我们知晓了「微积分」的思考方式，便会极为明晰这种延迟是实际存在的，：

工作里，我们努力之际，心里会清楚，把努力转化为能力，得有累积，得经历一个过程，从能力累积到成就，同样需一个过程。

身处家庭之中，当我们期望去改变紧张的夫妻关系、亲子关系之际，心里便已明晰自己所做出的改变需有一个过程以供对方接纳，接纳完毕后自己仍要持续前行，这是要促使接受转变为相信，唯有对方相信了，才会对你的改变予以回应，而这一切均需时间。

... ...

第一季《乐队的夏天》当中，九连真人有一首歌，这首歌让我印象深刻，这首歌是《莫欺少年穷》，但是为什么莫欺少年穷呢？

由于少年们当下的积累着实还不算多而言，不过只要在数学里被称作导数的事物够庞大（即积累够迅速），且是在一路前行的过程中，那么在为期不太远的将来，他们所能取得的成就将会无法估量 。

可是要晓得呀，那些年纪轻轻的年少之人，他们所拥有的最为突出的优势之处，竟然是具备了于“求导”整个进程当中能够造就一定成果的关键要素呢。:

——时间。

（完）