pg下载 4.2 伯努利方程
4.2 伯努利方程
按照欧拉运动微分方程的葛罗米柯 - 兰姆形式(二),于各异的限定状况下进行积分,能够得出伯努利积分以及欧拉积分。
4.2.1 伯努利积分
在伯努利积分处于前面那3个限定条件的情形下,进而再增添1个处于沿流线开展积分的这般条件,把式(4.7)里3个式子的两边分别去乘流线上任意一个微元线段dl的3个坐标轴向分量dx、dy、dz,随后再进行相加,于是就有。
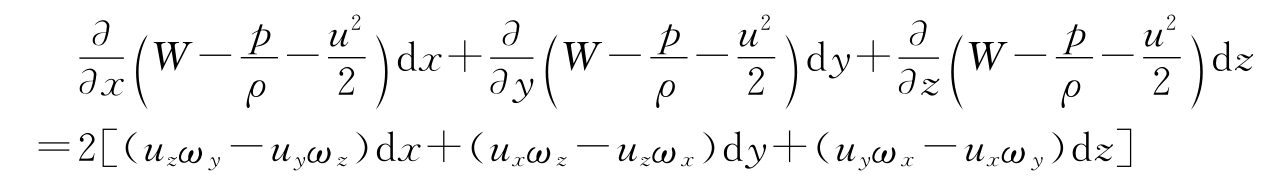
由于是恒定流,各运动要素与时间无关,上式等号左边为
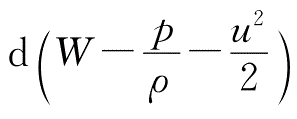
此时,恒定状态下的流,其流线与迹线相重合,呈现出这样的情况:dx等于uxdt,dy等于uydt,dz等于uzdt,基于此番状况,等号右边的数值等于零 。上述式子能够被化简成为。
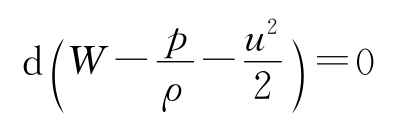
积分后,得

式中:Cl为流线常数,仅适用于同一流线。
4.2.2 欧拉积分
欧拉积分于前面3个限定状况下,再增添1个流动无旋的状况,那么ωx等于ωy等于ωz等于0 。于式 (4.7)里面,等号右侧等同于零,也就是。
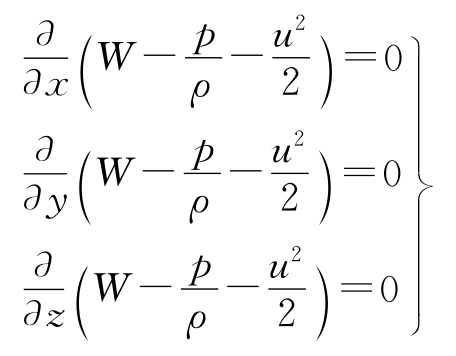
先把上头方程组里的3个式子,分别乘上流场里任意微元线段的dl的3个坐标轴向分量dx,然后乘上dy,接着乘上dz,之后再相加,最后进行积分,就有。

式中:CT称为通用常数,在整个流场中处处适用。
4.2.3 重力作用下的伯努利方程
质量力只有重力时,fx=0,fy=0,fz=-g,有
dW=-gdz
积分得
W=-gz+C
将上式代入式(4.8)、式(4.9),得到伯努利方程:

1. 式(4.10)是在重力作用下,关于理想不可压缩流体恒定流动的伯努利方程。 2. 对于有旋流动,它仅仅沿着流线适用。 3. 而对于无旋流动,它在整个流场中都适用。 4. 元流的过流断面面积是无限小的。 5. 沿流线的伯努利方程同样适用于元流。 6. 所以式(4.10)也被称作理想流体元流伯努利方程。
4.2.4 理想流体元流伯努利方程的意义
于理想流体元流的伯努利方程里头呀:z所代表的是,单位重量流体针对某一个基准面而言,具备的位置势能;这位置势能呢,又被称作位置水头;其单位是m 。
表示单位重量流体具有的压强势能,又称压强水头,单位为m;
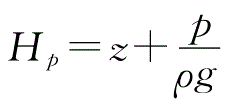
表示单位重量流体具有的总势能,又称测压管水头,单位为 m;
表示单位重量流体具有的动能,又称速度水头,单位为m;
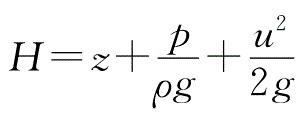
表示单位重量流体具有的机械能,又称总水头,单位为m。
因此,伯努利方程式(4.10)有着这样的物理意义,那就是,当理想不可压缩流体在重力场里作恒定流动时,沿着同一元流(也就是沿同一流线),单位重量流体的位置势能、压强势能以及动能,在流动进程中能够相互转化,不过它们的总和维持不变,也就是说单位重量流体的机械能是守恒的,故而伯努利方程又被称作能量方程。
当理想不可压缩流体于重力场里作恒定流动之际,它沿着同一条一元流(也就是沿着同一条流线),流体的位置水头、压强水头以及速度水头在流动的进程当中能够相互转化,并且各个断面的总水头维持不变哦。伯努利方程式(4.10)的几何意义便是如此这般,也就是总水头线是与基准面相平行的水平线,就如同图4.1所展示的那样。
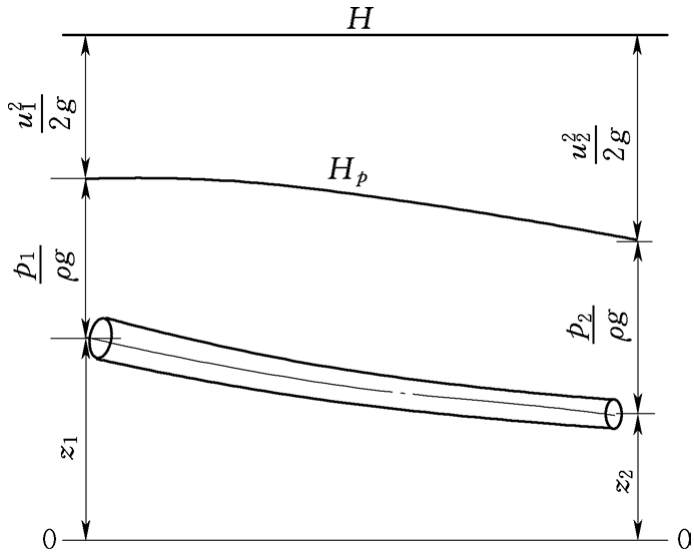
图4.1 理想流体伯努利方程的各种水头
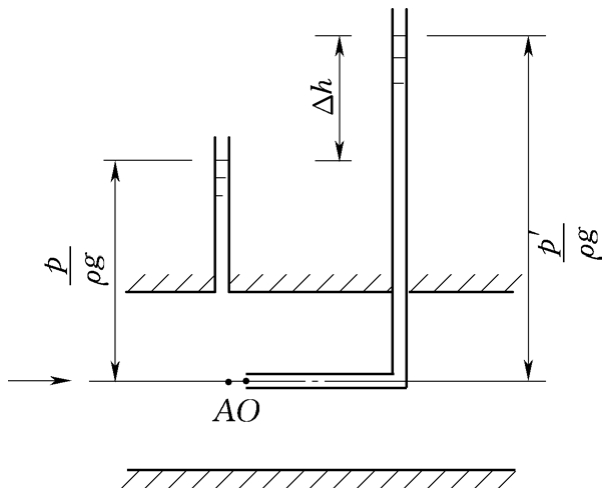
图4.2 点流速测量
4.2.5 理想流体元流伯努利方程的应用
1.毕托管
毕托管,是一种仪器,用于测量点流速,它是理想流体元流伯努利方程在工程里的典型应用 。
想要对流场之内某一个点的速度大小直接去进行测量,这件事确实是比较困难的,然而呢,该点的压强是能够借助测压计轻轻松松地被测量出来的。借助对于点压强的测量,接着使用伯努利方程由此间接地推断出点速度的大小,这便是毕托管的测速原理究竟是什么。就如同图4.2呈现出来的那样,现在打算去测定均匀管流过流断面上A点的流速u,能够在A点所在断面设置专门的测压管,以此测量出该点的压强p,这个压强被称作静压。另外在A点同一流线下游选取相距极其近的O点,在这个点放置一根两端均开口的L型细管,让其中一端管口正好对着来流方向,另一端垂直向上,这样的一根管就被叫做测速管。来流于O点,因受测速管的阻滞,致使速度变为零,其动能全部转化成压能,进而测速管里的液面升高 。
。O点称为驻点,该点的压强称为总压或全压。
将AO所处的流线当作基准,把水头损失予以忽略,针对A点以及O点展开应用理想流体元流伯努利方程的操作:

则A点的流速为

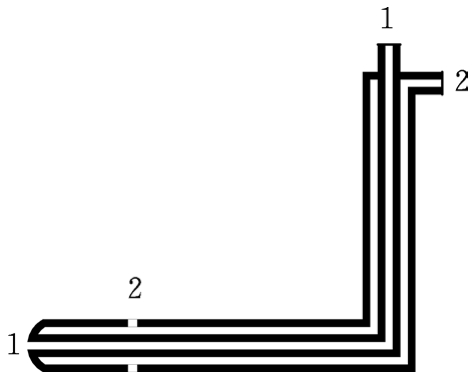
图4.3 毕托管剖面图
把黏性存在这一情况加以考虑,同时将毕托管放进流场后对流动产生干扰等诸多因素的影响也一并顾及,进而引入那个修正系数c,于是。
式中:c为修正系数,数值接近于1,由实验测定。
依据上述原理,把测速管以及测压管组合成用于测量点流速的仪器,此仪器称作毕托管,它的剖面如同图4.3所展示的那样。管1是两端开口的,它作为测速管,其用途是测量总压。管2是侧壁设有几个均匀分布小孔的,它作为测压管,主要用来测量静压。把管1、管2分别连接到压差计的两端,这样就能测得总压与静压的差值了。
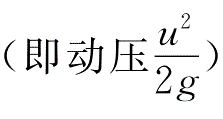
),从而求出测点的流速。
2.相对运动的伯努利方程
离心式水泵里的流体运动属于一种相对运动,图4.4展示的是一离心式水泵的叶轮,叶轮是由叶片以及连接叶片的前、后圆盘构成,后盘安装在原动机转轴上,原动机促使叶轮做旋转运动后,流体从半径为r1的圆周进入到叶轮之中,经由叶片间的流道,从半径为r2的圆周离开叶轮,叶轮以特定的角速度ω进行旋转,流体在叶轮内部,一方面以相对速度w顺着叶轮叶片流动,另一方面以等角速度ω做旋转运动,牵连速度是u=ωr 。
倘若进行假定的话,包括这样两点,一点是流体属于理想流体范畴的情况下并呈现为恒定的流动状态呢;另一点就是叶轮之上的叶片数目达到无穷多这个程度以及叶片不存在厚度这样的情况呢。水流仅仅依照叶片的骨线方向来进行运动,而且相对速度w是与叶片骨线相切着的。
若以v表示流体的绝对速度,则
v=w+u
绝对速度、相对速度以及牵连速度,它们共同构成速度三角形,就如同图4.4显示的那般,在这里面,被称作绝对液流角的α,它是绝对速度和牵连速度之间所形成的夹角,而被叫做相对液流角的β,是相对速度与牵连速度之间的夹角。
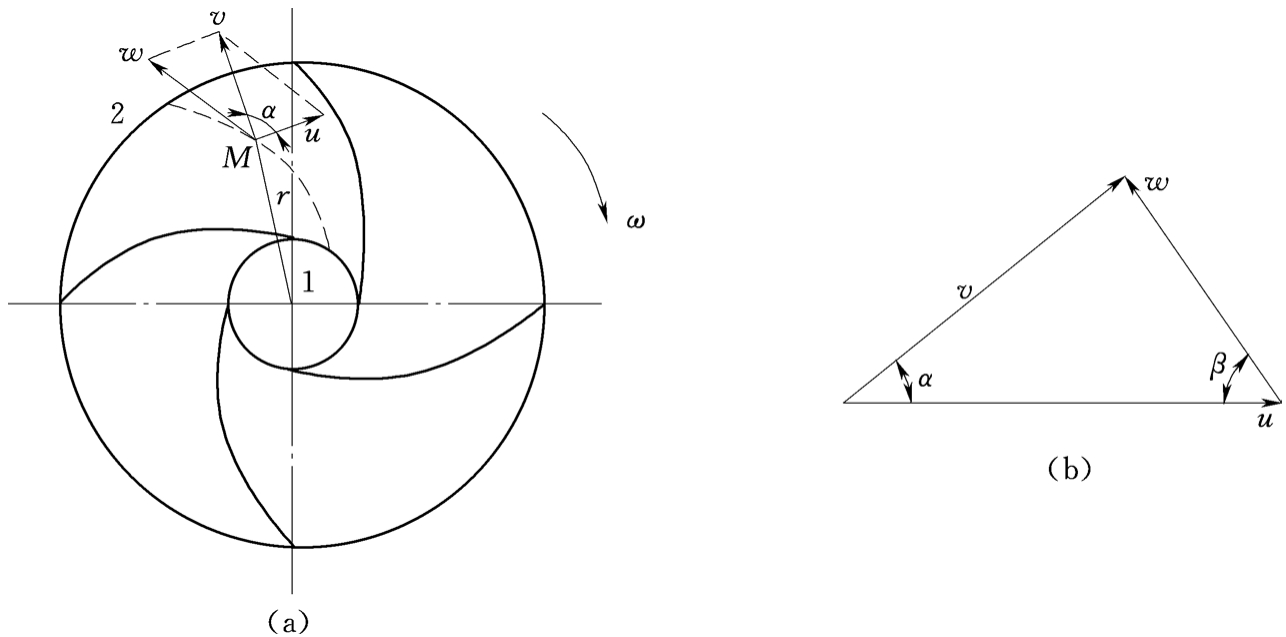
图4.4 相对运动的伯努利方程
(a)叶轮剖面示意图;(b)速度三角形
做一条在流道里的 1 - 2 流线(相对流线),在这条流线上选取一点 M,其欧拉运动微分方程是。

式中:wx、wy、wz为相对速度。
叶轮里面的流体所承受的质量力存在重力以及离心惯性力pg下载,所以,单位质量力的表达式子是。
fx=ω2x,fy=ω2y,fz=-g
将式(4.13)中各式分别乘以dx、dy、dz,再相加,有
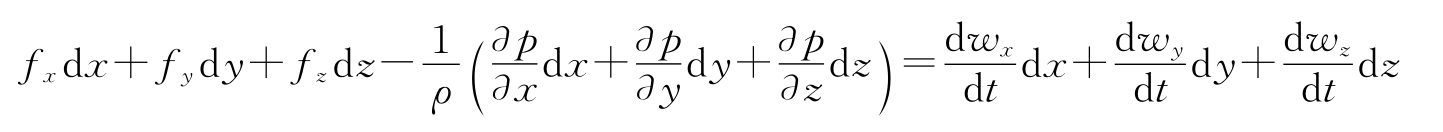
代入单位质量力的表达式,得
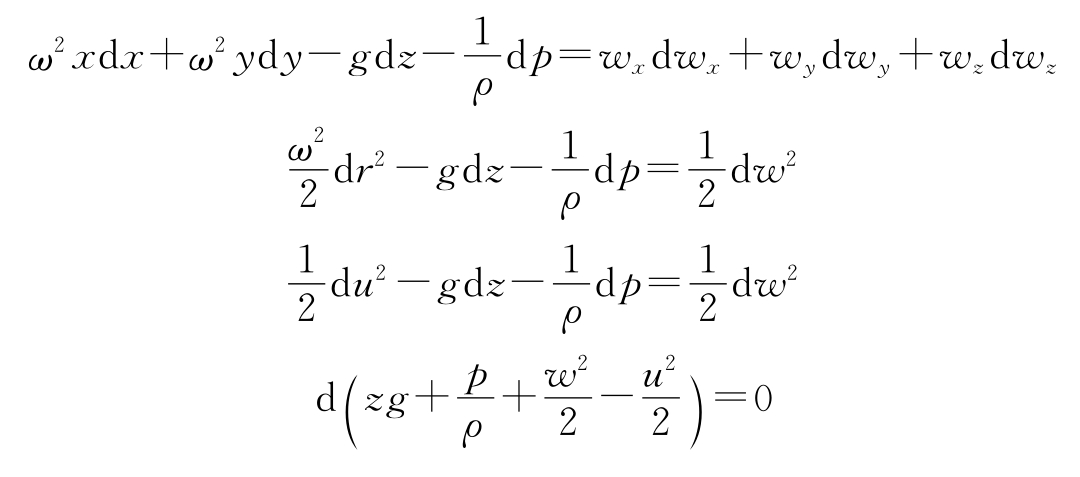
积分后,得
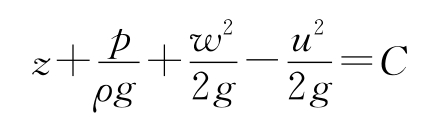
对流线上任意两点1、2,有
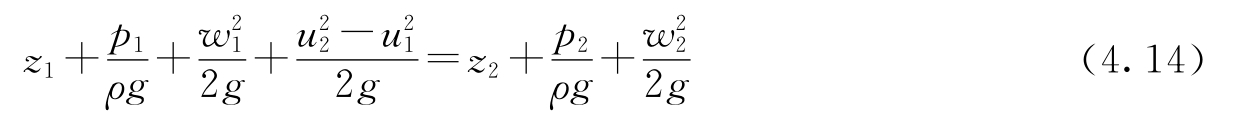
式中:
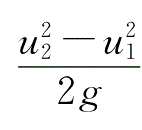
为单位离心力对流体所做的功。
式(4.14)是不可压缩均质理想流体恒定流相对运动的伯努利方程,它常被用于分析流体机械,像离心式水泵、风机以及水轮机里的流体运动。
4.2.6 黏性流体元流的伯努利方程
按照能量守恒原理,能够把伯努利方程从理想流体延伸到黏性流体,黏性流体于流动进程中会生成流动阻力,去克服阻力做功,流体的一部分机械能会不可逆地转变为热能耗散掉,所以,流体的机械能顺着流程减小,总水头线顺着流程下降,在运动进程里,单位重量流体的位能、压能、动能以及损失的能量总和,应当等于运动起始时的位能、压能、动能总和,也就是 。
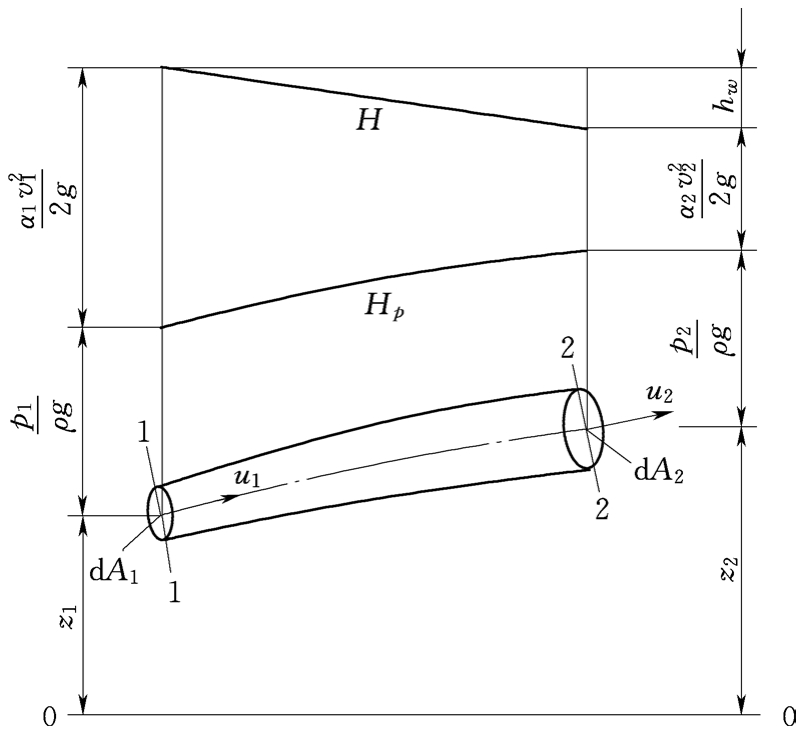
图4.5 总流伯努利方程
其中,h′w是单位重量黏性流体沿着流线从1点流动至2点时的机械能损失,它被称作元流的水头损失,单位是m 。
上式称为黏性流体元流的伯努利方程。
4.2.7 黏性流体总流的伯努利方程
实际工程里,管道内的流动是有限断面的总流,渠道内的流动也是有限断面的总流,所以有必要把黏性流体元流的伯努利方程推广到总流。
当呈现出如图4.5那样的情况时,这是黏性流体恒定总流,其中过流断面1 - 1属于渐变流断面,其面积是A1,过流断面2 - 2同样是渐变流断面,面积为A2。在该总流里任意选取元流,此元流的过流断面存在微元面积,分别是dA1、dA2,其位置高度分别是z1、z2,涉及的压强为p1、p2,流速为u1、u2。
将黏性流体元流伯努利方程式(4.15),两边同时乘以重量流量,重量流量为ρgdQ,而ρgdQ又等于ρgu1dA1,且等于ρgu2dA2,由此得到单位时间通过元流两过流断面的能量方程,得单位时间通过元流两过流断面的能量方程:

对上式积分,可得单位时间通过总流两过流断面的能量方程:

下面分别确定上式中3种类型的积分
(1)
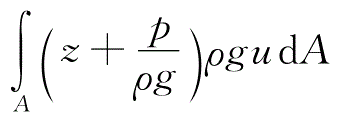
。因所取过流断面11、22为渐变流断面,面上各点
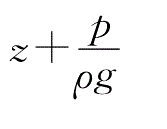
=C,于是
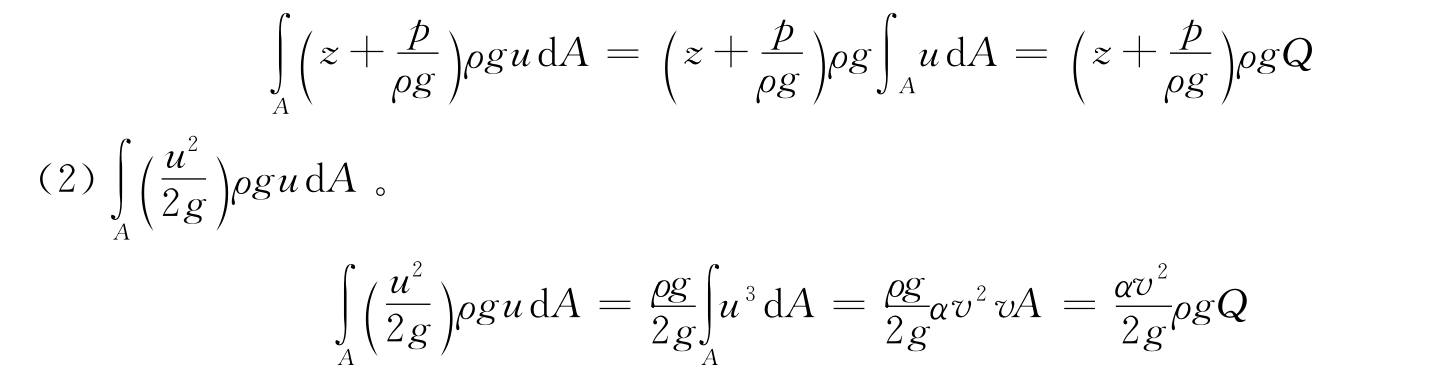
式中:α为动能修正系数。
修正用断面平均流速代替实际流速计算动能时引起的误差。即
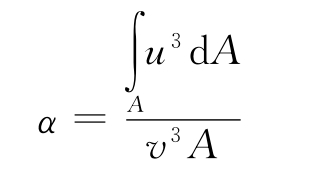
α值由过流断面上速度的分布情形所决定,当流速分布相对均匀之时,α取值为1.05至1.10,当流速分布并非均匀之际,α值会比较大,一般选取α为1.0 。
(3)
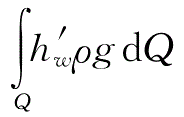
。单位时间总流从过流断面11流到22的机械能损失
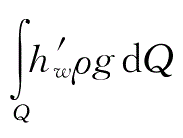
不易通过积分确定,可令
在式子当中,hw所代表的是,单位重量的流体,从过流断面1 - 1流动到2 - 2时,所产生的平均机械能损失,而这个平均机械能损失,被称作是总流的水头损失。
将以上积分结果代入式(4.16),得
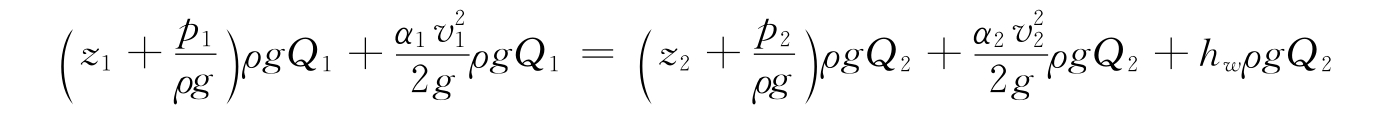
因为两个断面之间不存在分流以及汇流的情况,所以得出ρgQ=ρgQ1=ρgQ2,进而使得上面的式子被简化成为。
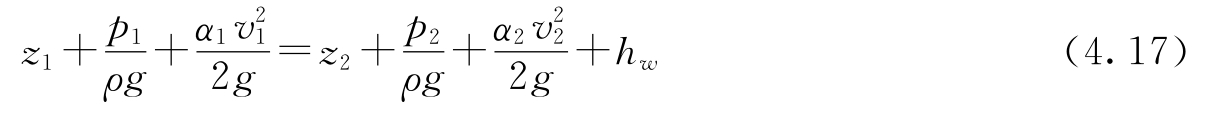
对于实际流体总流而言,式(4.17)是其对应的伯努利方程。要是式当中的hw等于0,那么。
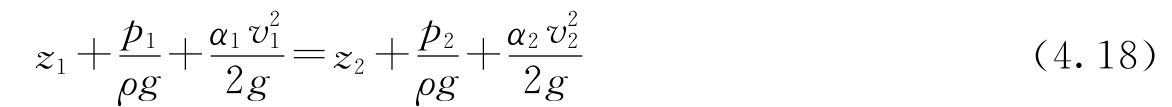
式(4.18)为理想流体总流的伯努利方程。
各项在总流伯努利方程式里的意义,跟元流伯努利方程中的对应项相类似,不过,要注意总流伯努利方程里各项具备“平均”之义,比如:
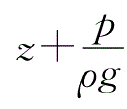
于总流过流断面之中,针对单位重量的流体而言,所具备的平均势能,鉴于渐变流过流断面之上, 。
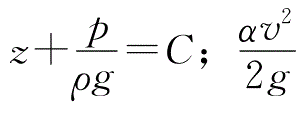
为,存在于总流过流断面上,针对单位重量流体而言,所具备的平均动能;hw为,处于总流两个过流断面之间,针对单位重量流体来说,其平均机械能损失 。
应用总流伯努利方程时必须满足下列条件:
(1)恒定流动。
(2)质量力只有重力。
(3)不可压缩流体。
所取的过流断面,属于渐变流断层或者均匀流断面的范畴,然而,在两个过流断面之间,是准许出现急变流情况的。
(5)两过流断面间无分流或汇流。
(6)两过流断面间无其他机械能输入输出。
应用总流伯努利方程时还需注意以下几点:
过流断面,得做选择呢,不仅须把那渐变流的断面或者均匀流的断面给选出来,而且一般情况下,要在那些包含了较多已知量的断面里边选,或者得在含有需求要知晓的未知量的断面里面去进行 picking up啦。
(2)过流断面上用于计算的点,原则上能够随意去选取,之所以如此,是由于在均匀流或者渐变流的断面之上,任意一点的测压管水头都是相等的,也就是。
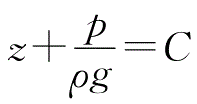
,并且过流断面上的平均速度水头
并非关联于计算点的位置情况,然而要是计算点挑选得适宜恰当,那么能够让计算极大地简化,举例来说,管流的计算点平常选择在管轴线上边,明渠的计算点一般选择在自由液面上头。
(3)基准面是被任意选取出来的水平面,不过通常要让z处于正值状态。同一方程必然得凭借同一基准面去进行度量,不同的方程能够采用不一样的基准面。
(4)方程里的压强 p1和 p2,可以用绝对压强,也能用相对压强,然而同一方程,必须采用同一种压强来进行度量。
4.2.8 水头线及水力坡度
总水头线是沿程各断面总水头
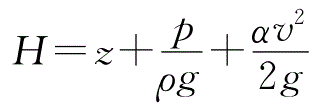
进行连线。参照图4.5来看,理想流体的总水头线呈现为水平线,而黏性流体的总水头线在沿程过程中却是单调下降的,下降的快慢是通过水力坡度J来表示的:

因dH恒为负值,在
前加 “-”号,确保J为正值。
测压管水头线是沿程各断面测压管水头
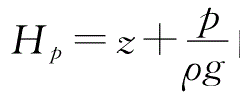
与的连线。因为测压管水头的大小受到速度水头的影响,所以测压管水头线在沿着路程的时候情况多样,可以上升,能够下降,也会保持水平模样,它变化的缓急程度是用测压管水头线坡度Jp来表示的:
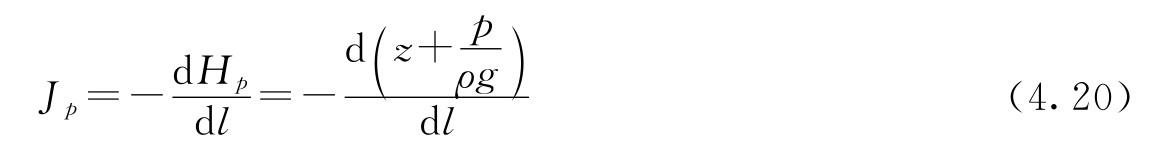
当测压管水头线下降时,Jp为正值,反之,为负值。
4.2.9 总流伯努利方程的应用
1.文丘里管
一种用于测量管道流量的仪器是文丘里管,它是总流伯努利方程在工程里的典型应用实例。文丘里管由三部分构成,分别是收缩段、喉管以及扩散段。在文丘里管收缩段的进口处和喉管那儿安装测压管或者压差计,以此测出两断面的测压管水头差,然后依据伯努利方程就能够实现对流体流量的测量了。
如图4.6所示,选定水平基准面0-0,将收缩段进口断面设为1-1,把喉管断面设为2-2,1-1断面与2-2断面均属于渐变流断面pg下载渠道,各计算点选取在管轴线上,其中1-1断面的平均速度、压强、过流断面面积分别是v1、p1、A1 ,2-2断面的平均速度、压强、过流断面面积分别为v2、p2、A2 ,流体密度是ρ ,列出1-1、2-2断面的伯努利方程, :
图4.6 文丘里流量计
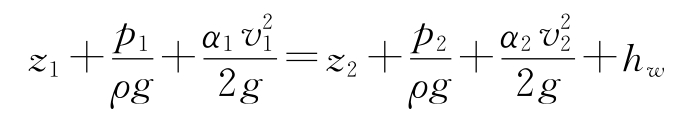
因为收缩段的水头损失极小,所以能够让hw等于0 ,选取动能修正系数α 1等于α 2等于1.0 ,于是上式被简化为 。

列1-1、2-2断面连续性方程:
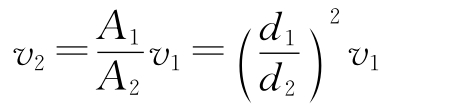
代入前式,得
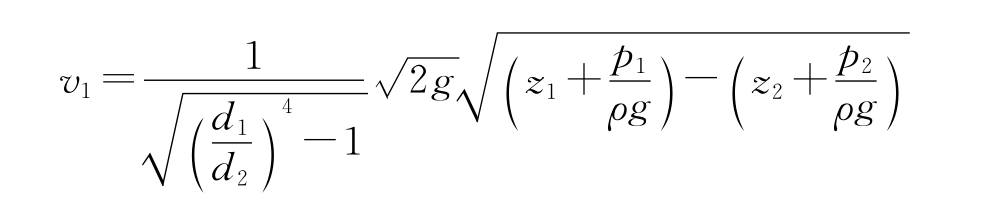
则通过文丘里管的流量:
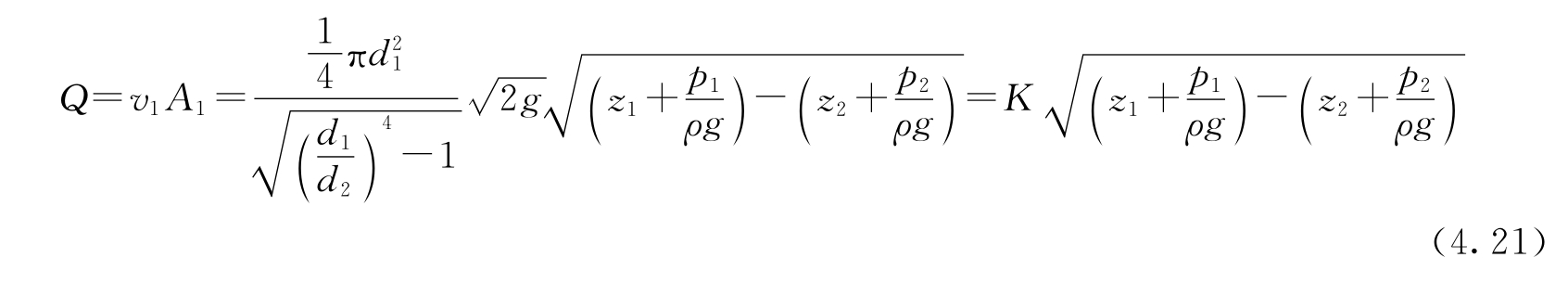
式中:

为由文丘里管结构尺寸d1、d2而定的常数,称为仪器常数。
装测压管时,测压管水头差:
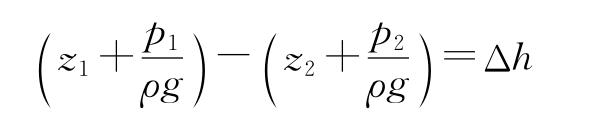
装压差计时,测压管水头差:
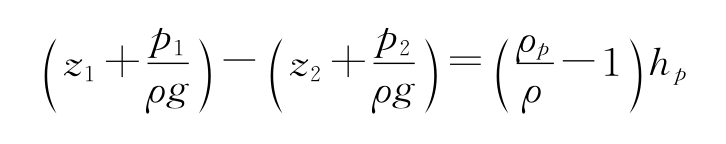
将值代入式(4.21),鉴于两断面间实际存在能量损失,引入流量系数ψ,如此便可得。
装测压管时:
装压差计时:
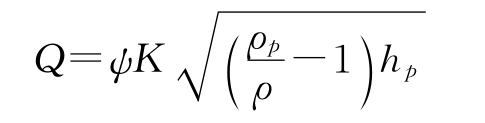
2.沿程有能量输入或输出的伯努利方程
总流伯努利方程式(4.17),是在两过流断面间不存在其他机械能输入输出的条件下导出的,虽然当两断面间安装有水泵、风机或者水轮机等流体机械装置时pg下载赏金下载,流体流经水泵或者风机会获得能量,流经水轮机将失去能量,但若设单位重量流体获得或失去的能量为Hm,依据能量守恒原理,还是可得有能量输入或输出的总流伯努利方程:
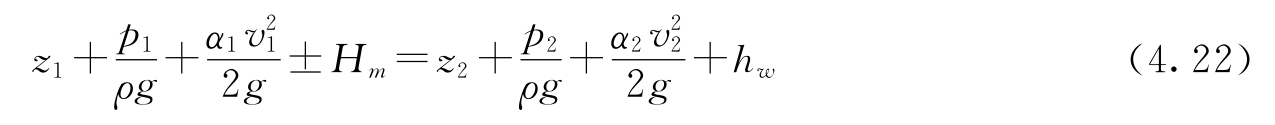
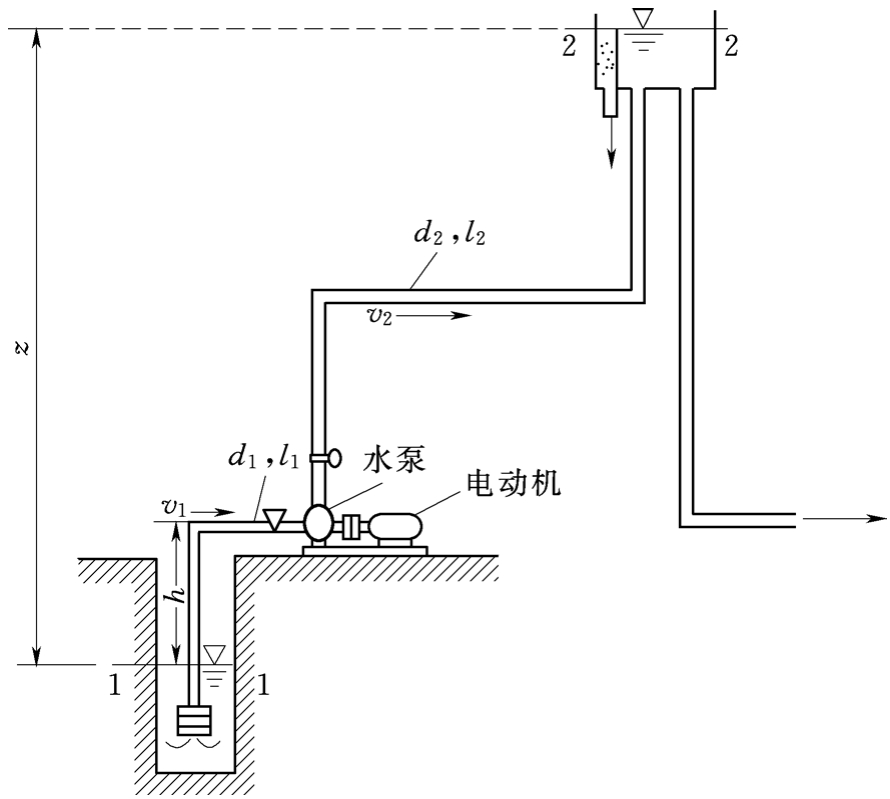
图4.7 安装有水泵的管路系统
这里面,在式子当中,H m之前的那个“±”记号,意味着,要是所得到的能量,那就是“+”,而要是所失去的能量,那便是“-” 。
在如图4.7所示的管路当中,存在着一个水泵,该水泵针对水流进行做功,以此让水流的能量得以增加,随后列出1 - 1断面以及2 - 2断面的伯努利方程。
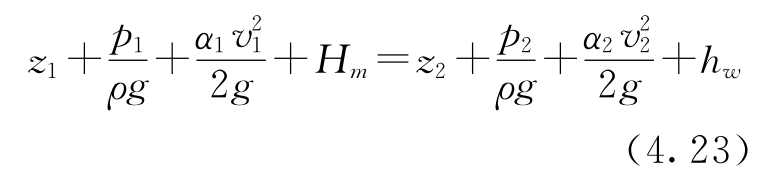
只因p1等于p2还等于pa,v1、v2针对管内流速而言是很小的,那就能够认为v1等于v2且等于0,如此一来上式便被简化为。
式中:z为上、下游水面高差,也称为提水高度或扬水高度。
单位时间当中,原动机给予水泵的功被称作水泵的轴功率P , 有单位时间里,通过水泵的水流重量是ρgQ , 进而单位时间里水流从泵中实际获得的能量为ρgQHm ,它被称为水泵的有效功率Pe , 鉴于水泵内存在诸如漏损、水头损失、机械摩擦损失等各类损失 , 于是有效功率Pe小于轴功率P ,就算Pe 。




