如何通俗易懂地解释卷积？

卷积这个术语，早先就接触过，却始终未能理解透彻。书本里常会陈述它的含义，列举诸多特性，又借助案例和图像加以说明，然而究竟为何要这样构建，这样运算，其深层道理却大多含糊其辞。一个物理学者的体会是，公式若不能提供贴合现实的形象化说明，便感觉有所缺失，认为并未真正领会其精髓。

教科书上一般定义函数 的卷积 如下：

连续形式：

离散形式：

此外也说明了，先将g函数进行反转，等同于在数轴上把g函数从右侧折向左侧，这就是卷积中“卷”字含义的出处。

接着把g函数位移至n，在此处计算两个函数相应位置的乘积，随后将所有乘积加总，这就是卷积运算中“累加”的环节。

这种方式仅从运算角度阐释了公式，算术层面确实没有问题，然而深入探究，为何要先将对象颠倒再进行位移，这样安排的缘由仍然让人难以理解。

许多热心网友运用卷地毯、丢骰子、打耳光、存钱等生动比喻阐释卷积概念，这些例子读来颇具趣味性，然而深入探究，仍觉部分内容阐释不够透彻，或许存在不足之处，亦或许尚有提升空间，后续将对此进行剖析。

苦思冥想了两个夜晚，总算对一些困惑有了些领悟，因此提笔与网友交流，一起进步。

明确一下，这篇文章主要想解释两个问题：

卷积这个术语如何进行阐释？“卷”具体指代什么含义？“积”又代表什么意义？

2. 卷积背后的意义是什么，该如何解释？

考虑的应用场景

为了更好地理解这些问题，我们先给出两个典型的应用场景：

1. 信号分析

一个输入信号f(t)输入到线性系统开yun体育官网入口登录app，该系统的特性由单位冲击响应函数g(t)表征，那么其产生的输出信号是什么？实际上，采用卷积运算能够求得该输出信号。

2. 图像处理

输入一张图像f(x,y)，通过专门设计的卷积核g(x,y)实施卷积运算，输出图像会呈现出模糊化，边缘突出等不同效果。

对卷积的理解

卷积这个概念可以这样认识，两个函数的卷积，首先需要把其中一个函数进行颠倒处理，接着让这个颠倒后的函数在另一个函数上移动，并计算它们重合部分的叠加结果。

连续情形里，叠加表示计算两个函数相乘后的积分，离散情形下则是进行加权求和，为了方便起见，将这两种方法都称作叠加。

整体看来是这么个过程：

颠倒，接着是移动，然后是合并，再来是移动，接着是合并，再来是移动，然后是合并，如此循环。

多次滑动得到的一系列叠加值，构成了卷积函数。

卷积中的“卷”表示函数的镜像变换，即将 g(t) 转化为 g(-t) 的操作；此外，“卷”还蕴含着移动的概念，这一点借鉴了网友李文清的见解。倘若将卷积称作“褶积”，那么“褶”字仅能体现翻转的内涵。

卷积的“积”，指的是积分/加权求和。

部分论述只关注层叠运算的累加过程，却忽视了函数的逆向操作，这种观点存在缺失；另一些文献对“卷积”概念的阐释，实质上是指代“积分”，属于概念混淆。

对卷积的意义的理解：

从积累的过程能够看出，我们获得的累加量，是一个整体性的认识。以信号处理为例，卷积的成效，不仅取决于当前时刻输入信号的反馈值，还取决于先前所有时刻输入信号的反馈，顾及了以往所有输入所产生的效果的汇集。图像处理里，卷积处理的效果，就是把每个像素点邻近的，乃至整个图像的像素点都纳入考量，对当前像素点实施某种加权运算。所以说，“积”体现的是全局性，或者说是一种“融合”，将两个函数在时间维度或空间维度上进行交织。

为什么要搞“卷”？直接相乘不可以吗？我认为，“卷”（翻转）其实是为了施加一种限制，它明确了在计算“积”时应该以什么为基准。在信号处理的情境下，它规定了在哪个特定时刻的邻近区域进行“积”，在空间处理的情境下，它规定了在哪个具体地点的附近进行累加运算。

举例说明

下面举几个例子说明为什么要翻转，以及叠加求和的意义。

例1：信号分析

输入信号为 f(t)，其值随时间波动。系统响应函数为 g(t)，如图所示该函数随时间呈指数形式递减。这一特性表明：若在 t=0 时刻施加输入开yun体育app入口登录，则该输入会随时间逐渐减弱。具体而言，当时间达到 t=T 时，原先在 t=0 时刻的输入 f(0) 将会减小至 f(0)g(T)。

由于信号是持续不断地传送的，也就是说，每个瞬间都有新的信号传输进来，因此，最终的输出结果实际上是所有先前输入信号叠加在一起的整体表现。根据下图所示，在时间点T等于10的时候，输出值与图中被特别指出的部分密切相关。那个f十的值，由于是刚刚输入的，因此它的计算结果应当是f十乘以g零，而时间点九的输入f九，仅仅经历了一个时间段的减弱，因此它引发的回应应当是f九乘以g一，依次类推，也就是图中虚线所显示的规律。这些点逐一相乘，再进行累计，便得出T等于十时的输出数值，这个数值同样代表函数f与函数g在T等于十时的叠加效果。

那个关系式样子不太美观，是颠倒的，因此，我们让g函数进行镜像处理，变为g(-t)，这样就显得顺眼了，注意到了吗？这就是卷积需要“卷”起来，并且要反转的缘由，这是从它的实际意义中推导出来的。

图中虽然已经调整方向，但位置仍显不妥，因此需要再移动T个单位，形成下图所示效果。这个图形能够直观展示卷积运算的原理，与我们文章开头所描述的定义完全吻合。

因此，针对T时刻的卷积运算，需要坚持的规则是：t加上T减去t等于T。这个规则的作用，读者可以自行领悟。

例2：丢骰子

在名为如何通俗易懂地解释卷积的问题中，位列首位的马同学提供了一个极为精彩的比喻，他借助掷骰子的过程来阐释卷积的实际用途，相关插图选自该同学的著作，特此致谢

需要计算的几率是：存在两个骰子，将它们同时掷出，两个骰子显示的数字总和等于4的可能性有多大？

考察一下开元棋官方正版下载，两颗色子数值合计为四的组合有三种情形：第一颗是1，第二颗是3，总和等于四，第二种是两颗色子都是两，总和等于四，第三种是第一颗是3，第二颗是1，总和等于四。

因此，两枚骰子点数加起来为4的概率为：

写成卷积的方式就是：

在这里我想进一步用上面的翻转滑动叠加的逻辑进行解释。

首先，两个骰子的点数总和为4，要符合这一要求，我们仍然需要对函数 g 进行反转处理，接着将阴影部分上下对应的数值相乘，最后将所有乘积结果加总，这其实就是在计算当自变量等于4时的卷积结果，具体示意图请参考下图。

此外，经过这种转换，能够便捷地延伸以计算两个骰子点数总和为 n 的几率，这就是函数 f 与 g 的卷积 f*g(n)，如图所示：

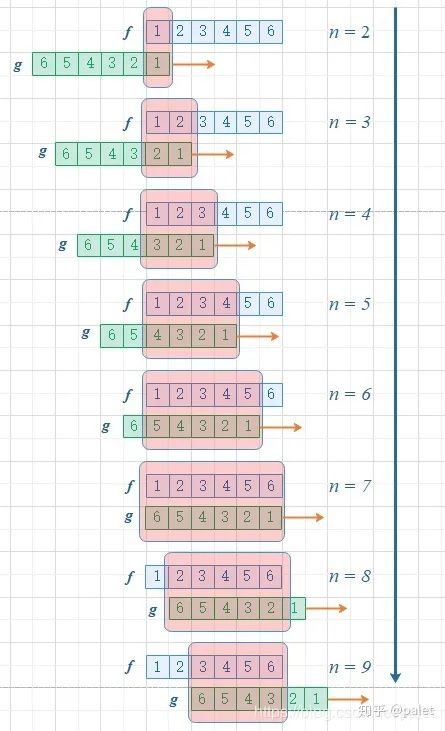
从图中可以观察到，函数 g 的变化，导致点数和增加。这个案例中，对 f 和 g 的限制因素就是点数和，同时它也是卷积函数的输入值。若想进一步探究，可以尝试计算，当两个骰子每个面出现的几率相同，点数和为 n=7 时，出现的可能性最高。

例3：图像处理

图像可以表示为矩阵形式（下图摘自马同学的文章）：

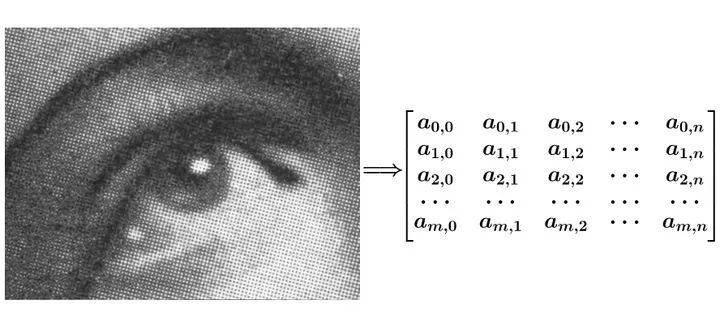
图像的平滑操作或边缘检测功能，同样能够通过一个g矩阵来体现，例如：

注意，我们在处理平面空间的问题，已经是二维函数了，相当于：

那么函数f和g的在（u，v）处的卷积 该如何计算呢？

按卷积的定义，二维离散形式的卷积公式应该是：

卷积的界定方式涉及两个维度，即x轴和y轴，这对应于离散公式中的下标i和j，理论上这两个维度都应延伸至无限大，从负无穷延伸至正无穷。然而，现实应用中，这些维度总是受到限制。以图像处理中的函数g为例，它实际上是一个3x3的矩阵，表明除了中心位置之外，其它所有位置上的值都为零。鉴于这个情况，原先的公式实际上已经简化了，它仅仅选取了坐标（u,v）周边的点来进行运算。因此，实际的操作流程是：

首先我们在原始图像矩阵中取出（u,v）处的矩阵：

接下来将图像处理矩阵进行反转，这个反转方式存在多种解释，但实际作用相同：或者先沿着横轴颠倒，再沿着纵轴颠倒，或者先沿着纵轴颠倒，再沿着横轴颠倒，具体操作如下：

原始矩阵：

翻转后的矩阵：

（1）先沿x轴翻转，再沿y轴翻转

（2）先沿y轴翻转，再沿x轴翻转

计算卷积时：

这个公式有个显著特征，参与乘法的变量a和b的下标相加总是等于（u,v），这是为了对加权求和施加限制。这也是需要翻转矩阵g的理由。之所以这样设置矩阵下标并实施翻转，是为了让大家更直观地理解其与卷积的联系。这样做有利于后续的推广，也有助于揭示其物理层面的含义。计算过程中，通常采用颠倒之后的矩阵，直接进行矩阵内积运算即可。

此处所算为（u,v）点的卷积值，沿着横轴或纵轴移动，能够得出图像所有点的卷积值，其得到的结果便是经过多项变换后的图像，包括平滑化以及边缘检测等操作。

仔细琢磨一下，在计算图像卷积时，我们直接选取了原始图像矩阵中 u,v 位置的数据，之所以选择这个位置的数据，根本原因在于要符合之前所说的条件。需要计算点（u，v）的卷积，g矩阵为3x3结构，其下标必须与（u,v）相加满足条件，因此只能选取原始图像中围绕（u，v）点的3x3区域，也就是图中被标记的部分的矩阵。

换个角度来看，假如g矩阵的规模不是3x3，而是变成了7x7，那么我们便需要在原始图像选取以（u，v）为基准点的7x7矩阵来实施运算。从这里可以看出，这种卷积运算实际上是将原始图像里邻近的像素点全部纳入考量，进而达成混合效果。邻近的范围大小由g矩阵的维数决定，维数越高，牵涉到的周边像素点就越多。矩阵的构造方式，决定了混合生成的图像与原始图像相比，是会变得不清晰，还是更加清晰。

例如，该图像处理矩阵通过整合邻近像素的数值进行计算，导致画面细节减弱，整体呈现朦胧感，使图像更加柔和，轮廓变得模糊不清。

这种图像处理矩阵能够突出像素值差异显著的区域，增强轮廓线，对于数值变动较小的部分则不受干扰，从而实现轮廓提取的目标：

参考资料

关于慧维智能

慧维智能医疗科技有限公司是2019年6月建立的机构，主要业务包括智能医疗产品的开发、制造以及市场推广。公司的主要人员，都具备在国内外知名研究单位和高知名度企业的工作背景。慧维智能凭借人工智能和边缘计算方面的自主创新技术作为支撑，着力向全球医疗行业供应品质卓越、价格合理且使用感受出色的医疗器械和配套服务，从而显著增强医疗专业人士的诊疗成效与作业速率。