斐波那契数列有什么生活应用吗？

一、斐波那契的生活应用：

斐波那契数列中的数值在现实生活中时有体现，比如松果的鳞片分布、凤梨表皮的纹路、树叶的叶序排列、某些植物花朵的瓣数（以向日葵为例）、蜂巢的构造、蜻蜓的翅膀形态、数学常数e的推算、黄金几何图形、黄金比例概念、等角螺旋形态、音乐中的十二平均律等。

斐波那契数也能在植物的部分部位观察到，比如叶子和枝条。举例来说，从树木的枝干上选定一片叶子，将其编号为0，接着按顺序数数开yun体育app入口登录，数到与它正对着的叶子为止，那么这些叶子之间的数量通常就是斐波那契数。叶子从一个位置移动到下一个正对位置的过程，可以看作是一个循环。

二、矩形面积的价值体现在很多方面，比如：

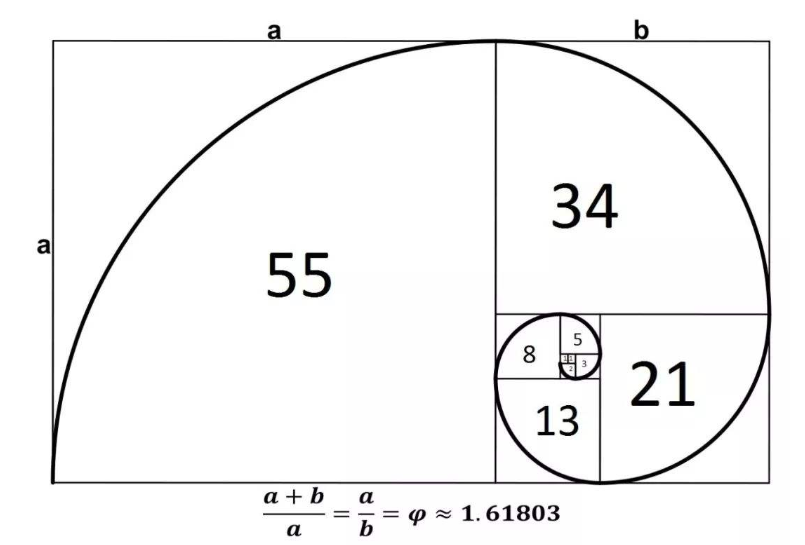
斐波那契数列同矩形面积的形成存在关联，据此能够引申出该数列的一项特性。该数列初期各项的平方值，可视作尺寸各异的正方形。依据斐波那契的递推关系，这些正方形能够组合成一个整体矩形，因而所有小正方形的面积总和恰好等于大矩形的面积。

三、在科学领域没有被广泛应用。

扩展资料

1、“斐波那契数列”的定义：

这个序列由数字 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368等项组成。从第三位数字起开元棋官方正版下载，该序列的任意一项数值都等于它前面两个数值的总和。

2、“斐波那契数列”的发现者：

发现斐波那契数列的人是那位意大利数学家列昂纳多·斐波那契，他生活在1170年到1250年之间，来自比萨开yunapp体育官网入口下载手机版，人们常称他为“比萨的列昂纳多”。

1202年，他创作了《算盘全书》。他是欧洲首位探究印度与阿拉伯数学学说的学者。他的父亲受比萨某商业组织之托出任外交代表，任职于阿尔及利亚，列昂纳多便得以跟随阿拉伯导师钻研数学。他还曾在埃及、叙利亚、希腊、西西里及普罗旺斯等地学习数学。