pg下载赏金下载 伯努利方程与现实生活的奇妙联系与应用

一、伯努利方程的命名由来

存在于流体力学诸多理论里，伯努利原理有着极为关键的地位，它详尽说明了流体里速度跟压力间的相互关联，也就是动能与压强势能间的相互转换，然而伯努利方程，恰恰是这一原理的数学化呈现，此一重要理论是由一位卓越的瑞士科学家丹尼尔·伯努利于1726年提出来的，历经两百多年的发展以及验证，直至如今依旧被看作是经典。

二、伯努利方程的具体形式

于流体力学范畴之内，连续介质理论方程之构建仍有待时日，然而伯努利原理却已然变成水力学领域之中的基本原理了。其关键要点在于流体的机械能守恒。伯努利方程的具体呈现形式如下：

在式子当中，p所代表的是流体里特定一点的压强，那v是该点的流速， ρ是流体的密度，g是重力加速度，而z是该点所处的高度。为了能够更加具体地去理解伯努利方程，我们可以挑选流体中的A、B两点来开展探讨，伯努利方程同样是适用的，并且能够表述为：

是以能量守恒观念去闸释，伯努利方程能够被理解成：于流体里头pg下载渠道，动能、重力势能以及压力势能的总和维持不变。据此，我们能够推导出一项关键结论：在相同的高度状况下，流速要是越快，压力就越小；要是流速较为缓慢，压力就相对而言较大。这样一种现象，通常被称呼为伯努利效应。

三、伯努利方程的适用范围

伴随着所有的原理，伯努利方程同样有着它专门的应用范畴，它的运用遭受以下这些限制条件的管束，这些条件分别是：

流体得是那种没有粘性的，流体是不可以被压缩的，流动得是那种稳定持久，也就是说流动相关参数不会随着时间改变的。流动得是顺着同一条路径开展的，也就是沿着线路而流动的。

需要留意的是，要是考量能量损耗，伯努利方程同样能够应用于粘性流体。然而在日常的生活当中，我们所碰到的流体一般都是带有粘性的，除非是处于特殊状况下的超流体。要是对这个感兴趣，能够自己去查找有关超流体的资料。

四、伯努利方程在生活中的应用

伯努利方程pg下载网站麻将胡了，这算得上是经典理论，在生活里头有着广泛的应用。流体，这里说包括气体以及液体，当它流速增快的时候，其压强会相应减小，而流速减慢的时候，压强就会增大。这一原理能够解释很多，我们日常生活当中碰上的场景。下面是一些常见的例子，当你再次碰到这些情景的时候，不妨运用伯努利效应来解释看看，彰显一下你的学识。

4.1、地铁或高铁等候时的安全距离

当地铁或者高铁以很快的速度驶过来的时候，其十分强大的气流带动方面的效应，致使人与车辆二者之间的空气流动速度迅速剧增，依据伯努利方程，流动速度的增加会致使压强降低，所以，人与地铁或者高铁之间产生了明显显著的压强差，形成了一股非常强大的推力，要是站在黄线以内的范围，这股推力有可能会把人朝着车辆推过去，造成并非必要的伤害，故而，为了安全的缘故，我们应当始终时刻保持在黄线外边的安全距离。

4.2、飞机升空之谜

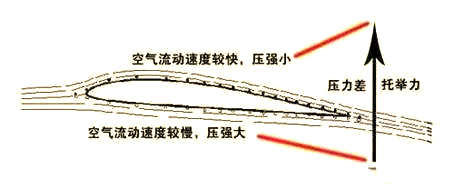
飞机机翼设计匠心独具，其横截面形状上下并非对称，致使机翼周围空气流线分布存在差异。具体而言，机翼上方流线更为密集，流速相对较大，下方流线较为稀疏，流速较小。这种差异致使机翼上方压强低于下方，进而产生向上的升力。另外，负压涡流为飞机升力增添一份力量。正是这些升力共同发挥作用，让飞机得以翱翔蓝天。

4.3、汽油发动机的化油器

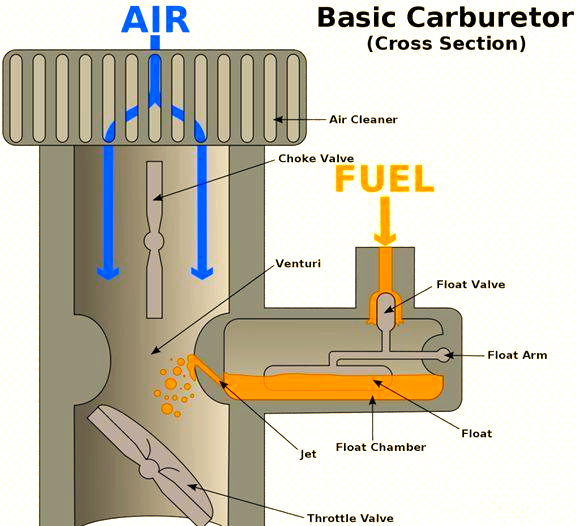
在汽缸的活塞开展吸气冲程之际，空气会被吸进化油器的管道当中，化油器是向汽缸内提供燃料与空气混合物的关键装置，当空气流经管道狭窄部分之后，因流速提升而压强下降，这就致使汽油从喷嘴那儿喷出，并且被雾化成细微的油滴，这些油滴与空气相混合，形成油气混合物，跟着进入汽缸，为发动机供给所需的燃料，其工作原理相当精妙。

4.4、帆船逆风航行的奥秘

帆船在逆风的状况下能够迅猛地向前航行，而这背后的原理跟机翼的升力形成机制是颇为相像的。和硬邦邦的平面不一样，帆船的帆面在受到风的时候展现出了一种三维空间的形态。这种独特的弧形设计致使沿帆下风面的气流同沿帆上风面的气流之间产生了压强的差异，进而给帆船提供了向前的推力。当帆船船头与海风的方向维持大约30 - 40度的夹角的时候，这种推动的效率会达到最佳的状态。在2000年8月，有一艘名为“Hydroptere”号的帆船，它是由法国人精心设计的，在风速仅仅只有15节的情形之下，它居然能够以35节的速度快速行驶，这个速度约合70公里时速，这充分展现了帆船逆风航行时的卓越性能。值得一提的是。

4.5、球类中的弧形球

有种足球技术名为弧旋球，或者常被叫做“弧线球”pg下载麻将胡了，又或者被称作“香蕉球”，它在足球运动里可重要啦。运动员用特定脚法去踢足球时，足球就会在空中沿着一条呈弧线的轨迹向前飞行。就拿右脚球员来说，当他们用右脚内侧“搓”球时，足球就会得到逆时针方向的旋转。这种旋转跟球面摩擦产生的气流相互起作用，进而形成一个和球旋转方向相同的气流环。因为球左侧的空气流动速度比较快，然而右侧相对较慢，这样就在球周围产生了一个属于横向的压力差，也就是马格努斯力。正是这种力量，致使原本朝着右边飞行的“香蕉球”，渐渐朝着左边产生偏转。相反的情况是，运用左脚内侧搓起来的“香蕉球”，先是朝着左边飞行，而后又朝着右边偏转。如此一来，达成了弧形球那种独特的飞行轨迹。

于实际生活之中，伯努利原理或者方程的应用场景多得数不过来，此处没办法逐个详细叙述。不过，经由上述那几个示例，相信您能够由此及彼，领会到伯努利原理或者方程在流体力学里被称作经典的深厚魅力。