pg下载渠道 详细解读高斯滤波---卷积和积分运算

信号处理里，有个关键性的运算是卷积。开始学习卷积之际，常常处于连续的状况下。

关于两个函数，也就是f(x)以及g(x)，它们之间的卷积，则是∫f(u)g(x - u)du。

的确，证实卷积的某些特性并非难事，像是做交换操作，以及结合操作等等，然而对于卷积运算的源头，刚开始学习的人就不太清楚了。

其实，从离散的情形看卷积，或许更加清楚，

对于两个序列f,g,一般可以将其卷积定义为s= ∑fg

卷积的一个典型例子,其实就是初中就学过的多项式相乘的运算,

比如(x*x+3*x+2)(2*x+5)

一般计算顺序是这样,

(x*x+3*x+2)(2*x+5)

然后合并同类项的系数,

2 x*x*x

3*2+1*5 x*x

2*2+3*5 x

2*5

----------

2*x*x*x+11*x*x+19*x+10

事实上，依据线性代数能够晓得，多项式形成一个向量空间，它的基底能够选择为。

{1,x,x*x,x*x*x,...}

如此,则任何多项式均可与无穷维空间中的一个坐标向量相对应,

如,(x*x+3*x+2)对应于

(1 3 2),

(2*x+5)对应于

(2,5).

线性空间里头，并未对两个向量之间定义卷积运算，有的仅仅只是加法、数乘这两种运算，然而实际上，多项式的乘法行为，是没法依托线性空间做出诠释的，由此能够看出，线性空间的理论局限性达到何种程度了。

但如果按照我们上面对向量卷积的定义来处理坐标向量,

(1 3 2)*(2 5)

则有

2 3 1

_ _ 2 5

--------

2 3 1

_ 2 5

-----

6+5=11

2 3 1

2 5

-----

4+15 =19

_ 2 3 1

2 5

-------

10

或者说,

(1 3 2)*(2 5)=(2 11 19 10)

回到多项式的表示上来,

似乎很神奇,结果跟我们用传统办法得到的是完全一样的.

换句话,多项式相乘,相当于系数向量的卷积.

其实,琢磨一下,道理也很简单,

卷积运算事实上是单独去求x乘以x乘以x的系数，x乘以x的系数，x的系数，1的系数，这意味着，它把加法以及求和混合在一起进行操作了。（传统的方式是先开展乘法运算，而后在合并同类项之际才实施加法运算）

若以x乘以x的系数作为例子，会得出x乘x的结果，或者是让x乘x去乘以5，又或者是用3乘以x去乘以2乘以x，即如此。

2 3 1

_ 2 5

-----

6+5=11

实际上，确实是向量内积。这样一来，卷积运算这般情况呢，可以当作是一串内积的运算。既然它是一串内积运算，那么我们就能够尝试用矩阵去表现上述过程。

2 3 1 0 0 0

0 2 3 1 0 0

==A

0 0 2 3 1 0

0 0 0 2 3 1

0 0 2 5 0 0

' == x

b= Ax=

2 11 19 10

'

采用行的观点看Ax,则b的每行都是一个内积。

A的每一行都是序列的一个移动位置。

---------

显然，在这个特定背景当中，我们清楚，卷积具备交换、结合等定律，原因在于，众人皆知的是，多项式的乘法拥有交换律、结合律，在一般情形之下，实际上也是成立的。

处于此地，我们察觉到多项式，除了构建成特定的线性空间之外，基与基相互之间还存有某种特殊的关系，恰恰是这种关系，给多项式空间赋予了特殊的性质。

在学习向量之际，通常会列举这个事例，甲拥有三个苹果，五个橘子，乙具备五个苹果，三个橘子，那么总共拥有几个苹果、橘子呢。老师再三叮嘱，橘子便是橘子，苹果就是苹果，绝对不可以混淆在一起。所以存在(3,5)+(5,3)=(8,8)。没错，橘子与苹果不管怎样相加，都是不会出现任何问题的，然而，要是思索橘子乘橘子，或者橘子乘苹果，这个问题就不太容易阐释清楚了。

又比如说复数，要是只是把复数定义成为数对（a，b），只是在线性空间这个层面上去看待C2，那可就太简单啦，事实上，只要再加上一条（a，b）*（c，d）=（ac - bd，ad + bc）。

则情况马上改观，复变函数的内容多么丰富多彩，是众所周知的。

另外，回想一下信号处理里的一条基本定理，频率域的乘积，等同于相对应的时域或者空域信号的卷积，正好跟在此处的情形完全对等，这后面究竟存在着什么样的隐态联系，需要持续深入地参详。

基于这里的视角而言，高等的卷积运算实际上不过是一种被抽象出来的初等运算罢了。在中学所学的数学范畴之内，实际上还蕴藏着许多高深的内容（诸如交换代数之类）。温习过往从而获取新的认知啊，这话的确没错呢。

实际上这道理并非一丁点复杂，历经多少万年时间人类持续地繁衍着，然而在过去跨度可观的诸多岁月里，不少人们仅仅晓得男性与女性的交合，才方可达成繁衍滋生后代的成效。可精子，以及卵子被发觉，还有生殖机制展开研究，是只是较近这些年份内所出现的事情。

据说孔子讲过道是存在于人们日常的人伦关系当中的，如此一来好像我们理应运用更多带有审视性质的眼光去看待周边的一切，一直到自身，如此这般才能够知晓其呈现出来的样子，进而明白它这样的缘故。

依据上文我们知晓了卷积的源头，我们再去寻觅卷积的官方定义，即为数学里针对两个函数的一种无穷积分运算，对于函数 f1(t)以及 f2(t)，其卷积呈现为其中：“*”是卷积运算符号。

在泛函进行之时的分析里头，这个卷积也就是旋积亦或者摺积，其英文是Convolution，它于应用上是依靠两个函数f以及g从而生成第三个函数所用数学层面算子，通过表徵去呈现函数f 经过翻转，还有平移过后与g的重叠部分的累积情况。函数f与g所形成的卷积，记录下来是f(t)*g(t)，它是其中一个函数翻转还要加上平移之后与另一个函数的乘积的积分，并且是一个针对平移量的函数。

函数f跟g的卷积能够被定义成这样没错没错：z(t)等于f(t)跟g(t)做卷积，z(t)等于f(t)乘以g(t)，z(t)又等于对f(m)乘以g(t-m)进行积分dm。

并且，卷积定理表明，存在二个二维连续函数，有关其在空间域里的卷积，能够通过求其相应的二个傅立叶变换乘积的反变换而获得。相反地，在频域中的卷积，可借助其在空间域中乘积的傅立叶变换而得到。

着实，讲了这般许多，我依旧不是特别清楚为啥要针对图像开展卷积，如何去实施卷积。

1.2 卷积运算

提起卷积运算，首先必然绕不开的便是卷积核，这个卷积核，实际上就是一个大小恒定、由数值参数所构成的数组，数组的参考点一般处在数组的中心位置，数组的相应大小被称作核支撑。单从技术层面来讲，核支撑实际上仅仅是由核数组的非零部分组合形成的。又或者，如同其他的表述方式，卷积核就是人们所说的模板。

卷积运算，可被看作是加权求和的过程，图像区域中使用到的每个像素，会分别与卷积核（权矩阵）的每个元素对应相乘，所有乘积的总和，被当作区域中心像素的新值。

卷积示例：

3 * 3 的像素区域R与卷积核G的卷积运算：

R5（中心像素）等于，R1G1 加上，R2G2 加上，R3G3 加上，R4G4 加上，R5G5 加上，R6G6 加上，R7G7 加上，R8G8 加上，R9G9。

要是针对一幅图像开展卷积运算，能够借助以数组为中心当作参考点的3*3卷积核。首先把核的参考点确定在图像的首个像素点处，核的其余元素覆盖图像总共其对应的局部像素点。对于每一个核点，我们能够获取这个点的值以及图像里对应图像点的值。把这些值相乘然后求和，并且将这个结果放置在与输入图像参考点所对应的位置上。通过在整个图像上扫描卷积核，对图像的每个点重复进行此操作。最终能够得到图像的卷积图像。

确实，能够借助方程去展示这个进程，并确定图像以I(x,y)来明晰，核以G（i,y）予以命名(此中数字0)，参照的点处于（ai,aj）相关坐标之上，那么卷积H(x,y)便如此定义：

H(x,y) = sum

I(x+i-ai,y+j-aj)G(i,j)

.常用模板（卷积核）

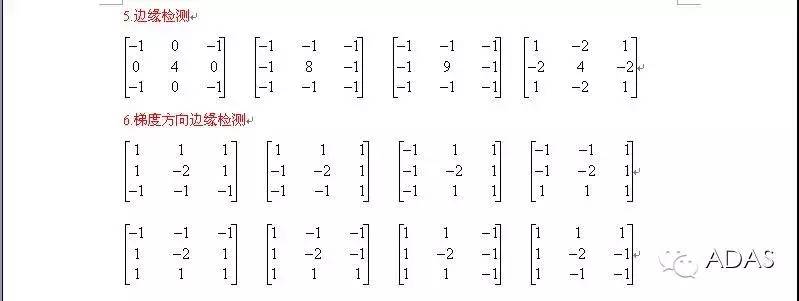
连续空间的卷积有着这样的定义，那就是，f(x)与g(x)进行卷积的结果，是f(t - x)g(x)在t从负无穷一直到正无穷这个区间上的积分值。需要注意的是，t - x必须要处于f(x)的定义域范围之内，如此一来，看上去范围极大的这个积分，实际上最终的取值范围还是在一定的区间范围之内的。

实际的过程是，f(x)，先进行Y轴的反转，接着沿X轴平移t，得到f(t - x)，之后拿来g(x)，将二者乘积的值进行积分。想象一下，若g(x)或者f(x)是单位的阶越函数，那便是f(t - x)与g(x)相交部分的面积，这就是卷积了。

把积分符号换成求和就是离散空间的卷积定义了.

1.3 意义

各种图像变换的基础是卷积，卷积核（模板）的形式决定一个特殊卷积所实现的功能，用高斯函数对图像进行卷积就是高斯变换。

平滑处理有平滑多种类型，其中包括简单模糊，即对邻域求和再缩放，还有简单无缩放变换的模糊，也就是单纯对邻域求和pg下载麻将胡了，而中值模糊是进行中值滤波，高斯模糊是采用高斯卷积，双边模糊又是应用双线性滤波。

膨胀和腐蚀。

图像金字塔

拉普拉斯变换、canny算子（求导数）

卷积性质：

一个式子，它用符号表示卷积，表明卷积属于特殊类型的乘法，乘法的某些代数性质能够用于卷积。

结合律：f1(t)与f2(t)相乘的结果等于f2(t)与f1(t)相乘的所得结果，其中这种运算规律被称作交换律。

(2)distributive law：f1(t)*

f2(t)+f3(t)

=f1(t)*f2(t)+f1(t)*f3(t)

(3)associative law：

f1(t)*f2(t)

*f3(t)=f1(t)*

f2(t)*f3(t)

(4)移位不变性：要是有f1(t)乘以f2(t)等于f3(t)，那么f1(t减去t0)乘以f2(t)，会等于f1(t)乘以f2(t减去t0)，且都等于f3(t减去t0)。

此性质说明，不管是哪一个函数发生了平移，平移的距离是t0。然后呢，这样得到的卷积pg下载官方认证，就是仅仅进行了相同距离的平移，而且其大小以及形状都维持不变。

3.奇异信号的卷积特性：

(2)δ(t)*δ(t)=δ(t)

(3)f(t)*δ'(t)=f'(t)

(4)

推行：f(t)乘δ(k函数即delta-函数)(t)等于f(k函数即k阶导数函数)(t) ，f(t)乘δ(k)(t减t0)等于f(k)(t减t0)。

（5）f(t)与δ'(t)和u(t)相乘pg下载麻将胡了安卓专属特惠.安卓应用版本.中国，等于f'(t)与u(t) 相乘，结果为f(t) ，f(t)与δ''(t)和tu(t)相乘，等于f''(t)与tu(t)相乘，结果是f(t)。

2 积分图像

在surf算法里，会用到积分图像的概念，借此将图像与高斯二阶微分模板的滤波变成对积分图像的加减运算，积分图像也就是Integral Image的概念是由viola和Jones提出来的，把类似积分图像用于盒子滤波是由Simard等人提出的，哎，这一堆的概念真是让人头大啊！

积分图像里，任意的一点（i，j）具有的值，对于此的值为ii，而(i,j)，它是跟原图像左上角到任意这一点（i,j）相应的对角线区域，其灰度值的总和，也就是这样。

于公式里头，I(x`,y`)所体现的是原图像之中点（i`,j`）的灰度数值，而ii（x,y）能够借由下述的两公式凭借迭代的方式来予以计算得出：

在公式里头，S（x,y）这一符号所代表的乃是一列的积分情况，并且S（i,-1）的值确定为0，ii(-1,j)的值也确定为0。若要求得积分图像，只是需要针对原图像的全部像素进行一回完整扫描就行。如下所展示的代码乃是针对c++语言的相应实现。

pOutImage = pInImage;

将pInImage加上pInImage，得到的结果赋给pOutImage。

for(int y=1; y< nHeight ;y++)

int nSum = 0;

for(int x=0; x < nWidth;x++)

nSum = pInImage;

pOutImage= pInImage+nSum;

如图所示，在求取窗口w以内的像元灰度总和时，无论窗口W的大小究竟怎样，都能够借助积分图像的4个相应点，即（i1,j1）、（i2,j2）、（i3,j3）、（i4,j4）的值计算得出。也就是说，求取窗口W以内的像元灰度总和，跟窗口的尺寸并无关联。窗口W以内的像元的灰度总和为。

下面看以截图，相信都可以看懂

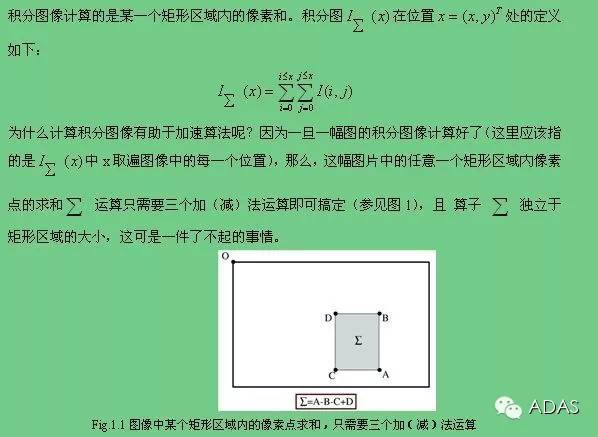
矩形区域以内像素点的相关求和，应当属于一种简单重复性的运算，运用这种思路，总体而言提升了效率。为何会这样讲呢？假定一幅图片一共有n个像素点，那么计算n个位置的积分图，总共的加法运算存在n - 1次（郑重提醒：并非）。

天哪，得充分运用递推思想呀），把各个结果存于一个跟原图相对应的矩阵M里头。要是需要算图像当中某个矩形区域里所有像素的总和时，就如同查表那般，调出A、B、C、D四点的积分图值，通过简单的加减法（留意只需三次哦）便能求得结果。反过来讲，要是用naive的办法直接在原图像的某个矩形区域里求和，你琢磨琢磨，总共可能的矩形组合有多少？ 且对于一幅图像n而言那可非常大，所以2^n！不过，先别急着下定论。可以做个小对比试验，找两组不同的图像，一组用当前方法，另一组用naive方法。在相同环境下运行，看看具体的时间差异。也可以多找些人，分别用这两种办法计算不同图像，收集大家的反馈。说不定会发现，实际情况比想象的更复杂。也许在某些特定图像场景下，现有方法优势明显；但在另一些场景，naive方法也有它的闪光点。所以，各种角度考量后做决定才更靠谱。

那可是天文数字，并且这里面绝大多数的矩形存在重叠，重叠究竟意味着什么呢？在进行求和计算时会有重复性的工作，实际上我们能够有效地运用已经计算过的信息。这便是积分图法的内在思想，它事实上是先计算 n 个互不重叠（专业来讲是不相交）的矩形区域内的像素点总计求和，充分借助这些数值（已有数值）来计算未知值，有点类似递进推导的意味，这就彻底规避了重复求和运算。

这样就可以进行2种运算：

在图 2.3 中如所示，任意一矩形区域之内像素的积分情况，可以借助图像那经过积分得到的图像，便利很快捷地计算出在画面里任意矩形当中所有像素的灰度积分，举例来说，点 1 的积分图像 ii1 的值是（这里 Sum 代表求和）：

ii1=Sum（A）

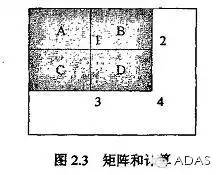
同理，点2、点3、点4的积分图像分别为：

ii2等于把A求和再加上把B求和，ii3等于把A求和再加上把C求和，ii4等于把A求和加上把B求和加上把C求和加上把D求和。

在矩形区域D当中，全体像素的灰度积分是能够通过矩形端点的积分图像值来获取的，是这样的情况:。

Sum(D)=ii1+ii4-(ii2+ii3) (1)

(2) 特征值计算

两个不同的矩形区域像素和之差，是矩形特征的特征值，通过（1）式能够计算任意矩形特征的特征值，下面以图2。1里的特征原型A为例子，来说明特征值的计算。

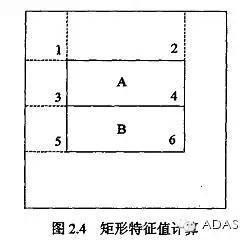
如图2.4 所示，该特征原型的特征值定义为:

Sum（A）-Sum（B）

基于（1）式来讲的话，存有如下式子，Sum(A)的值是ii4加上ii1之后再减去括号中ii2与ii3相加的和；Sum(B)的值是ii6加上ii3之后再减去括号中ii4与ii5相加出来的值。

所以此类特征原型的特征值为:

（ii4减去ii3），减去（ii2减去ii1），加上（ii4减去ii3），减去（ii6减去ii5）。

另外表示，运用积分图能够快速计算给定的矩形的所有象素值之和Sum(r)。假设r等于(x,y,w,h)，那么这个矩形内部所有元素之和等同于下面积分图里下面这个式子:。

和（范围）等于内部图像（横坐标加宽度，纵坐标加高）加上内部图像（横坐标减一，纵坐标减一）减去内部图像（横坐标加宽度，纵坐标减一）减去内部图像（横坐标减一，纵坐标加高）。

按这样来看，能够发现，矩形特征的特征值计算，仅仅是和此特征端点的积分图之间产生关联，然而和图像的坐标值并不存在关联。针对于同一类型的矩形特征而言，不论特征的尺度以及位置处于什么样的状况，特征值计算所消耗的时间均为常量，并且都决然只是基本不带有复杂程度的加减运算。其他类型的特征值计算方式与之相类似。