pg下载网站麻将胡了 如何通俗易懂地解释卷积？

卷积这个概念，在很早之前就已经学过了，然而始终都没有弄明白。教科书一般会给出定义，还会给出诸多性质，也会运用实例以及图形来进行解释，但是到底为何要如此设计，如此计算，其背后的意义是什么，常常说得含糊不清。身为一个学物理出身的人，要是一个公式给不出结合实际的直观的通俗解说（也就是背后的“物理”意义），就会觉得好像缺了些什么，感觉并非真的理解了。

教科书上一般定义函数 的卷积 如下：

连续形式：

离散形式：

先对 g 函数进行翻转，这得到了一种状态，这种状态相当于，在数轴上把 g 函数从右边褶到左边去，而这一过程，也就解释了卷积的“卷”的由来。

接着将g函数朝着n进行平移，于这点处在两个函数的对应点之间做相乘操作，随后把所得结果进行累加，此一历程便是卷积的“积”的进程。

这仅仅是于计算的手段方面针对公式予以了阐释，就数学而言挑不出毛病，然而进一步去追问，为何要先去进行翻转随后再实施平移，这般设计有着怎样的意图，依旧是有些让人难以理解。

有诸多热心网友针对卷积给出了诸多形象示例予以诠释，像卷地毯那般，又如丢骰子那样，还似打耳光这种，以及存钱这类情况等。读过之后觉着极具生动趣味性，然而仔细思索一番，仍旧感到存有某些地方尚未阐释明晰，甚而有可能会存在瑕疵，或者说还能够予以改进（对此后续小编会开展一些剖析）。

我带着问题费尽心思地想了两个夜晚，最终渐渐觉得有一些问题是想明白了的，因而就将其写出来打算跟网友去分享，以期能够共同学习并且得到提高。

明确一下，这篇文章主要想解释两个问题：

怎样去解释卷积这个用于特定概念的名词？对“卷”这个字所代表的含义该如何说明？那“积”这个字所表达的意思又是怎样的？

2. 卷积背后的意义是什么，该如何解释？

考虑的应用场景

为了更好地理解这些问题，我们先给出两个典型的应用场景：

1. 信号分析

有一个进行输入的信号f(t)，这个信号要经过一个线性系统，该线性系统的特征能够用单位冲击响应函数g(t)去描述，之后得到的输出信号会是什么呢？实际上借助卷积运算便能够获得输出信号。

2. 图像处理

将一幅图像f(x,y)输入进去，使其经过经过特定设计的卷积核g(x,y)来进行卷积处理，这样一来，输出图像便会得到各种效果，比如模糊，还有边缘强化等。

对卷积的理解

关于卷积这个名词的理解是，两个函数的卷积，其本质是，先把其中一个函数去翻转过来，接着进行滑动叠加。

先是在连续的此种状况之下，叠加所意味的是针对两个函数的乘积去进行求积分，接着在离散的这种情形当中，便是通过加权进行求解，为了达成简单起见的这个目的，就将其统一称作叠加。

整体看来是这么个过程：

多次滑动得到的一系列叠加值，构成了卷积函数。

“卷积”里的“卷”，说的是函数的翻转，是从g(t)变为g(-t)的这个环节；并且，“卷”还带有滑动的意思在其中（采纳了网友李文清的提议）。要是将卷积译为“褶积”，那么这个“褶”字就仅有翻转的意思了。

卷积的“积”，指的是积分/加权求和。

存在一些文章，仅仅着重于进行滑动叠加求和，却并未提及函数的翻转，我认为这样的情况是不全面的；有部分文章，对于“卷”的理解，实际上给出的是“积”的认知，我觉得这类文章是把事情弄混淆了。

对卷积的意义的理解：

从“积”阶段观察可见，我们所获取的叠加数值，展现为一种全局理念范畴之内的事物。以信号剖析作为实例来讲，卷积运算的最终成果，并非仅仅与当下时刻输入信号所引发的响应数值存在关联，而且还和往昔全部时刻输入信号所产生的响应情况均有关系，这其中考量了往昔所有输入所带来效果的积累状况。在图像处理这个领域当中，卷积操作所产生的结果，实际上就是将每个像素周围的，甚至是整个图像范围内拥有的像素都纳入考量范畴，进而针对当前像素实施某种加权的处理举措。那么也就是说，“积”属于全局范畴的概念，换而言之是一种“融汇”，将两个函数于时间维度或者空间维度上予以融汇。

2. 那么为何要开展“卷”呢？直接做相乘难道不行吗？依我的理解，实施“卷”（翻转）的意图实际上是施加一种限定，它明确了在进行“积”的时候是以什么作为参照的。在处于信号分析该情形下，它指明了在哪个特定的时间点的前后去开展“积”，是在空间分析的这种场景里，它确定了在哪个位置的周边进行累积处置。

举例说明

下面举几个例子说明为什么要翻转，以及叠加求和的意义。

例1：信号分析

如下图示，所输入的信号为f(t)，其是依随时间来变化的。系统的响应函数是g(t)，于图里其中的响应函数是顺着时间呈指数下降的，它实际上所具备的物理意义是如此表述的，即要是在t = 0这个时刻存在着一个输入，那么随着时间不断地流逝，此输入便会持续遭受衰减。换而言之，到达了t = T时刻的时候，原本在t = 0时刻的输入f(0)的那个值将会衰减成为f(0)g(T)。

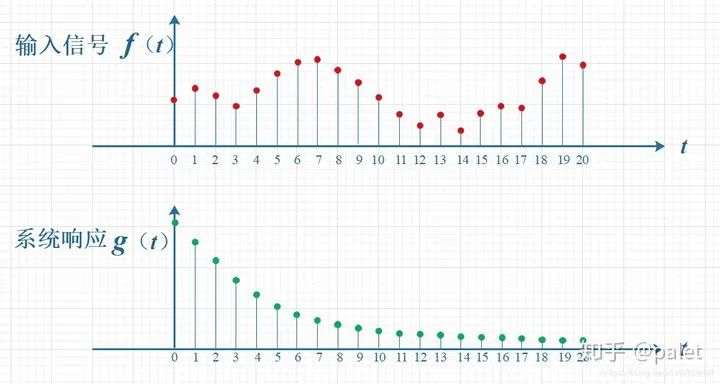
于信号连续输入的状况而言，这意味着，在每一时刻竟皆会有崭新信号进入，进而，最终输出的乃是所有先前输入信号的累积成效。就如同下面这幅图所呈现的那样，在T等于10这个时刻之时，其输出结果与图当中带有标记的区域整体存在关联。其中，f(10)鉴于它是刚刚输入的缘故，所以其输出结果理应是f(10)g(0)，而时刻t为9时候的输入f(9)，仅仅经过了1个时间单位的衰减罢了，所以产生的输出应当是f(9)g(1)，依此类推，也就是图中虚线所诠释的那种关系。将这些对应点进行相乘，之后进行累加，所得到的结果，便是T等于10时刻的输出信号值，而这个结果，同时也是f与g这两个函数在T处于10时刻的卷积值。

很明显，上边所呈现的对应关系看起来相对不太美观，呈现出一种拧巴着的状态，所以呢，我们将g函数进行对折操作，这使得它变成了g(-t)的样子，如此一来便看上去稍微美观一点了。瞧见了吧，这正是卷积为何要说“卷”，并且要进行翻转的缘由所在，这是依据其物理意义推导出来的。

上边的图，尽管没有处于拧着的状态，已然顺向过来了，然而看起来仍旧存在些许错位，所以再朝着更进一步的方向平移T个单位，这便是下边的图。它就是在本文开篇处给出的卷积定义的一种以图形方式呈现的表述：

因此，于上述计算T时刻的卷积之际 ，需予以维持的约束便是：t加上 （T减去t）等于T。这般约束的意义 ，诸位能够自行领悟。

例2：丢骰子

于本问题，即那个如何通俗易懂地解释卷积的问题里，排名处于第一位置的那位马同学，在其中举了一个相当不错的例子，下面的一些图是从马同学的文章里摘取的，在此要表示感谢，他用丢骰子这种方式说明了卷积的应用。

需解答的问题为：存在两枚骰子，将它们都投掷出去，两枚骰子所显示的点数相加起来成为4的概率是多少呢？

把两枚骰子点数加以累加，其结果等于4的情形存在三种，分别是：1加上3等于4，2加上2等于4，3加上1结果为4。

因此，两枚骰子点数加起来为4的概率为：

写成卷积的方式就是：

在这里我想进一步用上面的翻转滑动叠加的逻辑进行解释。

首先，鉴于两个骰子的点数之和是4，为了达成此约束条件，我们依旧将函数g进行翻转，随后阴影区域上下对应的数开展相乘操作，接着进行累加，这等同于求取自变量为4的卷积值，情况如下所示：

进一步，这般翻转之后，能够便利地开展推广，进而去求取两个骰子点数和为n时的概率，此概率为f和g的卷积f*g(n)pg下载通道，如下如图所示：

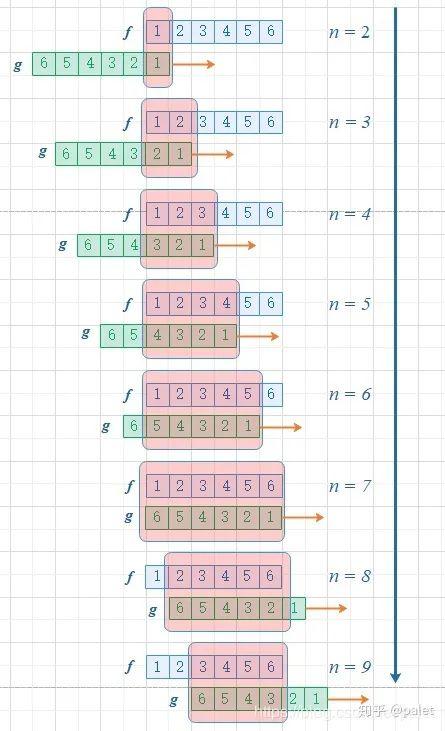
可从上图看出，函数g进行滑动，所造成的结果是点数和增大。在这个例子里，针对f与g的约束条款是点数和，它同样是卷积函数的自变量。要是感兴趣，还能够计算一番，当骰子的各个点数出现次数为均等状况时，两个骰子的点数和好使n等于7之际，概率是最大的。

例3：图像处理

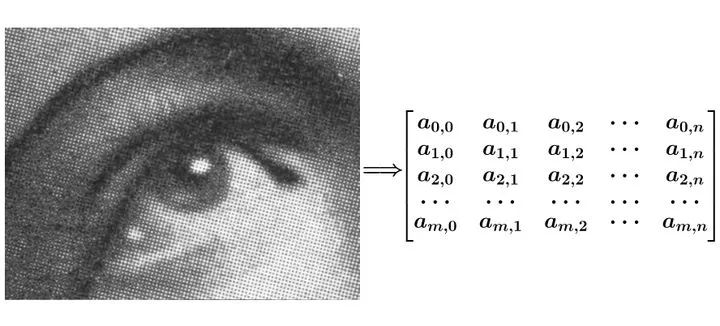
图像可以表示为矩阵形式（下图摘自马同学的文章）：

用于对图像进行处理的函数，像平滑处理，或者边缘提取处理，同样能够运用一个g矩阵予以表示，举例如下：

注意，我们在处理平面空间的问题，已经是二维函数了，相当于：

那么函数f和g的在（u，v）处的卷积 该如何计算呢？

按卷积的定义，二维离散形式的卷积公式应该是：

从卷积的定义方面来看，应当是于x以及y这两个方向上去进行累加，此累加对应着上面离散公式里的i和j这两个下标，并且该累加是没有界限的pg下载，其范围是从负无穷一直到正无穷pg下载麻将胡了A.旗舰厅进体育.cc，然而，现实的世界全部都是存在界限的，举例来说，上面所列举的图像处理函数g实际上是一个3x3的矩阵，这意味着，在除了原点附近之外的地方，其他所有点的取值均为0，将这个因素考虑进来的话，上面的公式实际上出现了退化的情况，它仅仅是把坐标（u，v）附近的点挑选出来进行计算了，所以，真正的计算呈现如下所示：

首先我们在原始图像矩阵中取出（u,v）处的矩阵：

之后把图像处理矩阵进行翻转，（此翻转颇具趣味，能有几种不一样的理解，但其作用却相等效：（1）首先沿着x轴实施翻转，接着沿着y轴施行翻转；（2）先是沿着x轴进行翻转，随后沿着y轴予以翻转），例如如下这般：

原始矩阵：

翻转后的矩阵：

（1）先沿x轴翻转，再沿y轴翻转

（2）先沿y轴翻转，再沿x轴翻转

计算卷积时：

请留意，上述公式存在一个特性，实施乘法运算的两个相对应的变量a、b的下标总和均为（u, v），其意图在于针对此种加权求和予以一种限定。这亦是将矩阵g予以翻转的理由所在。上述矩阵下标之所以如此书写并且进行了翻转，是为了能够让大家更为清晰地察觉到与卷积间的关联。如此行事的益处是利于进行推广，且利于领悟其物理层面的意义。实际于开展计算之际，皆是运用翻转之后的矩阵，直接求取矩阵内积便可行之。

以上所进行的计算，计算的对象是（u，v）处的卷积，通过延x轴滑动，或者延y轴滑动，如此这般就能够求出图像里各个位置的卷积，其输出的结果是经过处理以后的图像，所谓经过处理以后的图像指的是即经过平滑、边缘提取等各种处理的图像。

再更深入地去进行思考，在计算图像卷积之际，我们是直接于原始图像矩阵当中选取了处于（u，v）位置处的矩阵，为何要选取这个位置的矩阵呢，从本质上来说实际上是为了去满足以上所提及的约束。因为我们要计算处于（u，v）位置处的卷积，而g矩阵是一个3x3规格的矩阵，要使得下标跟这个3x3矩阵相加之后的结果是（u，v），那就只能是去选取原始图像里以（u，v）作为中心的这个3x3矩阵，也就是图中阴影区域所示意的矩阵。

假如，要是g矩阵并非3x3，换成了7x7，彼时，我们就得于原始图像里取以（u，v）作为中心的7x7矩阵展开计算。照此看来，这般卷积乃是将原始图像当中的相邻像素统统纳入考量，予以混合。相邻的区域范畴取决于g矩阵的维度，维度愈大，所牵涉的周边像素愈多。至于矩阵的设计，其决定了这种混合输出的图像与原始图像相比较，到底是变得模糊了，还是更为锐利了。

比如，像下面这样的图像处理矩阵会致使图像变得更加平滑，看上去更模糊，原因在于它对周边像素开展了平均处理。

处于如下这种状态的图像处理矩阵，会致使像素值呈现较大变化的区域相较于原先情形之下变得更加显著，能够对边缘的凸显起进一步增强作用，然而对于像素值变化较为平缓的区域而言不会产生任何影响，从而达成将图像边缘提取出来的目标：

参考资料

关于慧维智能

2019年6月，慧维智能医疗科技有限公司宣告成立，该公司本职所谋之事，乃对智能医疗产品进行研发、生产以及售卖 ，此其所在之领域。我们的核心成员，全部是从四面八方来的，他们俱皆出自全球顶尖的科研机构，亦或是世界五百强企业。慧维智能，是以其在“人工智能”以及“边缘计算”这两个领域当中所具备之内具自主性的核心技术当作驱动力的，其目标旨在为全球范围内的医疗机构，给予那种具备“高水准、低成本、好体验”这些特性的医疗产品和相关服务业，借此最大程度地去协助医生，抬高其诊疗水平，提升其诊疗效率。