pg下载 理科自学方法指导，第二讲，以高中物理牛顿定律之公式学习为例

从理科自学方法指导开始，讲到前面首次提及的第一讲，我们选取高中物理里牛顿定律当中的概念学习作为例子，阐述了针对自主学习理科概念所运用而行之有效的方法。

于所有学科知识进行深度学习时，如果仿照这样的一个流程来学习，即先是概念，接着是公式，随后是例题，跟着是讲述概念、公式以及例题相互的关联联系，再是举一个例子有多种解法，然后是多个题目归结为一类典型，之后进行拆解要正向推导也要逆向推导，再之后要总结并反思，最后是建立思维模型，那么都能够保证彻底掌握，通过方法类推，做到举一反三，进而触类旁通。

而深度理解“概念，公式，例题”三大基石是核心关键。

讲彻底掌握公式的方法，就在今天，我们来讲，先吃透了概念内涵，再掌握公式的学习方法，如此，方能扫平后续学习的道路，以高中物理牛顿定律公式的具体学习实际作为例子！

具备自主学习能力的提升，做到自身去推导公式，充分弄清楚其前因后果，这对于后续的例题研习，解题训练而言，会有着极大的助力。

这个话语指出了自主学习的关键精华所在，即从那种记住结论转变成构建知识，公式的自己推导，恰恰是在彻底理解概念之后的自然拓展以及实际验证pg下载，它凭借逻辑作为链条，把零散的知识要点串联成为牢固的网络。

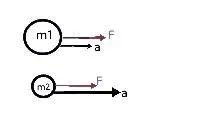
牛顿定律核心为F=ma以及它的衍生公式，以此作例子，我们要进行展示，怎样通过自己去推导，达到“懂来龙去脉”这个结果。

第一阶段：从核心概念到核心公式——F=ma 的“诞生”

牛顿第二定律本就并非依靠更基本公式作“推导”所得，它属于实验定律，是牛顿针对大量实验现象予以归纳和概括的成果。我们所进行的“推导”，实际上是对其定义属性以及逻辑脉络加以理解。

1. 从概念出发，建立定性关系：

概念1，此概念源自第一定律，力乃是致使物体运动状态发生改变的缘由，而物体运动状态发生改变也就是产生加速度。

存在这样一个概念2，它是基于实验事实得出的，对于同一物体而言，所受到的力越大，那么其加速度就越大，也就是a与F成正比（a ∝ F），而不同的物体，当受到相同的力时，质量越大，加速度越小，即a与1/m成正比（a ∝ 1/m）。

逻辑综合：将两个比例关系结合，得到 a ∝ F/m。

2. 引入比例系数，定义力的单位：

要写成等式， 让F等于k乘以m乘以a， 这里k指的才是比例系数嘛。

关键的自主定义环节，为了达到简化的目的，我们做出这样的定义，是那种能让 1kg 质量的物体获取 1m/s² 加速度的力，被规定为 1 牛顿（N）。

在进行涉及代入特定定义的计算时，当质量等于1千克，加速度等于1米每二次方秒，力等于1牛时 ，来操作计算比例系数k ，即通过1等于k乘以1乘以1从而得到k等于1。

结论：因此，在SI单位制下，公式简化为 F = m a。

用于领悟的要点是，这般“推导”能使你清楚知晓，F=ma 这种简洁形态，源自我们针对力的大小的界定方式，它并非一个纯粹的数学定理，而是物理关系与人为约定的精妙融合，是这样的，没错吧。

第二阶段：从核心公式到运动学桥梁——自主推导“来龙去脉”

这正是彰显自主学习巨大作用那种情况。我们怀着能动性运用F=ma把力学与运动学进行连接。

例1：从 F=ma 到动量定理

1. 起点：F = m a

重温加速度的定义之时，a被定义为dv除以dt。将其进行代入之后，F等于m乘以dv除以dt。

假设质量m不发生改变之情况，能够把它移进微分号的里面，此乃基于微分知识，得出F等于d(mv)除以dt的形式。

4. 定义新物理量：令 p = mv，称为动量。

获得新定理：F等于dp除以dt，也便是“合力等同于动量的变化率”。此乃牛顿第二定律的更为普适的形式（在质量发生变化之际同样适用，就像火箭那般）。

6. 积分的形式是，两边针对时间t进行积分，也就是，∫ F dt ，等于进行积分的∫ dp ，其结果是Δp ，而Δp 又等于mv₂ 减去mv₁。

左边，一个被称作冲量，也就是 (I) 的量值，它是由 ∫ F dt 来表示的，而这个量值体现的是力针对于时间所产生的累积效应。

取得动量定理，I等于Δp，也就是物体遭受和外力的冲量等同于其动量的变动。

在这一串推导之中是一个悟道点，通过它进行推导，你不但“发明”了动量概念，还“发明”了有关冲量的概念，而且你对力在时间方面上的累积效果进一步加强了理解效果，这种累积效果就是改变动量，上述知识为解决碰撞类问题且为解决打击类问题提供了全新的工具，并且是更加强大的工具。

例2：从 F=ma 到动能定理

1. 起点：F = m a

我们期望去明白力于空间里的累积成效，进而展开对空间累积的探寻，两边与一小段位移 dr 进行点乘运算。或是使用一维形式 ds 来进行运算，即 F · ds。

3. 借助加速度跟速度的关联，也即 a 等于 dv 除以 dt，还有 v 等于 ds 除以 dt，来开展关键的“微分变换”：

F与ds的乘积，等于m乘以dv与dt的商再乘以ds，等于m乘以ds与dt的商再乘以dv，等于m乘以v乘以dv。

4. 积分的过程是，针对整个过程来进行积分，这个过程是从位置 1 开始到位置 2 结束，在此期间速度由 v1 变化到 v2。

对从一到二的区间进行积分，F与ds的积分结果，等于对从v一到v二的区间出发，m乘以v与dv的积分结果，而这个结果又等于二分之一乘以m再乘以v二的平方，减去二分之一乘以m再乘以v一的平方。

5. 定义新物理量：

左边：∫ F ds 称为功 (W)，是力对空间的累积效应。

右边：(1/2)mv² 定义为动能 (Ek)。

计算得出动能定理，其表达式为W = ΔEk，这意味着，针对物体而言pg下载麻将胡了A.旗舰厅进体育.cc，合外力所做的总功，等同于物体动能的改变情况。

7. 悟道要点：这样的推导会使你一下子就明白过来，力作用在空间之中所产生的累积效果也就是那个做功，它能够改变的是动能。它可以十分完美地去解释为何“匀速圆周运动时的向心力不会做功”，原因是力一直都是垂直于位移的，根据W=0，所以动能便不会改变。

第三阶段：运用推导出的“来龙去脉”指导解题

现在，你拥有了一个清晰的“决策树”：

面对一个力学问题，如何选择公式？

1. 分析问题焦点：

若问题关联到时间，以及速度出现变化，还有碰撞情况，那么便要优先去考虑动量定理，也就是I等于Δp。

当问题关联到位移，以及速度大小出现变化，还有高度产生变化的时候，那么就要优先去考虑动能定理，也就是W等于ΔEk，或者是功能原理。

那是否意味着，所涉及的问题，关乎瞬时关系，以及加速度，还有运动细节，这种情形下，就一定要运用牛顿第二定律，也就是F=ma，再结合运动学公式来解决呢？

例题对比（一个斜面滑块问题）：

应用F等于ma这个公式时，要进行受力情况的分析，去求出合力的大小，进而算出加速度的值，最后运用运动学公式去求解时间以及位移。整个过程步骤繁多，需要详细清晰地知道各个细节。

借助动能定理，仅需晓得初速度以及末速度，明确高差，直接得出，重力所做的功加上摩擦力所做的功pg下载渠道，等于末动能减去初动能，一步就能达成速度的求解，忽略掉中间所经历的过程。

自主推导带来的根本性优势：

深知其内在深意，且永远不会忘却，那公式乃是你自身亲自“发觉”的，并非通过背诵得来的。

你明晰动量，动能，功，冲量这些概念的“血缘关系”，它们皆源于F=ma这一母体，知识成网，触类旁通。

能在完成解答题目的行为时，迅速地辨认出问题的内在本质所在，挑选出最为高效的定理来运用，而并非是毫无头绪地胡乱尝试各种公式，做到灵活地进行选用，直接命中关键之处呐！

4. 拥有“元学习能力”，掌握了“从基本定律推导衍生定理”之法，你于学习电磁学、量子力学等全新领域之际，能够主动去搭建库仑定律与电场能之间的关联，以及薛定谔方程与守恒量之间的联系。

具备实质意义的自主学习，是要将自身视作知识的“发现者”，同时还要把自身当作知识的“编织者”。

以牛顿定律为起点，通过自主推导这条逻辑之链，你将：

自 F=ma 作为起始种子，先产生动量强悍的枝干，再生长出动能有力的枝干，接着生出功有成效的枝干，随后冒出冲量有作用的枝干等强劲枝干，最终汇聚构建成经典力学的参天大树。

这棵树，它的根基十分牢固，枝干相互连接在一起，任凭风雨也无法将其摧毁。在此之后，无论是什么样的例题以及习题，统统都只是这棵树上的一片叶子而已，你始终能够清晰地看清它所连接的脉络。而这无疑就是“学会推导，搞懂来龙去脉”所带来的终极自由与力量。

欢迎关注分享，持续跟进学习交流更精彩！