pg下载网站麻将胡了 勾股定理学习教案

知识梳理：

识结构框架图：

拼图法

探索勾股定理

直角三角形三边得关系——勾股定理

方法1：角

直角三角形的判定

探索勾股定理 方法2：边

求几何体表面两点之间的最短距离

勾股定理的应用 在直角三角形中求未知边

其他

1.勾股定理：

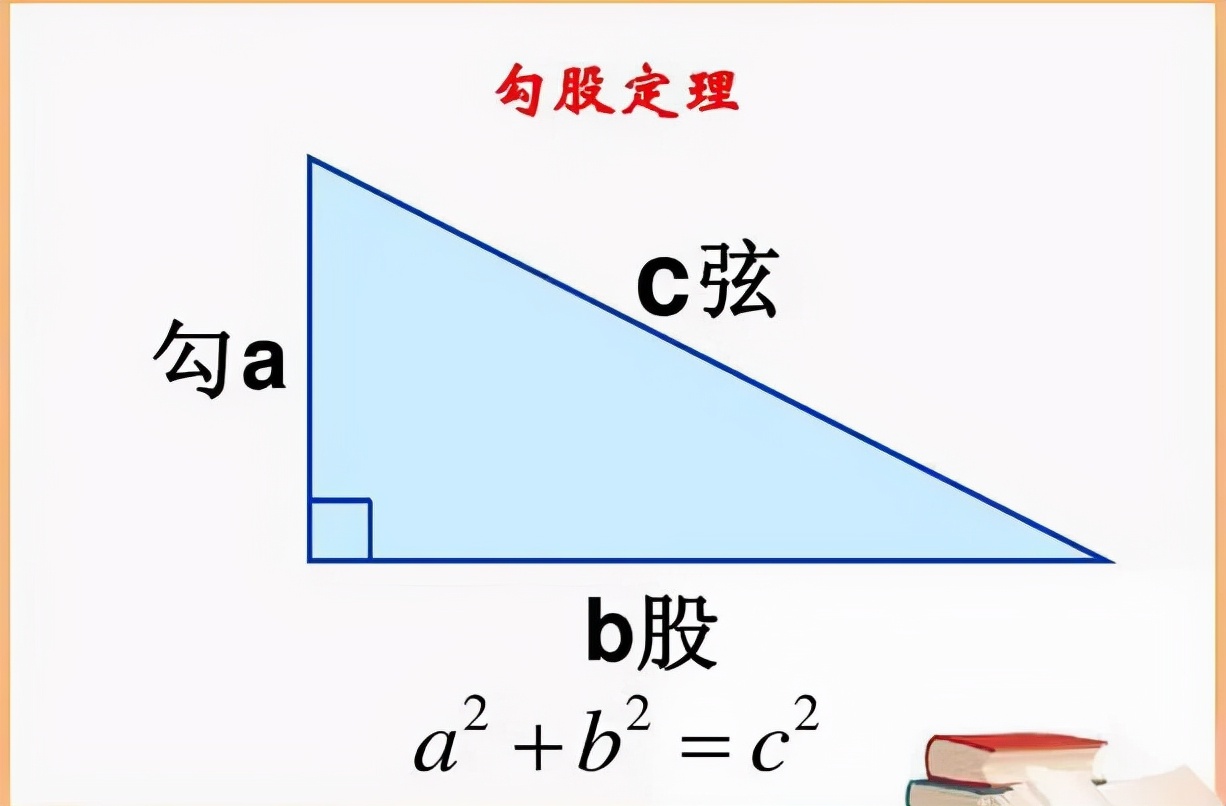
（1）有一个三角形，它是直角三角形，其两直角边长度的平方之和等于斜边长度的平方。也就是说pg下载，对于任意一个直角三角形而言，要是它的两条直角边分别是a、b，斜边是c，那么必定会有。

这就是勾股定理．

（2）勾股定理应用的前提条件是在直角三角形中．

（3）由于

所以，c大于a，同样道理，c大于b，也就是，直角三角形的斜边大于这个直角三角形里的每一条直角边。

2.勾股定理逆定理

存在这样一个命题，其内容为若三角形的两条边的平方和等于第三边的平方，那么这个三角形就是直角三角形 ，此命题是勾股定理的逆定理 ，它可助力我们判定三角形的形状 ，能为依据边的关系去解决角的相关问题提供全新的方法 ，该定理的证明运用的是构造法。

有两个命题，在这两个命题里，有这样一种情况，第一个命题的题设是第二个命题的结论，并且第一个命题的结论又是第二个命题的题设，在这种情况下，这两个命题被叫做互逆命题。要是把其中一个称做原命题，那么另一个就被叫做它的逆命题。

若一个定理的逆命题经证明为真命题，那它亦是一个定理，这两者定理称作互逆定理，其中一个被叫做另一个的逆定理。

3.勾股定理的证明：

教材证明勾股定理采用的是拼图方法，勾股定理的证明方法存在多种，先是运用拼图方式，随后借助面积相等来证明勾股定理。改为叹号！

在证明勾股定理之际，采用若干全等的直角三角形pg下载麻将胡了，将它们拼合成一个规则的图形，随后凭借大图形的面积等同于几个小图形的面积之和，展开化简整理，从而得到勾股定理。

勾股数：

4.勾股数：满足

的三个正整数，称为勾股数．

说明：

① 个数必须是正整数，例如：2.5、6、6.5满足

，但是它们不是正整数，所以它们不是够勾股数．

② 组勾股数扩大相同的整数倍得到三个数仍是一组勾股数．

③平日里常常运用于解题的勾股数，能够起到提升做题速度的作用，像这样的勾股数有pg下载通道，3，4，5；6，8，10；5，12，13…。

5.勾股定理的应用

（1）在不规则的几何图形中，通常添加辅助线得到直角三角形．

（2）在运用勾股定理去处理实际问题之际，勾股定理跟方程进行结合，乃是解决实际问题时常会用到的办法，其关键之处在于，要从题目里面抽取出勾股定理这么一个数学模型，进而画出精确无误的示意图，还要领会数形结合思想在其中的应用。

（3）常见的类型，①勾股定理在几何里的应用，透过勾股定理去求几何图形的面积，以及有关线段的长度。

②有这么个由勾股定理演变出来的结论，是这样的，讲的是有一个直角三角形，分别以它的三边为边长向外作出正多边形，然后呢，以斜边作为边长的那个多边形，其面积等于拿直角边当作边长的多边形的面积之和。

其中之一是勾股定理针对实际问题所用之处为，用勾股定理的相应数学模型去处理现实世界里的实际状况，以此来解决实际问题。

首先，勾股定理存在于数轴上表示无理数的应用之中。其次，借助勾股定理能够将一个无理数予以呈现。再者，把该无理数表示成为某种直角三角形的斜边。最后，此直角三角形的直角边是两个正整数。