用最简单的例子让零基础的你轻松理解遗传算法

遗传算法

概     述

遗传算法，亦称GA，起源于20世纪70年代，由美国学者John holland所提出。这一算法基于生物在自然界中的进化法则进行设计。它是一种计算模型，旨在模拟达尔文的生物进化论中的自然选择和遗传学原理，进而通过模仿自然进化过程来寻找最佳解决方案。此算法运用数学手段，借助计算机模拟计算，将问题求解流程转化为类似生物进化中染色体基因的交叉与变异等步骤。在处理较为繁杂的组合优化问题时，相较于诸多传统优化算法，它往往能更迅速地实现较为理想的优化效果。遗传算法在组合优化、机器学习、信号处理、自适应控制以及人工生命等多个领域得到了广泛的应用。

01

大致了解

遗传算法是启发式算法家族中的一员，当我们试图理解启发式算法时，不妨将其与枚举法进行对比。以一个简单的例子来说，当我们试图找到函数f(x)的最大值时，常用的做法是求导数以确定极值点。然而，大家可能也清楚，还有一种较为原始的方法，那就是枚举法。若x的取值范围限定在0到1之间，且对x的最大值求解的精度要求为0.01，那么我们便可以将0到1区间内，以0.01为间隔的所有可能解（包括0.01、0.02、0.03等，直至0.98、0.99和1.00）逐一代入函数f(x)，通过比较它们的函数值，从而确定其中的最大值。此时，使得f(x)达到最大值的x值即为问题的最优解，而该最大值即为f(x)的函数值。然而，该方法的求解速度十分缓慢；为了克服这一难题，众多专家依据不同领域的独特原理，诸如生物学中的遗传规律、鱼类和蚂蚁的群体行为、冶金领域的退火技术等，将这些理论巧妙地融入求解过程，旨在提升求解的效率。在持续探索以寻求最佳方案的过程中，借助这些原理，我们能够使探索变得不再盲目，转而依照既定规律去探寻最佳方案，从而显著提升求解的效率，使得我们能够更加迅速地锁定f（x）的最优解。

总的来说，为了更好地把握遗传算法的精髓，我们首先可以形成这样一个基本观念：遗传算法实际上是对枚举法的一种优化和提升。

02

简单算例

需要计算函数f(x)＝x＋10*sin(5*x)＋7*cos(4*x)在区间[0,9]内的最大值。

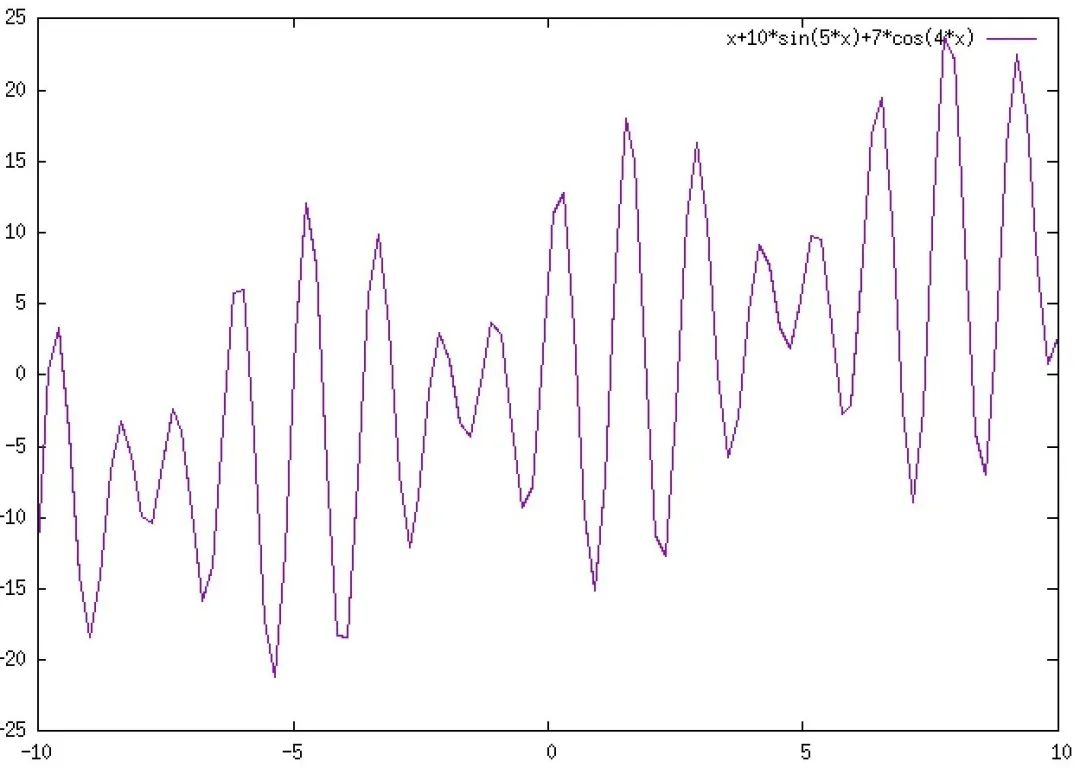
p．s．  f（x） 函数大致图像如上图

遗传算法，简称GA，其运作基于“适者生存”和“优胜劣汰”的基本法则，它是一种模仿自然界中生物选择和遗传规律进行的随机搜索算法。遗传算法模拟了人工种群的演变历程，它运用了选择、交配和变异等策略，在每轮迭代中持续保留一批候选个体。经过多轮的循环迭代，种群在若干代之后，理论上其适应度会趋向于达到近似最优的状态。

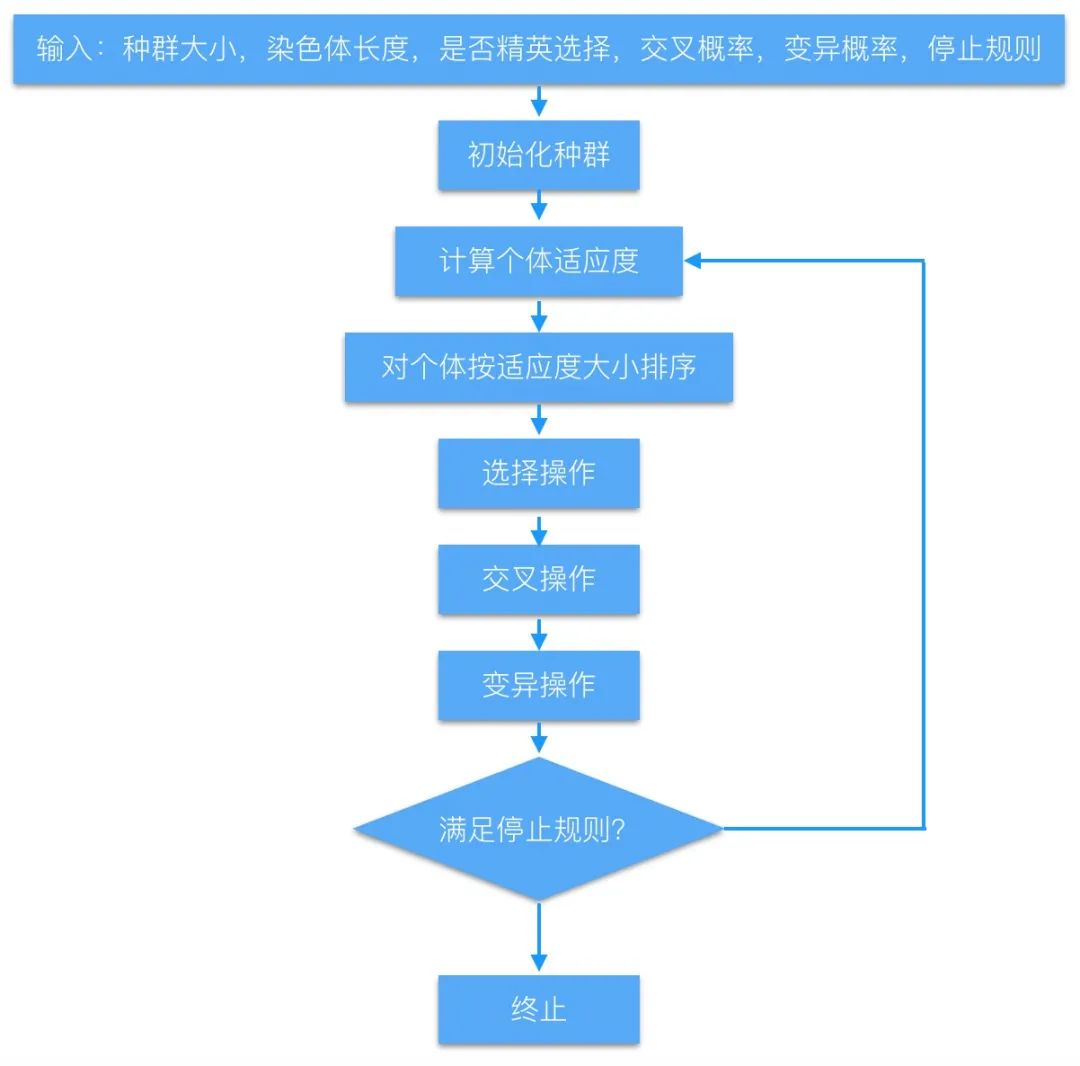
p．s．  遗传算法流程图如上图

组成：

编码 －＞ 创造染色体

个体 －＞ 种群

适应度函数

遗传算子

• 选择

• 交叉

• 变异

运行参数

• 是否选择精英操作

• 种群大小

• 染色体长度

• 最大迭代次数

• 交叉概率

• 变异概率

编码与解码：

实现遗传算法的第一步就是明确对求解问题的编码和解码方式。

对于函数优化问题开元ky888棋牌官网版，一般有两种编码方式，各具优缺点。

直接以实数对基因进行编码，这样的做法便于理解且省去了解码步骤，然而，它可能导致过早地达到收敛，进而陷入局部最优解的困境。

二进制编码具有很高的稳定性，同时拥有丰富的种群多样性，然而它所需的存储空间较大，并且解码过程复杂，理解起来也相对困难。

对于求解函数最大值问题，我一般选择二进制编码：

以函数f(x)等于x加10倍的正弦函数五倍x再加7倍的余弦函数四倍x，定义域为从0到9的区间为例。

若将求解的精确度设定为小数点后四位，那么x的解集范围可以被细分为（9减去0）乘以（1乘以10的4次方），即90000个等间隔的部分。

2的16次方小于90000，而90000又小于2的17次方，因此表示这些解至少需要17位二进制数。换言之，每个解的编码形式为一条17位的二进制序列。

一开始，这些二进制串是随机生成的。

此类二进制序列可映射为一条染色体序列，而该染色体序列的长度恰好是17个单位。

对于此类染色体，我们该如何将其还原（解码）成位于区间[0,9]内的具体数值呢？

对于本问题，我们可以采用以下公式来解码：

x 等于 0 加上染色体上的十进制数乘以（9 减去 0），然后除以（2 的 17 次方减去 1）得到的十进制数。这表示将一个二进制数值转换成十进制数值的过程。

一般化解码公式：

对于函数f(x)，当x位于区间[lower_bound, upper_bound]内时，其值计算如下：x等于lower_bound加上染色体中decimal部分的值乘以(upper_bound - lower_bound)除以(2的chromosome_size次方减1)。这里的lower_bound代表函数定义域的下限。

upper＿bound： 函数定义域的上限

chromosome＿size： 染色体的长度

借助该公式，我们便能够有效地将二进制染色体序列转换成位于0至9区间的十进制实数解。

个体与种群：

『染色体』表达了某种特征，这种特征的载体，称为『个体』。

在本次实验中，我们需解决一元函数的最大值求解问题。针对这一问题，个体可通过上一节所构建的染色体来进行表示，而每个个体均包含一条染色体。

众多此类个体汇集而成的一个群体，其内涵可解释为一个沿x轴分布、范围介于0至9之间的一维点集。

适应度函数：

在遗传算法领域，个体（即解）的优劣程度是通过适应度函数的数值来衡量的；在本特定问题中，函数f(x)即为我们所说的适应度函数。

适应度函数值越大，解的质量越高。

适应度函数充当遗传算法演化的核心动力，同时也是自然选择过程中评判优劣的唯一准则，其设计需紧密贴合求解特定问题的具体需求。

遗传算子：

我们期待构建一个群体，其中每个成员对应的函数值均与f(x)在区间[0,9]上的最大值极为接近。然而，起初这个群体或许并不出色，这是因为组成个体的染色体序列是随机形成的。

如何让种群变得优秀呢？

不断地进化

每次物种演变都力求保留种群中杰出的成员，剔除那些不适宜的个体，并在杰出的个体间进行染色体的互换，同时，部分个体还可能发生变异现象。

每一次种群进化的过程开yunapp体育官网入口下载手机版，都会孕育出一个最优秀的个体。而这一种群历代中最杰出的个体，或许正是函数f(x)所能达到的最大值所对应的那个定义域内的特定点。

若物种持续不断地进化，那么终将寻得最理想的答案。然而，现实情况是，我们所拥有的时间并不充裕，往往在获得一个看似满意的解决方案后，便会停止进化的过程。

对于给定的种群，如何赋予它进化的能力呢？

首先是选择（selection）

在繁衍过程中，研究者们会从前代群体中挑选出多对表现优异的个体，每一对这样的个体被称作一对父母。这些父母会将自身的基因遗传给下一代，这一过程持续进行，直至新生的个体数量达到预设的种群上限。

在选择操作前，将种群中个体按照适应度从小到大进行排列

运用轮盘赌式的挑选机制（尽管存在其他挑选手段，例如竞标赛制），每个个体被选中的几率与它们适应度函数的数值高低呈正相关关系。

轮盘赌的选法带有偶然性，这可能导致优质个体被淘汰，因此引入精英策略，直接选取上一代的最优个体。

其次是交叉（crossover）

两个将要发生交叉的染色体（分别来自父母）会按照一定的交叉概率（cross_rate）以特定方式相互交换它们的部分遗传信息。

采用单点交叉法，也可以使用其他交叉方法

最后是变异（mutation）

染色体的变异是依据变异概率（mutate_rate）来决定的，这一概率决定了染色体发生变化的程度。

采用单点变异法，也可以使用其他变异方法

通常情况下，交叉率较高，而变异率则非常低。例如，在寻找函数最大值的问题中，我设定的交叉率为0.6，而变异率仅为0.01。

遗传算法坚信，两条杰出的父母染色体进行交配，孕育出卓越后代的几率较高；相对而言，变异产生卓越后代的概率极小，尽管如此，偶尔也有可能瞬间变异出极其出色的后代。这种现象与自然界生物进化的规律相吻合。

03

算例代码

这个例子是我学习遗传算法时用到的，它相对简单开yun体育app入口登录，便于理解。若您对此仍有疑问，欢迎通过后台与我们取得联系。此外，我还附上了该算例的代码，适用于matlab版本。

请访问以下链接获取所需资源：https://pan.baidu.com/s/1rvhtA4kaxQuJTmndiVS71Q，输入提取码bfrr即可。