初中几何模型——网红模型12345模型

一、模型结论

结论表明，一个锐角的正切值为1/2开元ky888棋牌官方版，另一个锐角的正切值为1/3，这两个锐角的度数相加恰好等于45度。

符号表示：

α、β都是锐角，则

图形表示：

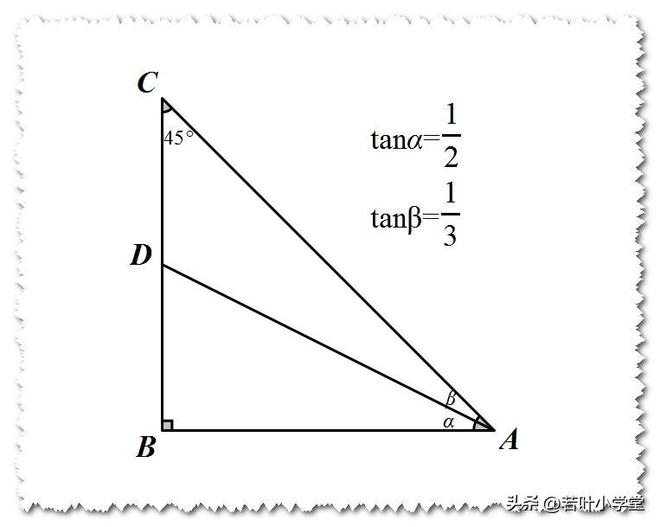
2、倍角结论：

若某锐角的正切值为1/2，则该锐角的两倍角的正切值应为4/3。

若某锐角的正切值为三分之一，则该角的两倍角的正切值应为四分之三。

若某锐角的正切值为4比3，则该锐角一半角度的正切值为1比2。

若某锐角的正切值为3比4，则该锐角的一半的正切值为1比3。

若某锐角的正切值为2，则该角之半角的正切值可计算为(√5-1)除以2。

图形表示：

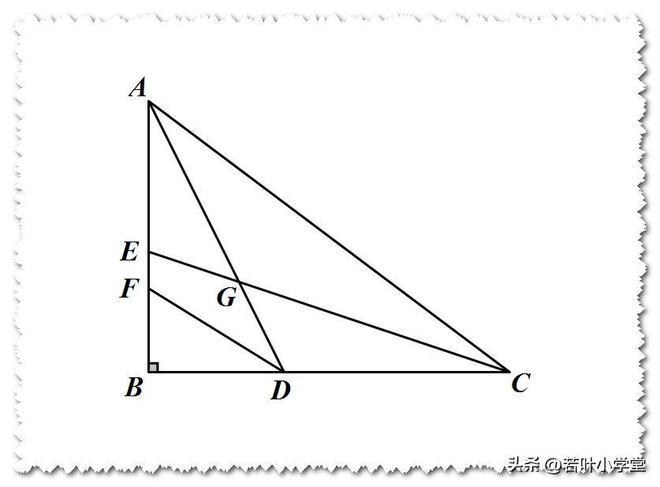
如图，在RTABC中，AB=3，BC=4，AC=5

AD平分∠BAC，CE平分∠ACB，DF平分∠ADB

在三角形BCE中，角BCE的正切值为1/3；在三角形BAD中，角BAD的正切值为1/2；而在三角形BDF中，角BDF的正切值为(√5-1)/2。

此图同样能够展示角度关系的结论：三角形CAG的切线值为1/2，三角形ACG的切线值为1/3，而角CGD的度数为45度。

之所以命名为12345模型，是因为该模型与数字12345之间存在着紧密的联系。

二、模型证明

1、和角结论

原命题与这样一个事实等价：该锐角减去45°后，其正切值为1/2，而该锐角的正切值本身则为1/3。

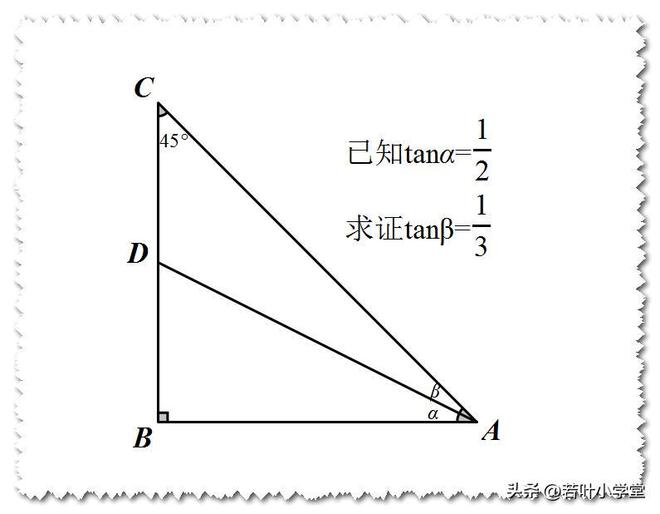
过点D作DE⊥AC于点E

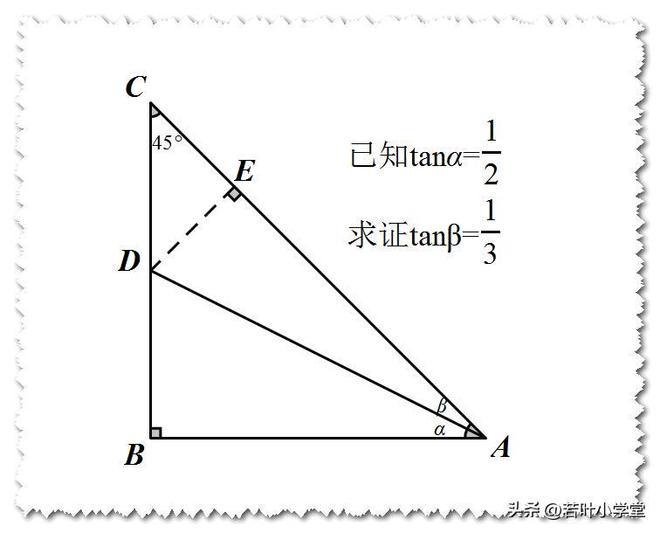
设AB=BC=2m，则AC=2√2m，BD=CD=m

CE=DE=√2m/2，AE=3√2m/2

∴tanβ=1/3

2、倍角结论

以①③为例

①如果一个锐角的正切值是1/2，那么它的二倍角的正切值是4/3

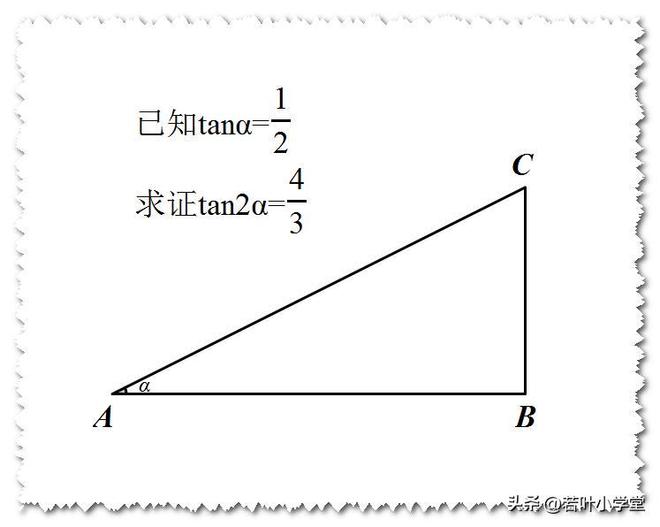
在AB上取点D，使AD=CD，连接CD，则∠BDC=2α

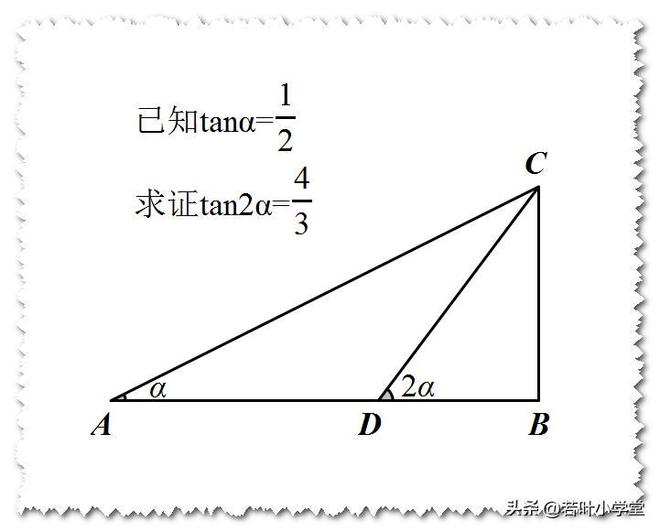
根据证明，若设BC的长度为m，BD的长度为x，那么AB的长度将是2m，同时AD的长度等于CD的长度，均为2m减去x。

在RTBCD中，由勾股定理，得

x^2+m^2=(2m-x)^2 解得 x=3m/4

∴tan2α=m/(3m/4)=4/3

③如果一个锐角的正切值是4/3，那么它的半角的正切值是1/2

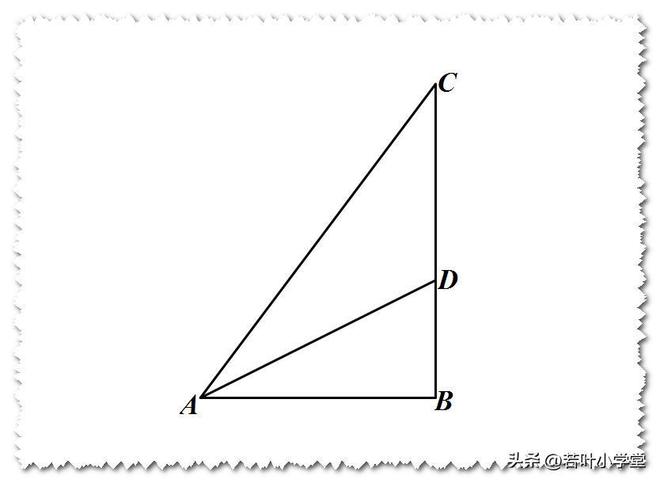
图中所示开yunapp体育官网入口下载手机版，RTABC内，直角位于点B，且∠B的度数为90度；同时，线段AD将∠BAC一分为二；此外，线段AB的长度为3，而线段BC的长度为4。

求证tan∠DAB=1/2

证明：过点D作DE⊥AC于点E

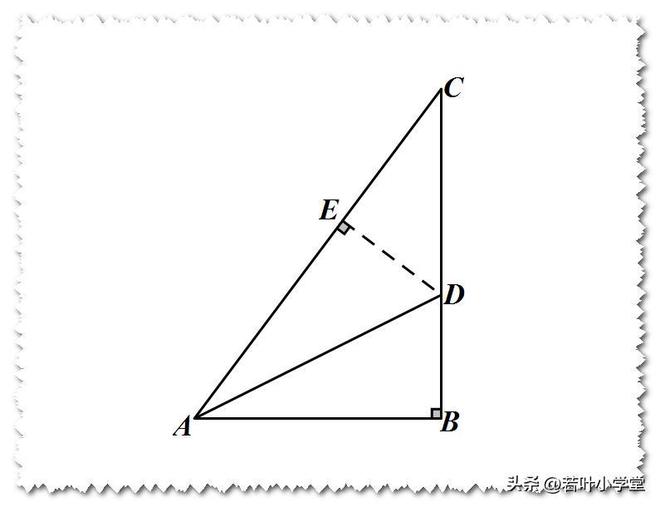
由勾股定理，得 AC=√(3^2+4^2)=5

易证BAD≌EAD(AAS)

∴AB=AE，DB=DE

设DB=DE=x，则CD=4-x，CE=2

在RTCDE中，由勾股定理，得

x^2+2^2=(4-x)^2 解得x=3/2

∴BD=3/2，tan∠DAB=1/2

②④⑤都可以用类似的方法证明

三、模型应用

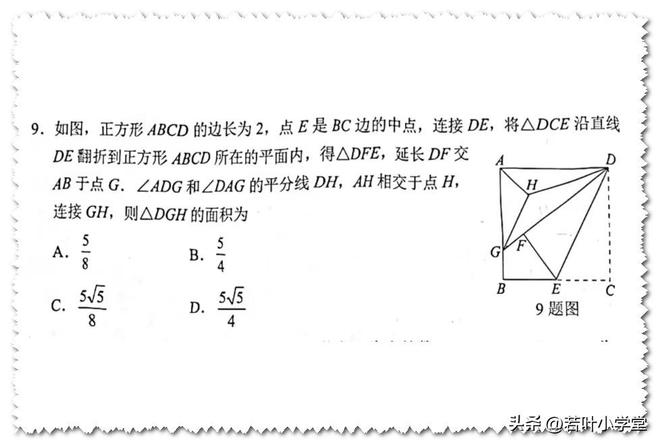
在点H处，HI垂直于DG，交于点I；在点J处，HJ垂直于AD；在点K处，HK垂直于AG。

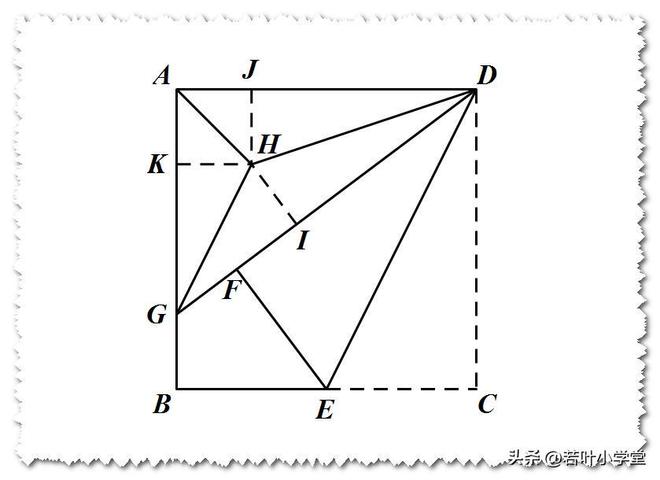
∠EDH=45°，tan∠EDF=1/2

根据12345模型，我们可以得出tan∠HDG的值为1/3，同时tan∠ADG的值为3/4。

∴AG=3/2，DG=5/2

∵H是角平分线交点 ∴HJ=HK=HI

∴SAGH:SADH:SDGH=3:4:5

因此，SDGH的计算公式为5除以（3加4加5），而SADG的计算过程则是将5除以12，再乘以1/2，再乘以3/2，最后乘以2，结果为5/8。

四、小结

该模型主要适用于选择和填空题型，针对适合该模型的题目，12345模型通常能快速给出答案，而对于那些或许不特别快捷的题目，它也能提供一种额外的解题思路。

在中考模拟考试中，任何能够通过12345模型进行解答的问题，都可以运用课堂上学到的知识来解决。

12345模型并不像部分网红博主所宣称的那么神乎其神开元棋官方正版下载，同时也并非如某些博主所贬低的“无用”，对于那些学习能力强、有额外精力同学，我建议他们去学习，因为多掌握一门技能并不会造成负担；而对于学习基础一般的学生，则应根据自己的能力适度学习。