数学之美 | 斐波那契数列
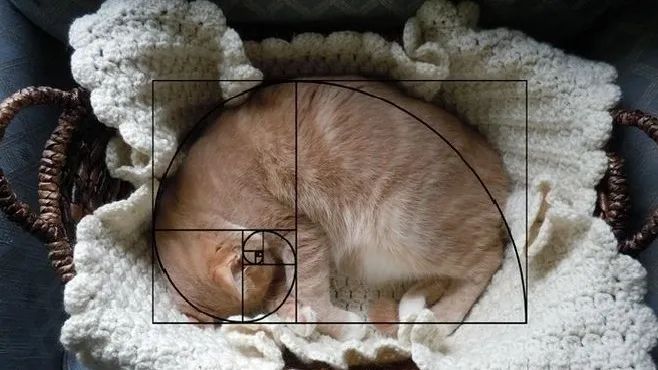
我们一同模仿猫叫,反复发出喵喵喵喵喵的声音,喜爱小猫咪的人明白它们为何如此迷人吗?接下来,借助一个极其优美的数列,让我们深入探索小猫咪所展现的迷人之处。
[id_788477701]
这个数列由意大利数学家列昂纳多•斐波那契在1202年提出,他通过“兔子繁殖”的例子来介绍它,因此它也被称为兔子数列,有时也被称作黄金分割数列,人们认为这是大自然创造的一种完美比例,如今它在现代物理、准晶体结构、化学等多个学科中都能找到实际用途。
这个数列是这样定义的:1,1,2,3,5,8,13,……,其中从第三个数开始,每个数都等于它前面两个数相加的结果。根据这个规律,可以总结出一个递推公式,如果用Fi表示数列的第i个数,那么Fi就等于F(i-1)加上F(i-2)。

01
提出背景--兔子繁殖问题
有一对初生的兔子,从第三个月起,它们每个月都会繁殖出一对新的兔子,而新出生的兔子从第三个月开始也遵循同样的繁殖规律,每个月产生一对后代。假设兔子不会死亡,遵循这种繁殖模式,到第十个月的时候,总共会有多少只兔子。

02
自然之奇--红花绿树
树木的新成长枝条需要一段自我发展期,才能接着长出新的枝丫。因此,一棵树苗隔一段时间就长出一条新枝;到了第二年,新枝会进入休养期开元ky888棋牌官网版,而老枝还会继续长出新的枝条。从那以后,老枝和已经休养一年的枝条会同时生长,而当年新长出的枝条则在第二年进入休养期。

如果持续这样发展,一棵树在各个年份形成的枝条数量就会形成斐波那契数列,这种模式在生物学中被称为“鲁德维格定律”。

03
自然界中的花
自然界中,花是斐波那契数列的体现之一。花朵的构造方式与树枝相似,并且许多花朵的花瓣数量符合该数列,比如1,2开yun体育app入口登录,3,5,8等数字。以雏菊为例,其单朵花的花瓣数有时能达到21,34,55或89片。




此外,还有向日葵,这种植物的花盘里存在两条螺旋状纹路,一条是朝顺时针方向旋转的,另一条则是朝逆时针方向旋转的,而且它们相互交缠在一起。

这些交替上升下降的数值并非固定不变,常常出现在13与21、34和55、55和89以及89和144这样的几对数字中,每一对都由斐波那契序列里紧挨着的两个数构成。
这种布局方式能帮助植物最大限度地吸收光线和利用气流,从而提升其繁殖成效,它其实是在漫长岁月的演变过程中,通过自然筛选逐渐形成的,大自然的表现确实令人惊叹。

04
建筑之美--金沙铁塔
建筑设计师们格外钟爱0.618这个数值,古埃及的宏伟金字塔,欧洲巴黎的著名圣母院,还有近代法国的埃菲尔铁塔,以及希腊雅典的巴特农神庙,这些著名建筑都蕴含着黄金分割的原理。

Porch of Maidens,雅典卫城
然而,古希腊的建筑杰作帕特农神庙,依然鲜明地体现了黄金比例所产生的视觉愉悦。虽然缺乏明确史料证明古人是有意设计成这样,不过该神庙的正立面上,其长方形的宽度和长度比例,非常接近1.618与1的比率。

帕特农神庙黄金比例分割图
吉萨金字塔是古埃及最出名的建筑,人们普遍认为它始建于4600年前,时间早于古希腊的帕特农神庙。这座金字塔的设计巧妙地运用了黄金分割的法则,比如,从锥体侧面三角形顶部到底部的垂直距离,同方形底座边长一半的比例,非常接近人们所说的黄金比例。

古埃及金字塔黄金比例分割图
历史文献证实中世纪时期建筑中应用了黄金分割,当时的大型教堂常以规整多边形作为核心构造形态,而哥特式玫瑰窗便是这类设计的杰出代表。此后在文艺复兴阶段,意大利的学者Luca Pacioli和建筑师Leon Battista Alberti也积极倡导运用黄金分割。

中世纪教堂顶的哥特式玫瑰窗
当代一些建筑也运用了黄金分割的原理,例如法国埃菲尔铁塔,其高度达到300米,塔身和平台的布局协调,分别设有地面以上57米、115米以及276米三个观景台。其中115米处的平台,其上部结构与整体的比例为185与300之比,计算结果约等于0.617,这个数值和黄金分割点0.618非常接近。

法国埃菲尔铁塔
因此,埃菲尔铁塔第二层平面的坐标十分贴近整座建筑高度的最优分割点,同时这也是塔身结构从四条支柱向外扩展转为向内聚拢的转换节点。

05
数学之谜--斐波那契数列与黄金分割
斐波纳契弧线也称作黄金螺线,首先,这种曲线依据两个端点来绘制,比如从最低点到最高点线段上的两个位置,其次,三条弧线都以第二个点为圆心画出,并且分别与趋势线上的斐波纳契比率38.2%,50%以及61.8%相交,再者,斐波纳契弧线能够标示出潜在的价格支撑位和阻力位,此外,在图表分析中,斐波纳契弧线经常和斐波纳契扇形线一起使用。这些线的汇合之处便是支撑位与阻力位所在位置。需要留意的是,弧形交点和价格走势线会随图表数值区间调整而变动,由于弧线属于圆周构成部分,因此其构成方式始终如一。
黄金螺线
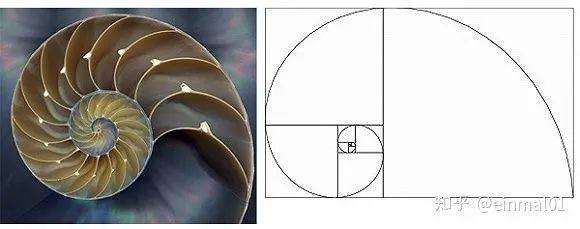
运用黄金螺旋在摄影中,可以增加获得卓越照片的可能性。与静态的三分法相比开yun体育官网入口登录app,黄金螺旋为我们观察画面时提供了动态的轨迹。它始终在两个界限之间转动,从上往下,能够使作品的布局更加多样化。



总而言之,斐波纳契数列在日常生活中随处可见,尽管其中一些已被我们察觉,不过或许还有许多尚未被我们发掘,与斐波纳契数列紧密相连的黄金比例被广泛运用,但仍有空间需要我们深入探究。
存在于自然界的数学之美不胜枚举
蝴蝶翅膀的对称生长
理想情况下雪花的科克曲线
银河系螺旋状的旋臂
数学与我们无处不在的结合
闪耀着无限的光芒






