卷积和CNN - 哔哩哔哩
卷积网络跟卷积并不等同,卷积网络仅是借用了卷积的运算方式的一种网络构造,并非完全等同的概念。
卷积:
卷积是一种数学操作,能够融合两个函数所包含的内容,通过线性方式实现信息整合。
卷积是泛函分析里的一种运算,用于由两个函数f和g得到一个新函数,这种运算本质上属于积分变换,它反映的是函数f和g在翻转和平移后重叠区域的函数值乘积,再对重叠区域的长度进行积分的结果。
数学表达式如下:
CNN:
卷积神经网络CNN属于前馈神经网络,主要承担图像识别和计算机视觉方面的工作,其构造思路源自生物视觉系统,目的是模仿人类进行视觉信息处理的过程。
中心观念在于,经由一连串的卷积运算(本质上为互相关运算)与降采样处理,神经网络逐步识别输入信息的内在属性,再借助全连接部分完成识别或预测任务。
CNN在视觉识别、物体定位、图像创作等方面表现出色,已成为深度学习探索的关键构成部分。
卷积神经网络里的卷积层运用的是交叉相关,而非常规的数学卷积过程,因此卷积核无需进行180度翻转。
卷积核和输入图像的每个点都做元素级乘法,接着把所有乘积加起来,得到一个值。这个核在图像上移动,对每个新位置都重复上述计算,得出该位置的输出值。在整个运算中,卷积核不会发生翻转。
数学领域里的卷积运算,一般需要对卷积核进行半圈翻转,但在卷积神经网络中,实际运用的是互相关运算开元棋官方正版下载,所以无需对卷积核进行翻转处理。
如何理解卷积?
一个最直观的案例是消化模型:
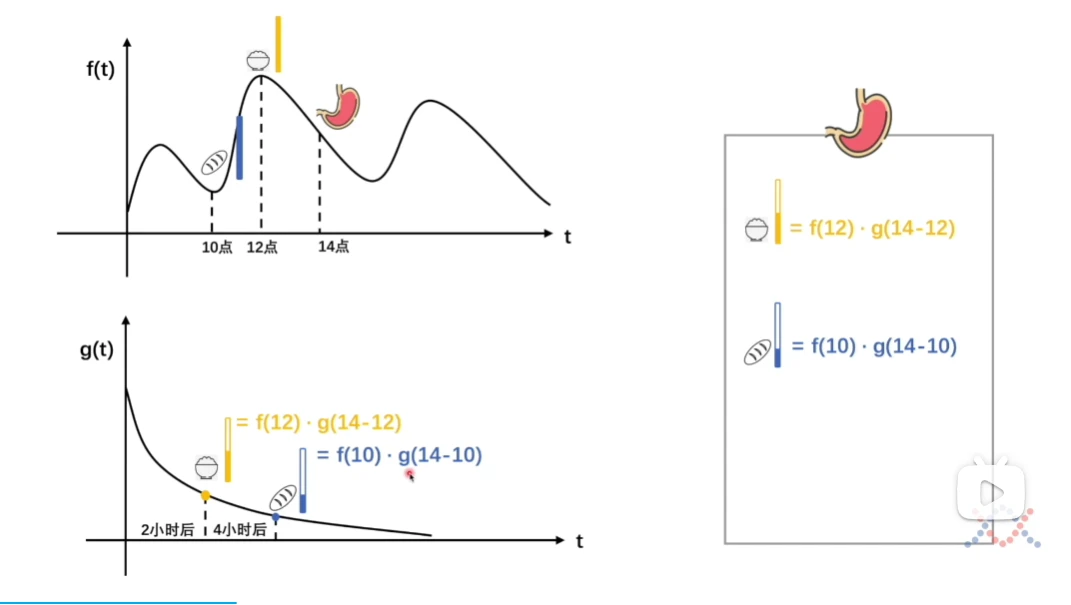
我们设定f(t)为衡量进食量随时间变化的表达式,由于时间推移导致食物不断被消化,g(t)则反映单位食物在时间流逝中剩余量的变化规律,我们旨在推算14时胃中食物的实际存量,考虑到摄入的食物持续消耗,必须逐时核算从先前时段至14时的食物损耗状况,例如12时食物到14时的留存程度可表述为f(12)乘以g(14-12),10时食物对14时的影响则为f(10)乘以g(14-10)开元ky888棋牌官方版开元ky888棋牌官网版,依此类推,需将各项影响累计,即转化为积分形式,该形式体现从零时到任意时刻进食行为对当时食物总量留存的影响程度。我们将范围拓展到全体,就能表示出卷积公式了。
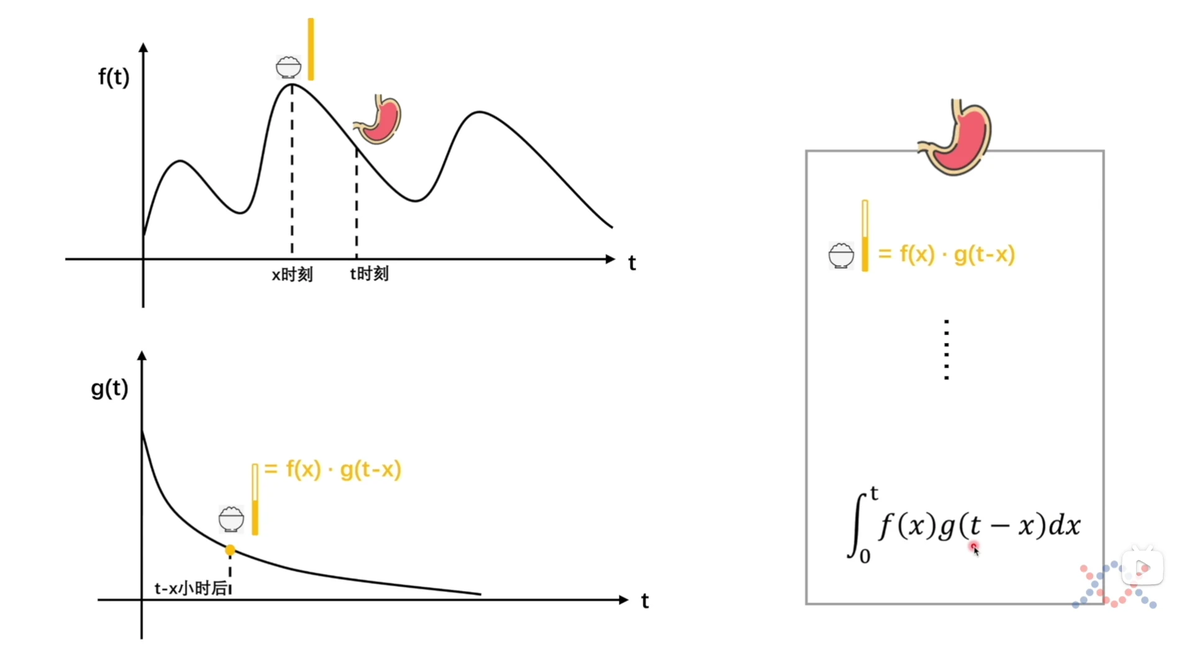
将g(t)进行旋转并展开,能够使其与f(t)逐项匹配,卷积的过程就是先完成旋转展开,再进行逐项相乘。
因此,卷积的第一个理解形式就是:
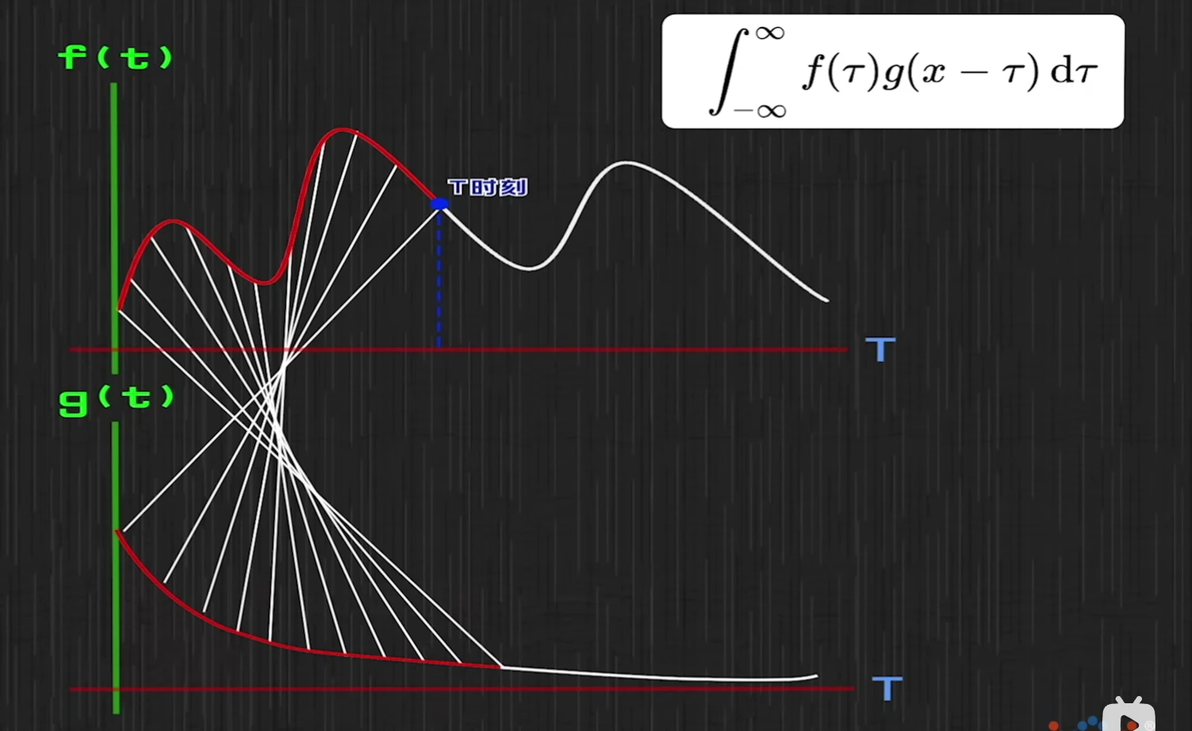
当某个装置的入力波动不定,而其出力却保持平稳时,能够借助卷积运算来求得该装置的积累量
在卷积神经网络对图像的处理流程如下:
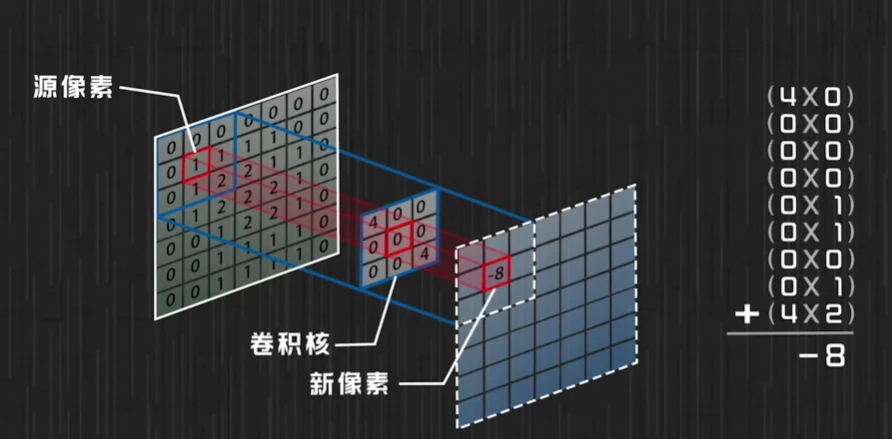
使用一个滤波器,初始图像从左上部分开始,提取与滤波器尺寸相等的像素区域,执行元素相乘再求和的运算,从而生成新图像的步骤。这种乘加运算并非卷积的核心概念,两者之间毫无关联性。
卷积的第二种理解:
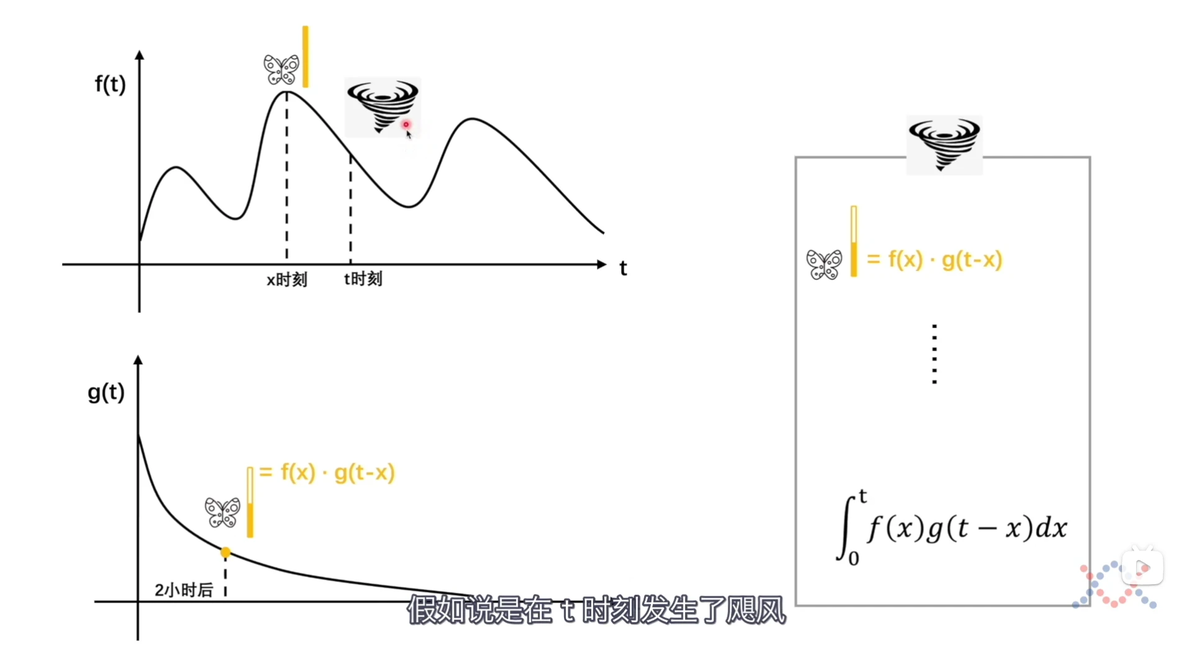
我们设g(t)代表一个事件对另一个事件的作用力,比如一只蝴蝶扇动翅膀,每只蝴蝶的行为互不影响,该作用力会逐渐减弱,在特定时间点t,f(t)表示有多少只蝴蝶进行了该行为,两者结合后的结果,就是从时间零到t期间,对t时刻的累积效应。
通过分析卷积神经网络的运作方式,可以明白:周围区域的所有像素对中心像素的作用效果,就是卷积运算的全部意义,而那个字母t,其实代表的是空间上的位置差异,并非时间概念,卷积核本质上就是那个g(t)函数,它描述了这种位置差异如何影响中心像素。

通过卷积运算可以确定一个函数:f值乘以g值等于所有f值与g值对应位置差值的乘积之和
卷积核的相对位置如右图所示,而左图中f函数的位置与右图中g函数的位置正好相反,我们必须旋转g(m,n)的坐标,这样它才能和f函数完全匹配。这种做法似乎是让卷积神经网络和卷积运算产生了关联。然而在具体计算时,我们使用的是交叉相关的方法,直接通过矩阵内积来计算结果,因此不需要进行坐标旋转。
f函数定义了周围像素点产生的影响,而g函数规定如何影响。
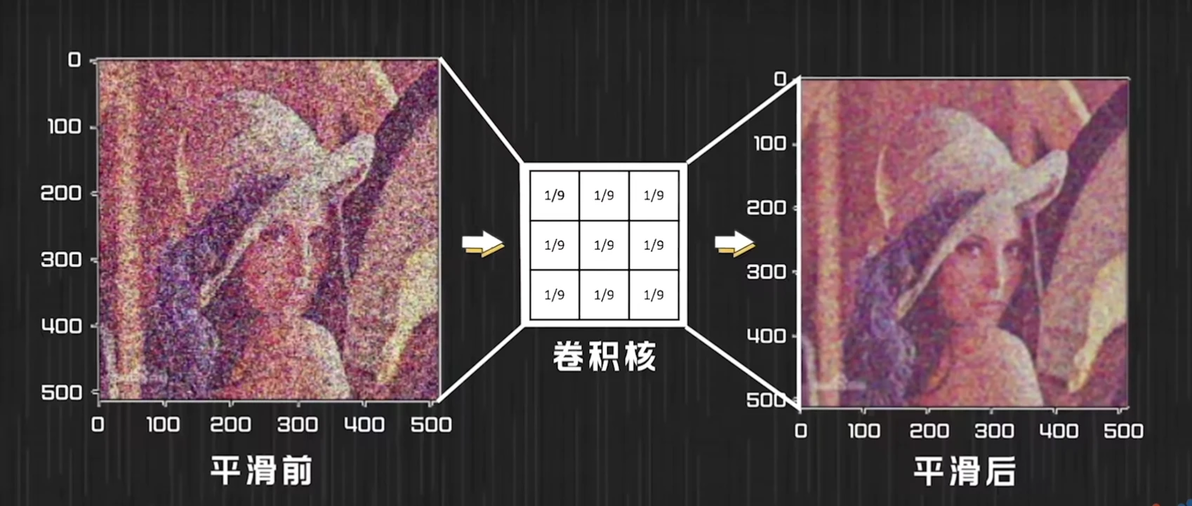
应用:高斯模糊(平滑卷积核)
第三种理解:(过滤器提取特征)
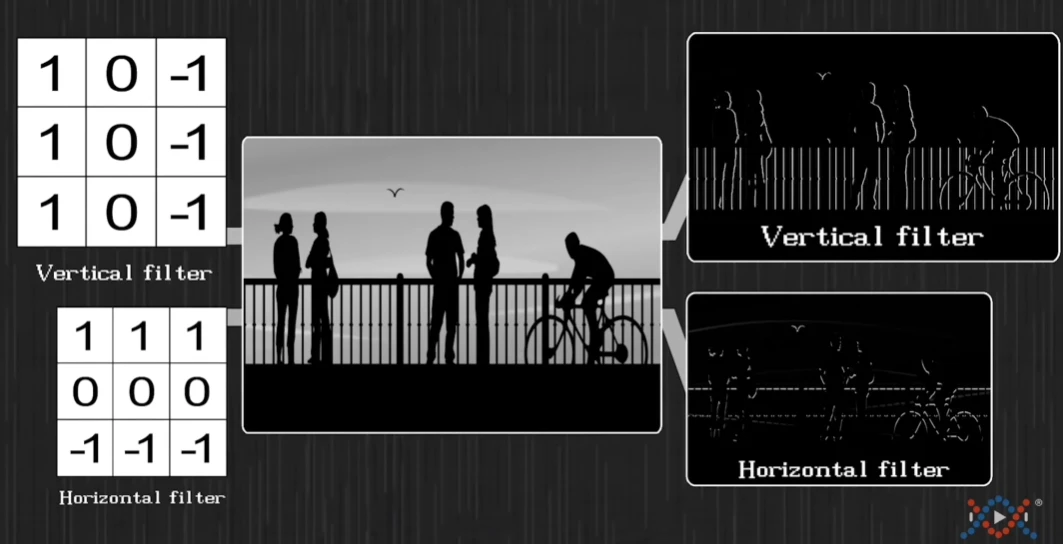
卷积核的数值用来试探邻近的像素点,其目的是为了挑选图像中的显著部分。
这个专栏和其中的文章旨在记录个人对深度学习知识的掌握历程,内容未声明为原创,仅作为个人学习资料使用。




