对卷积的定义和意义的通俗解释
对卷积的困惑
卷积这个理论,过去曾经接触过,却始终未能理解透彻。书本里通常会有它的说明,列举诸多特性,还会借助案例和图像来阐明,然而究竟为何要这样构建,这样运算,其深层目的何在,往往解释得含糊不清。从事物理学研究的人,若一个方程式无法提供贴合现实、易于理解、直白明了的阐释,也就是其内在的“物理”内涵,就会觉得有所缺失,认为并未真正掌握。
教科书上一般定义函数
的卷积
如下:
连续形式:
离散形式:
并且说明了,首先对g函数实施反转操作,相当于在数轴上把g函数从右侧向左侧折叠过来,这就是卷积中“卷”字含义的出处。
接下来将g函数平移至n的位置,在此处对两个函数的相应点进行相乘,再把所有乘积结果加在一起,这就是卷积运算中“和”的部分。
这个仅从运算角度对公式作出说明,在数学层面无可指摘,然而深入探究,为何要先将对象颠倒再进行位移,这种安排的缘由实在难以明了。
幸运的是,互联网这个强大的工具,特别是知乎、CSDN这类平台,汇聚了许多热心的网友,他们用很多生动形象的比喻来阐释卷积的概念,例如卷地毯、投掷骰子、拍打耳光、储蓄等,可以参考知乎上两个广受关注的问题,那里有众多网友的精彩解答,参与讨论的人非常多。
怎样用简单的话说明卷积的原理呢,这个问题在知乎上有人讨论过,链接是https://www.zhihu.com/question/22298352。
这种数学运算为何被称作「卷」运算?,它的名称来源是什么?
读完后觉得相当活泼有趣,不过深入琢磨,仍然觉得部分内容不够明晰,甚至可能存在不足,或者尚有提升空间(这些方面后面我会进行探讨)。
经过两夜的反复思索,许多困惑逐渐清晰,于是将心得记录下来,希望与网友交流探讨,一起进步。若有欠妥之处,敬请指出批评指正。
明确一下,这篇文章主要想解释两个问题:
卷积这个术语如何进行阐述?“卷”具体指代什么含义?“积”又代表什么意义?
2. 卷积背后的意义是什么,该如何解释?
考虑的应用场景
为了更好地理解这些问题,我们先给出两个典型的应用场景:
1. 信号分析
一个输入信号f(t)进入一个线性系统,这个系统的特性由单位冲击响应函数g(t)表征,那么最终的输出信号会是什么样子?实际上,运用卷积运算能够准确计算出这个输出信号。
2. 图像处理
输入一张图像f(x,y),使用定制化卷积核g(x,y)实施卷积运算后,所得图像会呈现模糊化,边缘突出等不同变化。
对卷积的理解
对卷积这个概念的认识:所谓两个函数的卷积,其核心是先将其中一个函数进行颠倒,接着进行移动式的相加处理。
连续情形里,叠加意味着对两个函数相乘的结果进行积分运算,离散情形下则是进行带权重的求和,为了方便起见,就通称为叠加。
整体看来是这么个过程:
颠倒,接着是平移,然后是堆砌,再次平移,接着堆砌,再平移,然后堆砌,如此反复进行
多次滑动得到的一系列叠加值,构成了卷积函数。
卷积中的“卷”表示函数的镜像,即将 g(t) 转变为 g(-t) 这一步骤;
卷积的“积”,指的是滑动积分/加权求和。
部分文章仅着重论述滑动累加,却忽视了函数的镜像,这种表述不够周全;另一些文章对“卷”的阐释实质上是“积”,存在概念混淆的情况。
对卷积的意义的理解:
从“积累”的演变中可以看出,我们获得的累加结果,是一个整体性的认知。以信号处理为例,卷积的成效不仅取决于当前时刻输入信号的反馈数值,还取决于此前所有时段输入信号的反馈情况,顾及了过往所有输入所产生的综合影响。图像处理里,卷积处理的结果,就是把每个像素周围的,乃至整个图像的像素都纳入考量,对当前像素实施某种加权处理。由此可见,“积”体现的是全局性,或者说是一种“融合”,将两个函数在时间或空间维度上进行交织。
为什么需要执行“卷”这个操作?直接相乘不可以吗?我的看法是,进行“卷”(翻转)其实是为了施加一种限制,它明确了在计算“积”的时候应该以什么为基准。在信号处理的情境下,它规定了在哪个特定时刻的上下进行计算“积”,在空间处理的情境下,它规定了在哪个具体位置的范围进行累加操作。
举例说明
下面举几个例子说明为什么要翻转,以及叠加求和的意义。
例1:信号分析
输入信号为 f(t) ,该信号具有时间依赖性。系统响应函数为 g(t) ,如图所示,该函数随时间呈指数形式减小,其物理内涵在于:若在 t=0 时刻施加输入,则该输入会随时间逐渐减弱。具体而言,当时间达到 t=T 时,原本在 t=0 时刻的输入 f(0) 将会衰减至 f(0)g(T) 的水平。
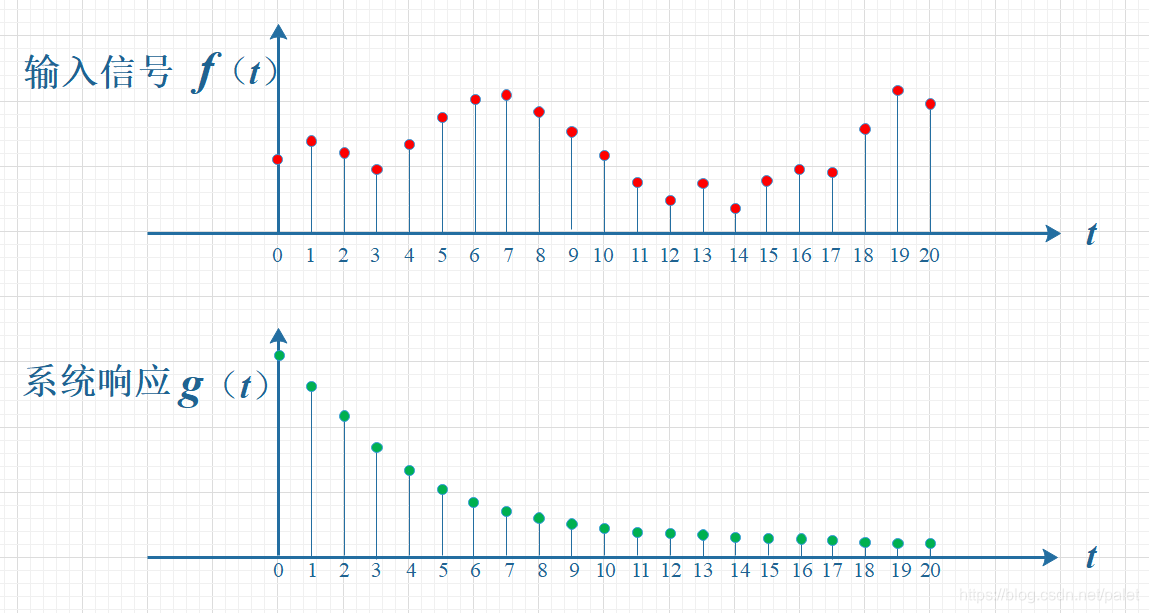
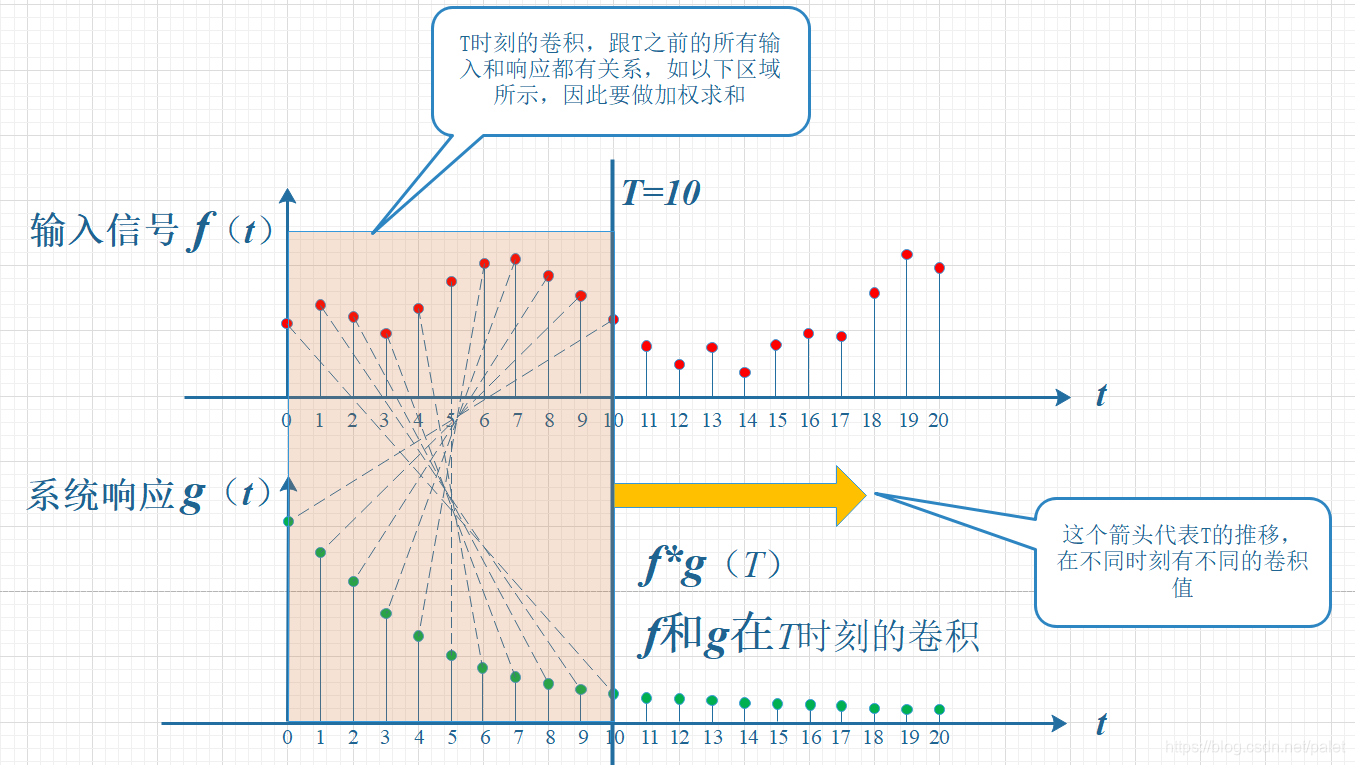
因为信号不断接续传送,每时每刻都有新数据传输进来,因此,最终得到的结果是所有先前输入数据的综合作用。根据图像展示,在第十个时间点,最终响应值与图中特别标注的部分密切相关。那个f十的值,由于是刚刚输入的,因此它的输出值应当是f十乘以g零,而时间点九的输入f九,仅仅经历了一个时间段的减弱,因此它生成的结果应该是f九乘以g一,依次类推,也就是图中虚线展示的关联。这些点逐一相乘并累计,便得到T等于十时的输出数值,这个数值同时是函数f与g在T等于十时进行的卷积运算所得结果。
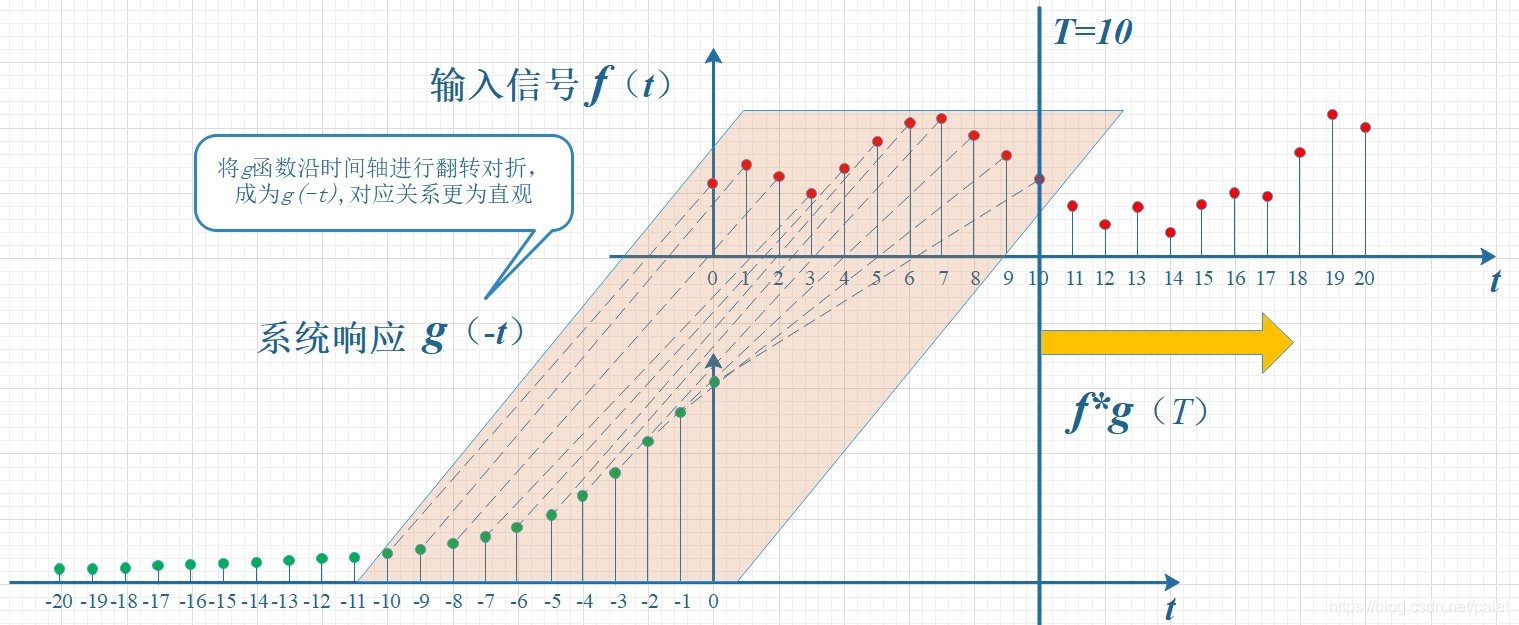
这个对应关系显得有些杂乱,是颠倒的,因此,我们让g函数进行镜像处理,变为g(-t),这样看起来就顺眼了,注意到了吗?这就是卷积之所以要“卷”,需要反转的道理,这是从它的实际意义中得出的结论。
图像虽然已经调顺,但仍有轻微偏差,因此需要再移动T个单位,得到下图所示,这个图形是对本文开头卷积定义的一种视觉化说明:
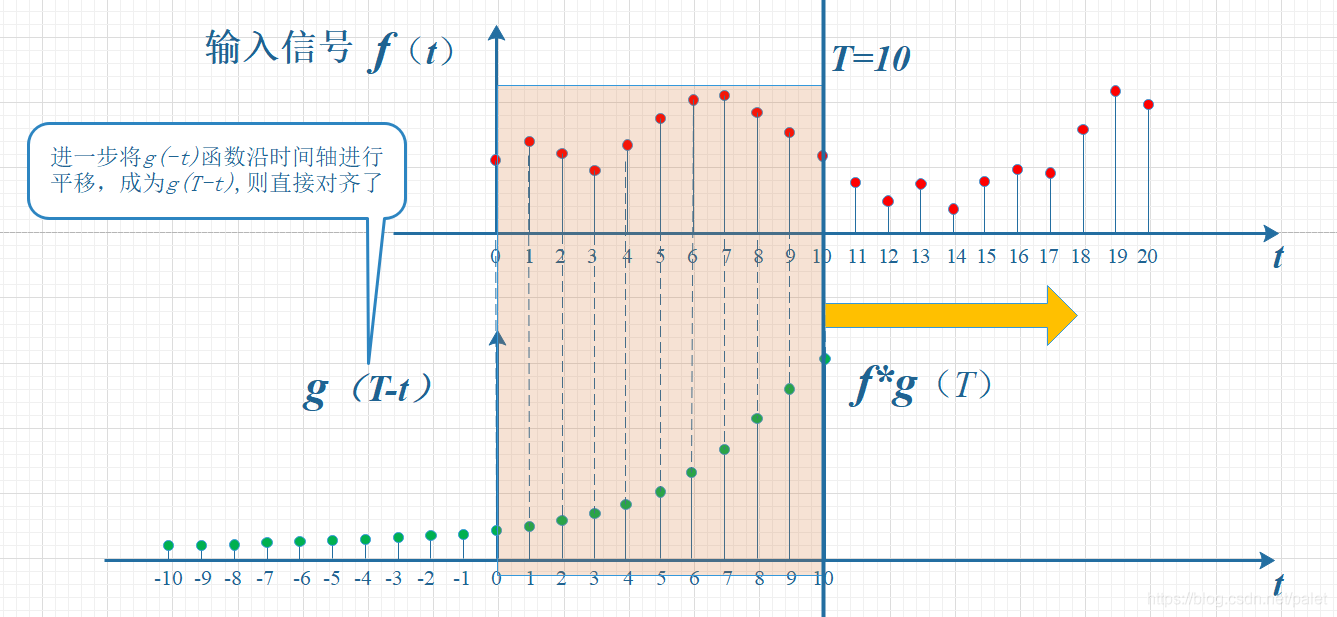
因此,针对T时刻的卷积运算,需要坚持的规则是:t加上T减去t,结果等于T。这个规则的作用,读者可以自行领悟。
例2:丢骰子
关于知乎上那个关于卷积如何简单说明的问题,马同学给出的答案里,有一个通过掷骰子来解释卷积应用的故事,这个例子非常精彩,很多图片都选自他的文章,在此特别致谢
需要计算的是:存在两枚骰子,当它们同时被掷出时,两个骰子显示的数字之和等于4的可能性有多大?

考察一下,两颗色子数值合计为四的组合存在三种情形:第一是数字一与数字三的组合,第二是数字二与数字二的组合,第三是数字三与数字一的组合
因此,两枚骰子点数加起来为4的概率为:
写成卷积的方式就是:
在这里我想进一步用上面的翻转滑动叠加的逻辑进行解释。
首先,由于两个骰子的点数总和为4,需要满足这一条件,因此我们仍然将函数 g 进行反转处理,接着将阴影部分上下对应的数值相乘,最后将所有乘积结果累加起来,这实际上等同于计算自变量为4时的卷积值,具体效果如图所示:
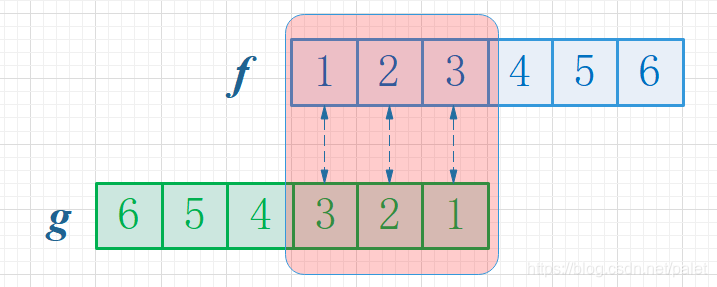
接下来,经过这种转换,能够便捷地拓展来计算两个骰子点数合计为 n 的几率,这就是函数 f 和 g 的卷积 f*g(n),具体示意图展示如下:
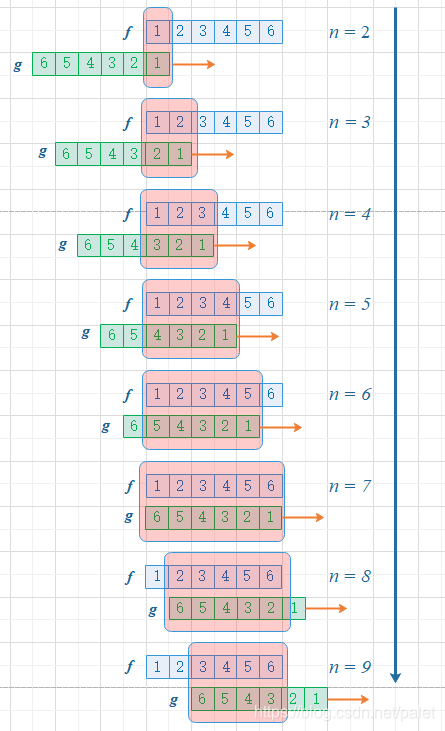
根据图像可以知道,函数 g 的移动,导致点数总和增加。这个案例中,对 f 和 g 的限制就是点数总和,它也是卷积运算的输入值。如果对概率感兴趣的话,可以计算一下,当两个骰子每个面出现的几率相同,点数总和为 n=7 时,出现的可能性最大。
例3:图像处理
还是借鉴知乎上有关卷积通俗说明的问题里马同学所举的例子,图像能够看作是矩阵形态,具体内容见马同学文章中的附图
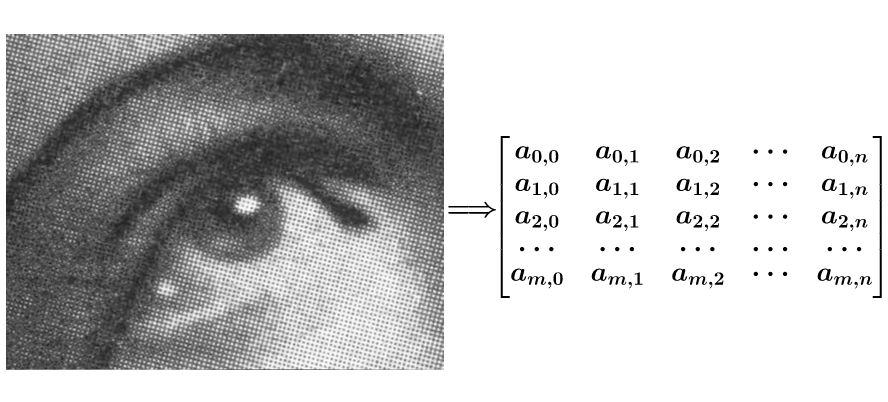
图像的平滑操作或边缘检测功能,同样能够通过一个g矩阵来描述,例如:
注意,我们在处理平面空间的问题,已经是二维函数了,相当于:
那么函数f和g的在(u,v)处的卷积
该如何计算呢?
按卷积的定义,二维离散形式的卷积公式应该是:
卷积的界定方式涉及x轴和y轴两个维度上的求和运算,这与前面离散公式中的i和j两个索引相对应,其理论范围是无限延伸的,从负无穷大到正无穷大。然而,现实场景往往存在限制条件。以之前提到的图像处理函数g为例,它本质上是一个3x3的方阵,表明除了中心位置以外,其它所有位置的计算结果都为零值。鉴于这一情况,先前给出的公式实际上已经简化了,它仅仅选取了坐标(u,v)周边的点来进行运算。因此,实际的操作流程是这样的:
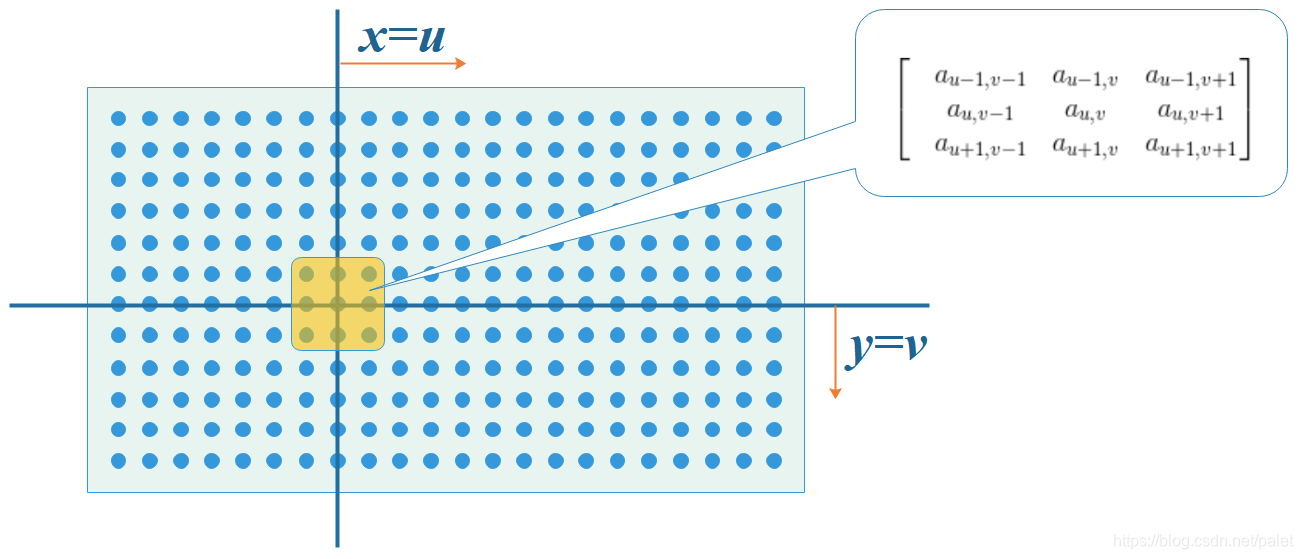
首先我们在原始图像矩阵中取出(u,v)处的矩阵:
接着,需要将图像处理矩阵进行反转,这个反转方式有多种解释,但实际作用相同,包含以下几种操作:(1)先水平颠倒,再垂直颠倒;(2)先水平颠倒,再垂直颠倒,具体操作如下:
原始矩阵:
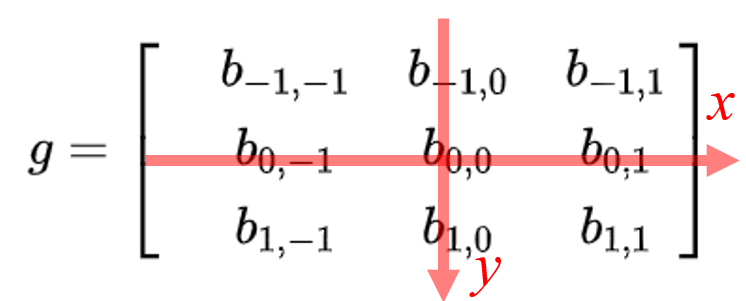
翻转后的矩阵:
(1)先沿x轴翻转开yun体育app入口登录,再沿y轴翻转
矩阵第一行从左到右依次是b_{1,-1}、b_{1,0}、b_{1,1},第二行从左到右依次是b_{0,-1}、b_{0,0}、b_{0,1},第三行从左到右依次是b_{-1,-1}、b_{-1,0}、b_{-1,1},转换后矩阵第一行从左到右依次是b_{1,1}、b_{1,0}、b_{1,-1},第二行从左到右依次是b_{0,1}、b_{0,0}、b_{0,-1},第三行从左到右依次是b_{-1,1}、b_{-1,0}、b_{-1,-1},最终结果等于g的转置形式
(2)先沿y轴翻转,再沿x轴翻转
矩阵先变为另个样子,接着又变回最初形态,等于g的变种形式
计算卷积时,就可以用
的内积:
这个公式有个特性,参与相乘的变量a和b的下标总和恒等于(u,v),这样做是为了对加权累加施加限制。这也是为什么要把矩阵g进行颠倒的原因。
这个计算得出的是在点u和v位置的卷积值,沿着x轴方向或者y轴方向移动,能够计算出图像所有点的卷积,其最终得到的是经过多种处理后的图像,例如包含了平滑和边缘提取等效果。
再仔细琢磨一下,在计算图像卷积时,我们直接从原始图像矩阵中选取了点(u,v)的元素,为什么要选这个位置的元素,根本原因在于需要符合前述的条件。计算(u,v)点的卷积,由于g矩阵为3x3结构,其下标与(u,v)相加必须等于3x3的乘积,因此只能选取原始图像中以(u开元ky888棋牌官网版,v)为基准点的3x3块,也就是图中被标记出来的部分。
换个角度来看,假如g矩阵的规模不是3x3,而是变成了6x6,那么我们就要在原始图像里选取以(u,v)为基准点的6x6矩阵来执行运算。从这里可以看出,这种卷积运算实际上是将原始图像中邻近的像素点全部纳入考量,进而完成合并处理。邻近区域的大小跟g矩阵的尺寸直接相关,尺寸越大,牵涉到的周边像素数量就越多。矩阵的构造方式开yunapp体育官网入口下载手机版,决定了混合生成的画面,与原本的影像相比,是变得不够清晰,还是更加鲜明。
例如,该图像处理矩阵通过合并邻近像素的数值,实施算术平均运算,从而让画面轮廓变得柔和,视觉上呈现出朦胧感:
这种图像处理矩阵能够突出像素值差异显著的区域,增强轮廓线,对于数值变动柔和的部分则不受干扰,最终实现轮廓提取的目标:
对网上一些解释的不同意见
网络上有若干种对卷积的直观说明,比如在知乎问答卷积为何称作「卷」积?中荆哲的见解,以及在问题怎样用浅显易懂的方式解释卷积?中马同学等人的论述里,提出了以下类比。




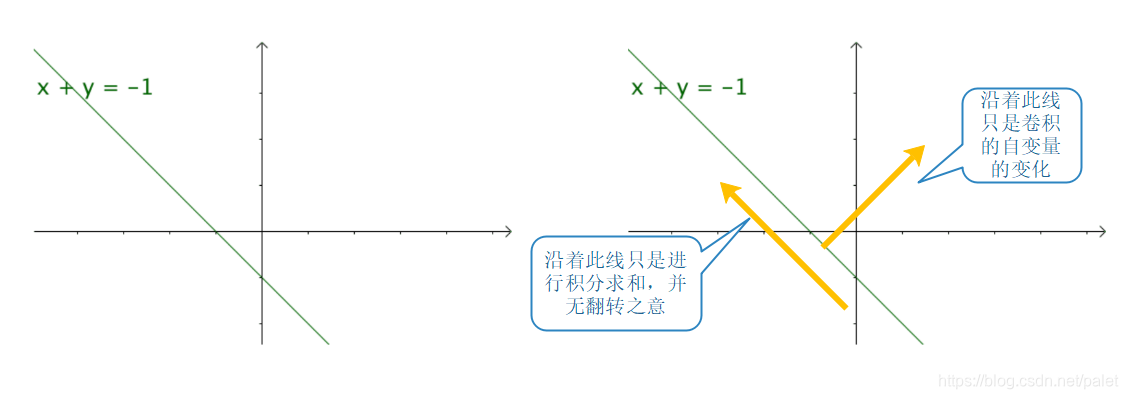
实际上图中所谓的“卷”,指的是进行累加运算的方向,并非表示反转。所以这种说法,并没有把卷积的真正意义讲清楚,对于“卷”的看法需要重新审视。
一些参考资料
《数字信号处理(第二版)》程乾生,北京大学出版社
《信号与系统引论》 郑君里,应启珩,杨为理,高等教育出版社



