pg下载 卷积的通俗解释
原处地址是:《对卷积的困惑》,此知乎里的回答针对卷积给出了截至目前我觉得最为明晰的阐释,现从其中摘取一些内容录下来当作学习笔记,以下全是摘录内容。
文章主要想解释两个问题:
卷积这一专业术语究竟该作出怎样的解说?“卷”所蕴含的是什么释义?“积”所代表的意义又是什么?
2. 卷积背后的意义是什么,该如何解释?
对于卷积这个名词的理解便是pg下载官方版打开即玩v1022.速装上线体验.中国,所谓的两个函数的卷积,其本质实际上就是,先把一个函数进行翻转,之后再进行滑动叠加。
以连续情形而言,叠加所指的是,针对两个函数的乘积去进行求积分,在离散情形时,所为的是加权求和,鉴于要追求简单起见,故而将其统一称作叠加。
整体看来是这么个过程:
多次滑动得到的一系列叠加值,构成了卷积函数。
卷积里的“卷”,是指函数的翻转,即从g(t)变为g(-t)的这个过程,并且,“卷”还有滑动的意思在其中。
卷积的“积”,指的是积分/加权求和。
对卷积的意义的理解:
从“积”的过程来看,我们所获取的叠加值,属于全局概念。以信号分析作例子,卷积结果不仅同当前时刻输入信号的响应值相关,还跟过去所有时刻输入信号的响应都存在关系,考量了对过去所有输入效果的累积。在图像处理里,卷积处理的结果,实际上就是把每个像素周边的,乃至整个图像的像素都纳入考量,用以对当前像素开展某种加权处理。故而讲,“积”属于全局范畴,抑或是一种“融合”,将两个函数于时间或者空间方面予以融合。
那为何要实施“卷”这一操作呢?径直相乘行不通吗?依我所想,开展“卷”(也就是翻转)这一行为,本质目的实则是去施加一种限定,它明确规定了在进行“积”的操作之际,是以什么作为参照标准的。于信号分析的情境当中,它明确规定了是在哪个特定的时间时刻点的前后去开展“积”的操作,在空间分析的情境里,它明确规定了是在哪个位置的周边去开展累积式的处理操作的。
举例说明
下面举几个例子说明为什么要翻转,以及叠加求和的意义。
例1:信号分析
如图所示,输入信号为 f(t),其随时间变动,系统响应函数是 g(t),在此图中的该响应函数随时间呈指数式下降,它的物理意义表明,要是在 t = 0 的时刻存在一个输入,那么随着时间持续流逝,此输入会持续衰减。也就是说,到了 t = T 时刻,原本在 t = 0 时刻的输入 f(0) 的值会衰减成为 f(0)g(T)。
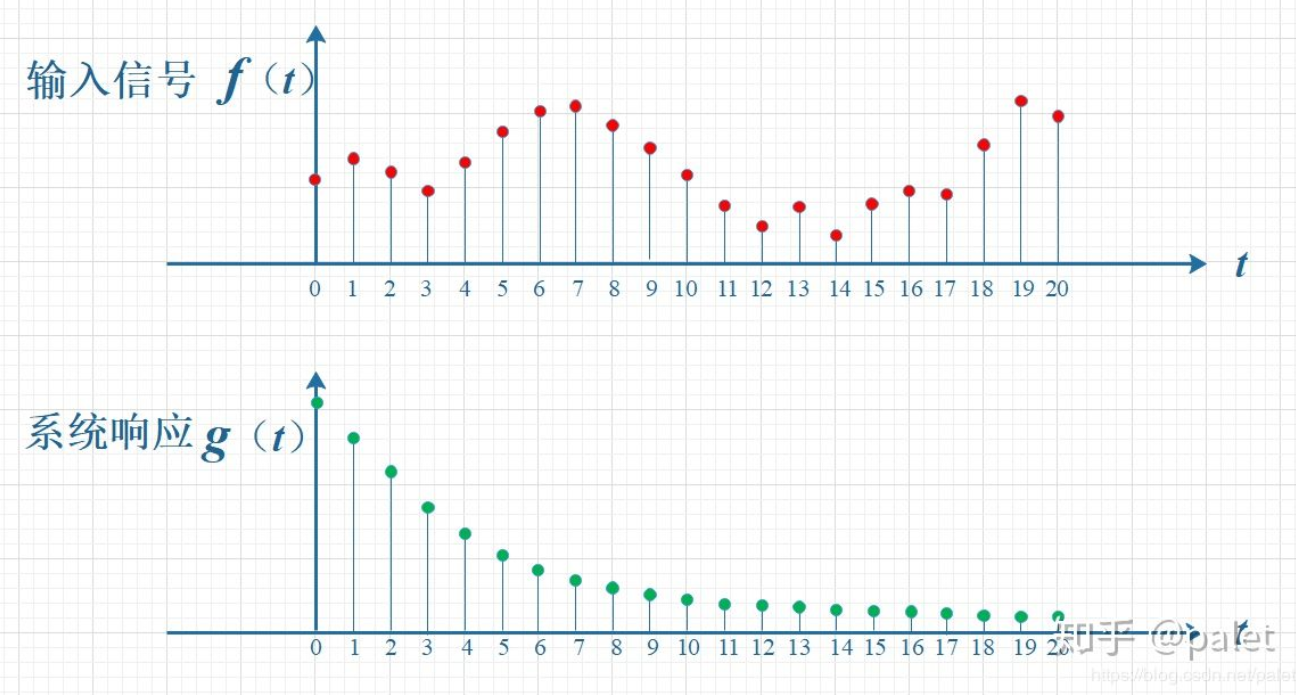
鉴于信号是以连续的方式进行输入,这意味着,在每一个时刻,都会有新的信号进入,所以说来,最终输出的乃是所有之前输入信号的累积成效。如同以下图示所呈现的,在T等于10的时刻,输出的结果与图中带有标记的区域全紧密相关。其中,由于f(10)是刚刚输入的,因而其输出的结果应当是f(10)g(0),而在时刻t为9时输入的f(9),仅仅经过了1个时间单位的衰减,所以所产生的输出应当是f(9)g(1),依此类推,也就是图中虚线所描述的那种关系。把这些对应点进行相乘的操作,之后实现累加这一步骤,所得到的那个值,就是当T等于10这个时刻时的输出信号的值,另外这个值也恰是f与g这两个函数在处于T等于10这个时刻时所产生的卷积的值。
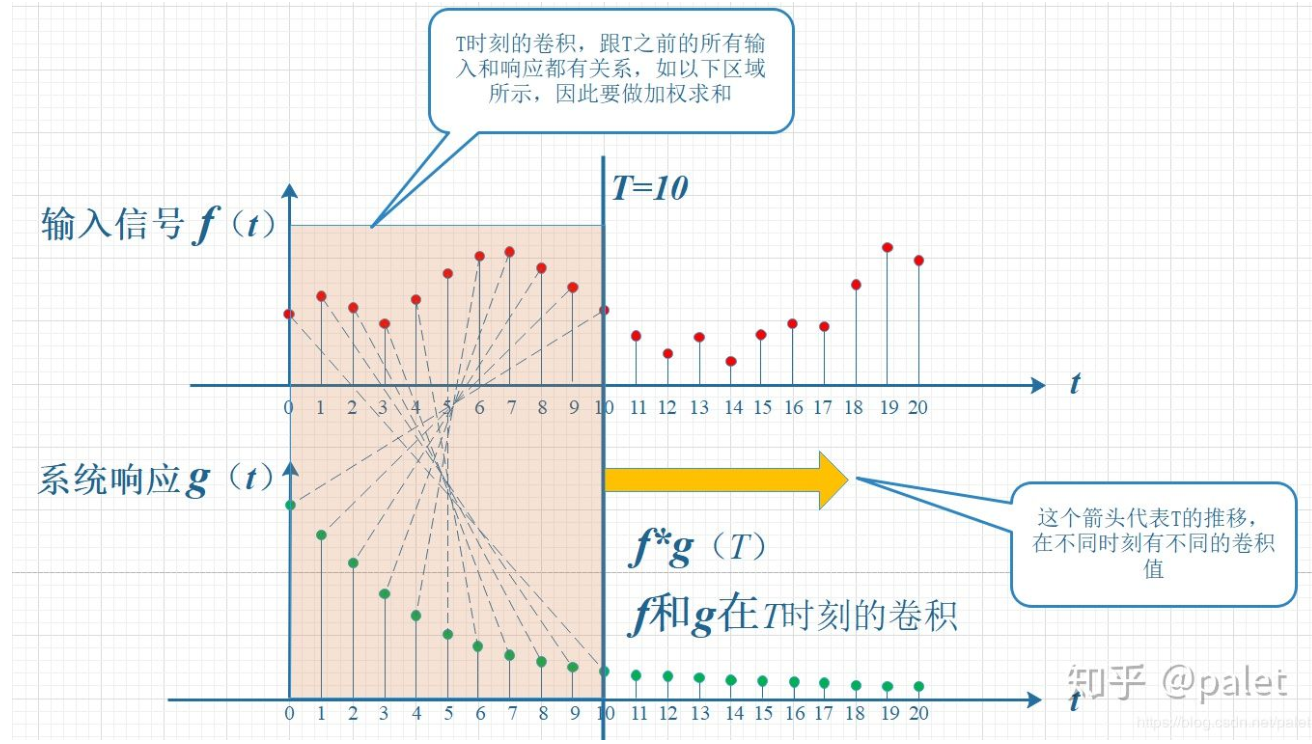
显见,上面所呈现的对应关系看起来较为有碍观瞻,呈现出拧扭的状态,故而,我们将g函数进行对折操作,使之转变为g(-t),如此一来便显得稍好看一点了。瞧见了没?这便是卷积有着“卷”的操作,需要进行翻转的缘由所在。
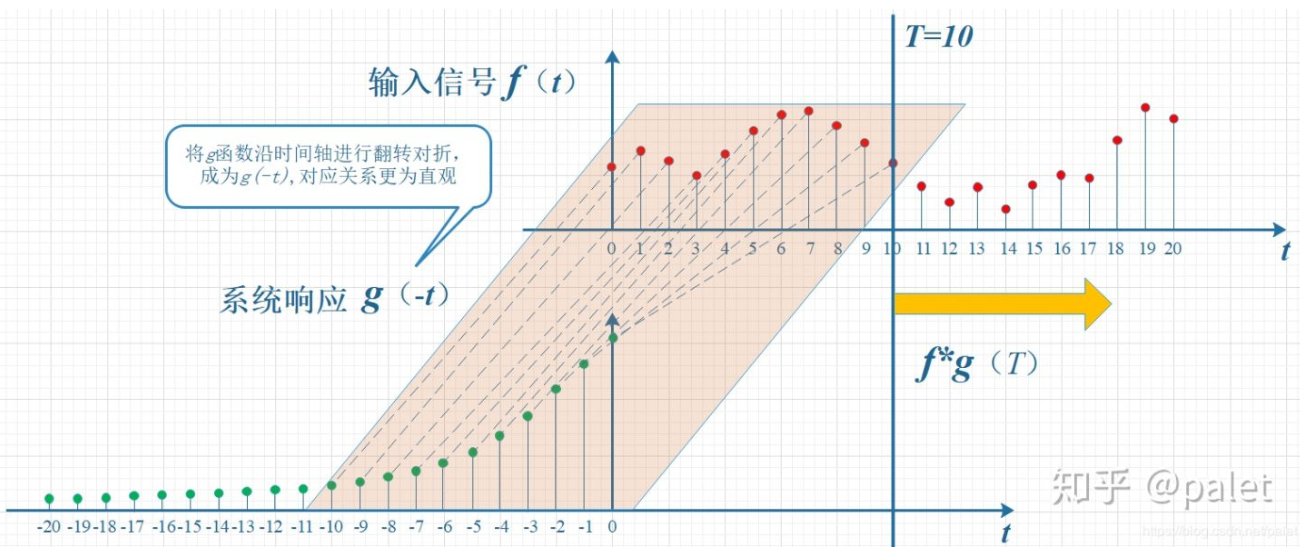
虽未拧着,已然顺过来了,然而看上去仍有少许错位,故而需再进一步平移T个单位,如此便成了下图。它乃是本文起始所给出的卷积定义的一种图形化表述:
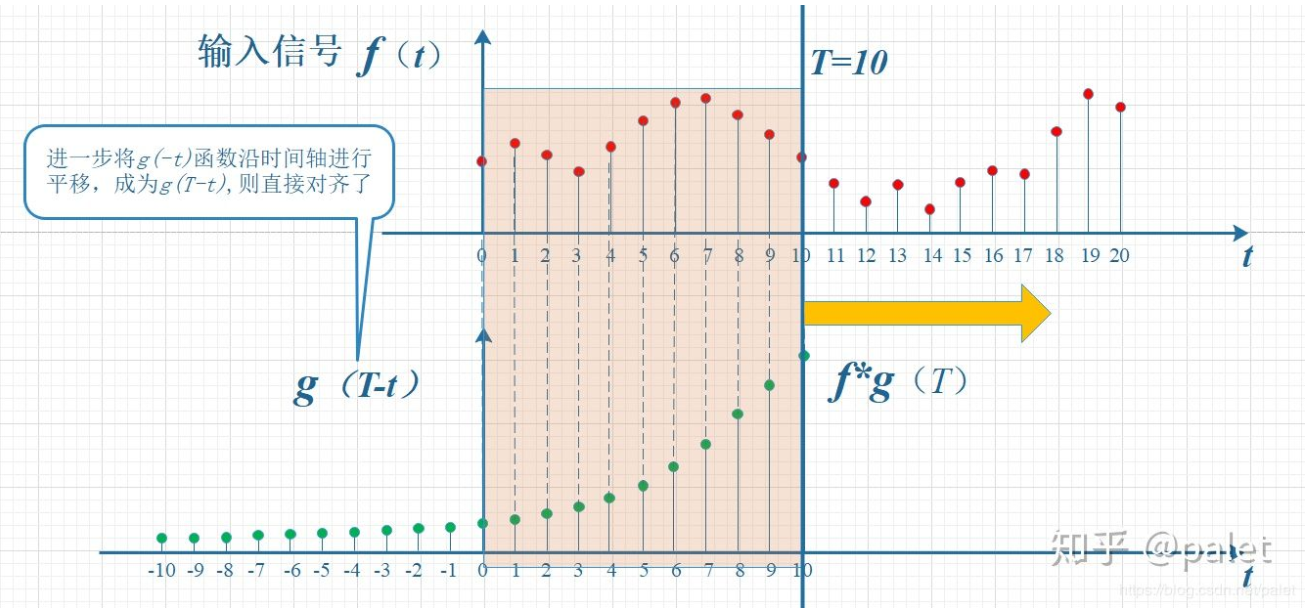
将T时刻的卷积进行计算之时,所要保持的该约束情况便是这般:t加上(T减去t)的结果等于T。
丢骰子
有两个骰子,将它们都扔出去,这两个骰子点数加起来成为4的概率是多少呢?

剖析一下,存在着这样的状况,即两枚骰子所显示的点数二者相加的结果为4,而这种情形具备三种情况,其一乃是1加上3会等于4,其二是2加上2等于4,其三则是3加上1等于4。
因此,两枚骰子点数加起来为4的概率为:
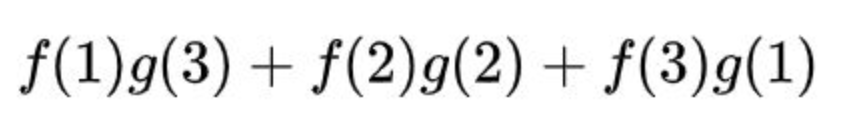
写成卷积的方式就是:
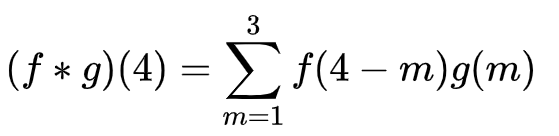
进一步用上面的翻转滑动叠加的逻辑进行解释。
首先,鉴于两个骰子的点数之和是4,为了达成这个约束状况,我们依旧将函数g进行翻转,接着把阴影区域上下所对应的数相乘,随后予以累加,相当于求取自变量是4的卷积值,如下方图示:
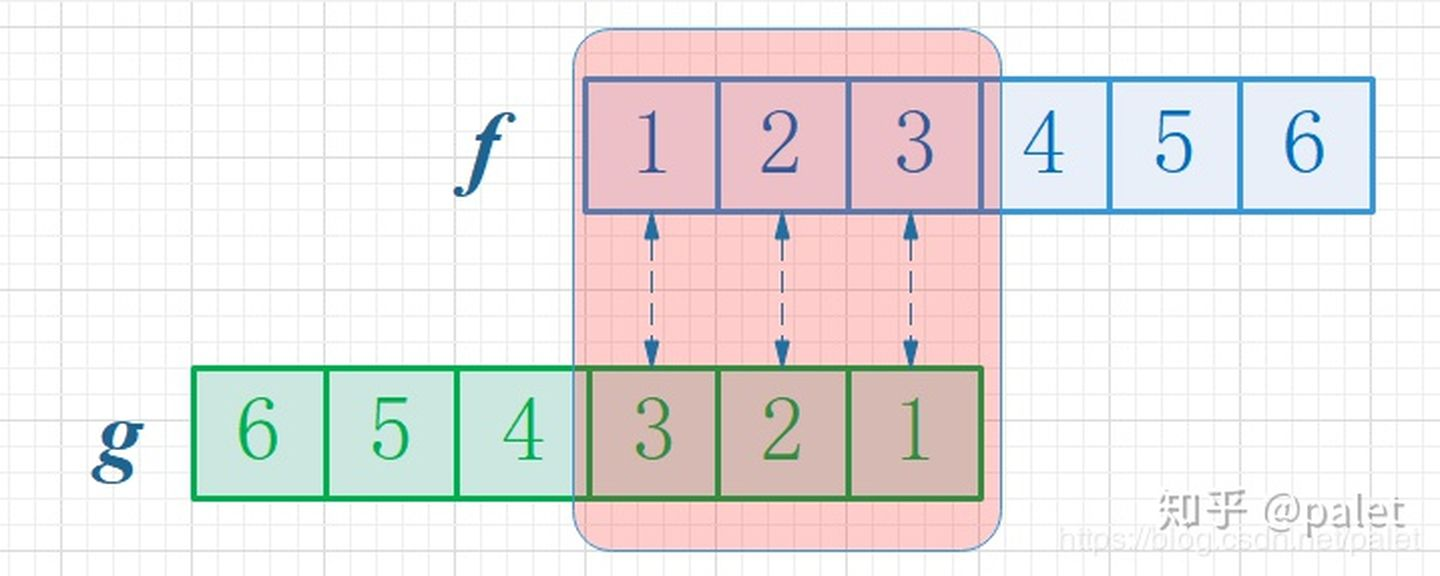
更进一步,这般翻转之后,能够便利地开展推广以去求取两个骰子点数之和为n时的概率,此概率为f与g的卷积f*g(n),呈现如下图示标点符号:
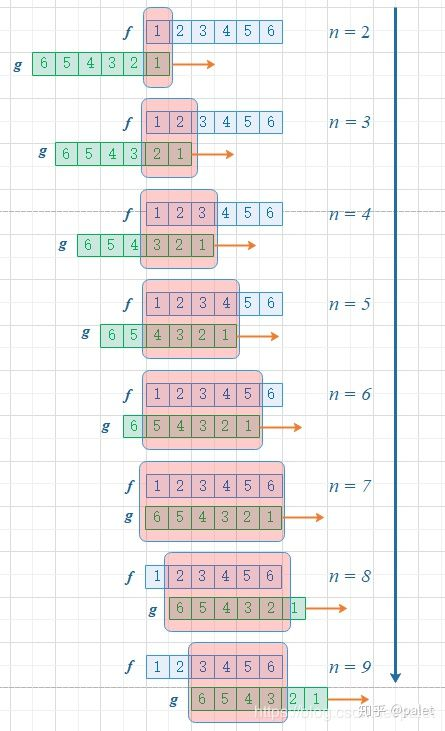
从上面那张图能够瞧见,函数g发生滑动这件事,所造成的结果是点数和呈现出增大的态势。在这个具体的例子当中,针对f以及g而言的约束内容就是点数和,它同样也是卷积函数里处于自变量地位的那个量。要是你有这样的兴致,还能够进行一番推算,要是骰子的每一个点数现身的概率都是一样的,那么当两个骰子的点数和n等于7这个情况出现的时候,概率是最大的。
图像处理
图像可以表示为矩阵形式:
对于图像的处理函数,像是平滑处理函数,或者边缘提取处理函数,同样能够借助一个g矩阵予以表示,情况如下:

仅从卷积的定义去看,应当是向着x跟y这两个方向展开累加计算(这与上面离散公式里的i、j这两个下标相对应),并且这种累加是没有界限限制的,从负无穷一直延伸至正无穷。然而,现实当中的世界全部都是存在界限的。比如说,上面所列举出来的图像处理函数g实际上就是一个3乘3的矩阵,这便意味着,在除去原点附近的区域以外,其他所有点的取值都是0。当综合考量这个因素之后,上面提及的公式实际上出现了退化的情况,只将坐标(u,v)附近的那些点挑选出来进行计算了。所以,实际的计算呈现如下:
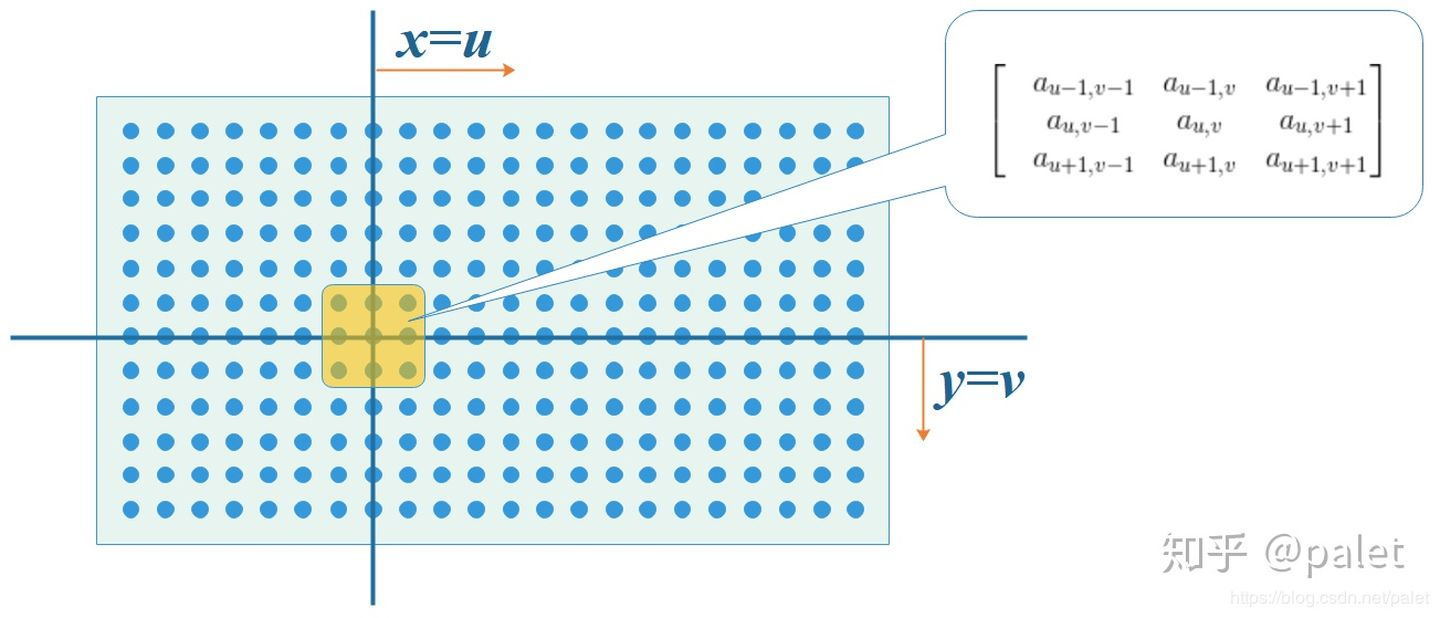
首先我们在原始图像矩阵中取出(u,v)处的矩阵:
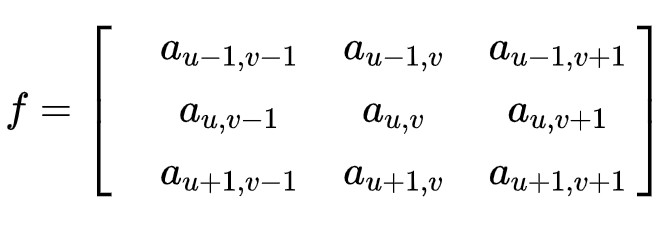
接着把图像处理矩阵进行翻转,(此翻转颇具意味,能够存在几种不一样的理解,其成效是等同的:(1)先是沿着x轴施行翻转,随后沿着y轴予以翻转;(2)先是沿着x轴进行翻转,之后沿着y轴加以翻转),情况如下:
原始矩阵:
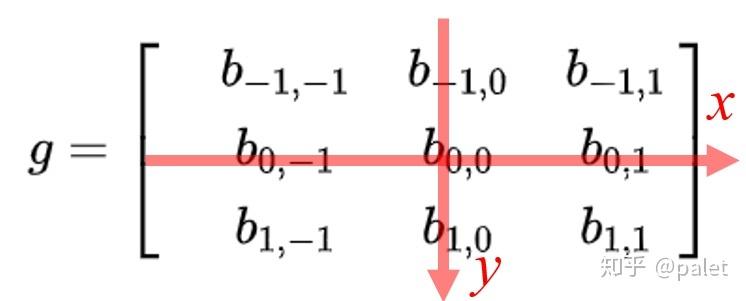
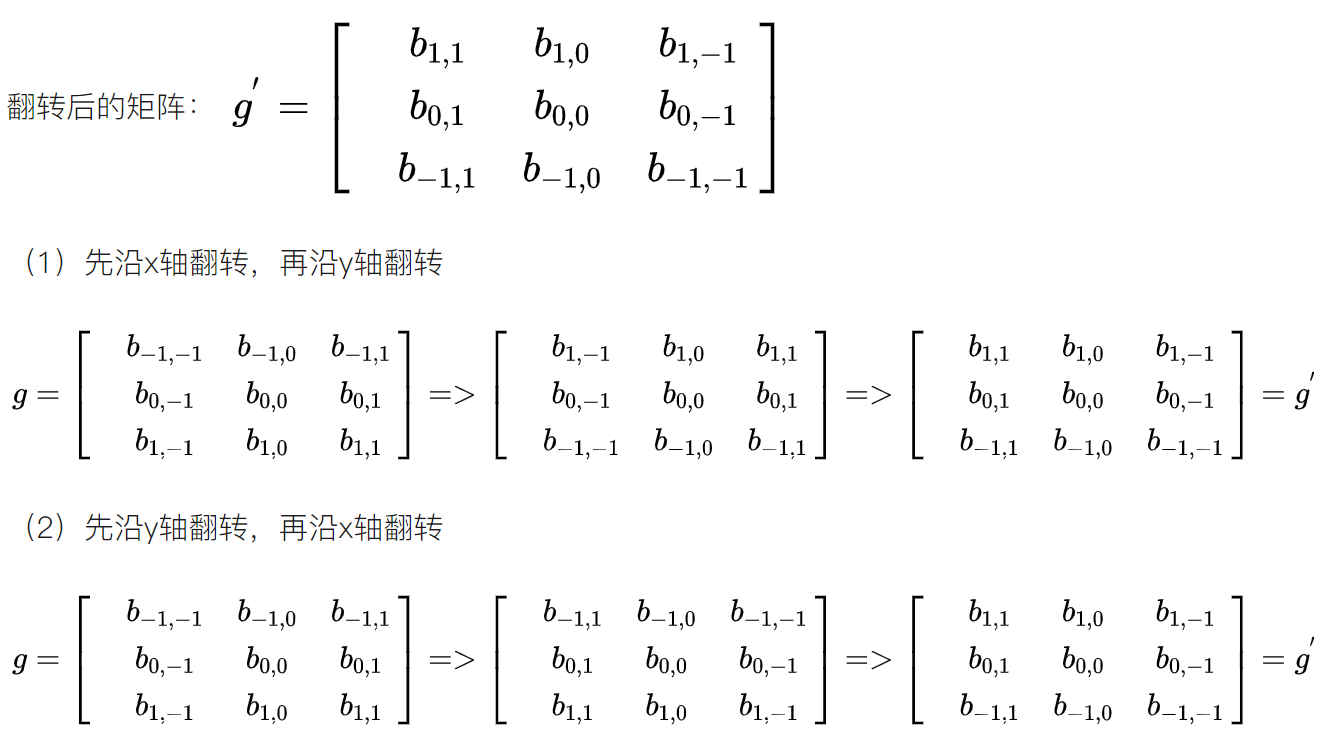

请注意,以上公式具备一个特点是,做乘法之中的两个对应变量a与b的下标之和全都是(u,v),其目的在于对这种加权求和予以一种约束,这也是要将矩阵g进行翻转的缘由,以上矩阵下标之所以如此书写并且进行了翻转,是为了能让大家更清晰地看到与卷积的关系,这样做的益处是便于推广,还便于理解其物理意义,实际在计算之际,都是采用翻转以后的矩阵,直接求矩阵内积便行了。
以上所进行计算的,是处于(u,v)那个位置的卷积pg下载渠道,沿着x轴或者y轴进行滑动处理,如此便能够求出图像当中各个位置的卷积,其最终的输出结果就是经过了处理之后的图像,也就是那种经历过诸如平滑、边缘提取等各种各样处理的图像。
在进行图像卷积计算之时是直接于原始图像矩阵当中选取了处于(u,v)位置的矩阵,为何要选取该位置的矩阵呢,从本质上来说实际上依旧是意图满足上述的约束条件。
我们要算(u,v)处的卷积,g矩阵是3x3的矩阵,要满足下标与这个3x3矩阵(就是g矩阵)之和为(u,v),那就只能取原始图像中以(u,v)为中心的那个3x3矩阵,也就是图中阴影区域的矩阵。
继续延伸下去进行更广泛的推导,要是g矩阵并非3x3,而是变成7x7,那么我们就得在原始图像那里选取以(u,v)作为中心的7x7矩阵来开展计算。从这里能够明显看出,这样的卷积就是把原始图像里相邻的像素全部纳入考量范围,从而进行混合操作。相邻的区域范围是由g矩阵的维度所决定的,只要维度越大,所涉及到的周边像素数量就会越多。
g矩阵所进行的设计,有着这样的作用,它能够决定,是这种混合输出的图像相较于原始图像而言,出现了影像不再清晰存在模糊情况,还是图像变得更加清晰锐利了。
假设存在这样一种情况,如同这样一种图像处理矩阵,它会致使图像产生变化,这种变化就是让图像变得更为光滑顺畅,呈现出一种更为模糊的状态,其原因在于它结合了周边相邻的像素实施了平均化的处理操作:
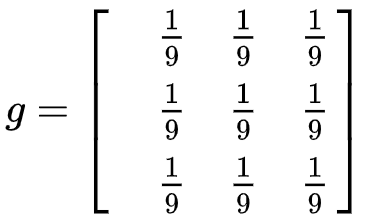
有这样一种图像处理矩阵,它会让像素值变化显著之处变得更加突出,以此来强化边缘,并且对于像素值变化平缓的地方没有产生任何影响,最终达成提取边缘的目标,具体如下:
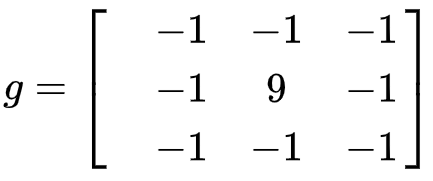
对一些解释的不同意见
知乎问题卷积为什么叫「卷」积?中 荆哲 提出如下比喻:
荆哲
看起来好似将一张呈现二维形态的地毯,从角落沿着与水平方向成45度夹角的斜线进行卷曲,我对于此的理解便是如此。
补充:
这儿有一张地毯,它是正方形的,其上留存着f跟g于区间的张量积,也就是U(x,y)等于 f(x)g(y)。

我把它一角卷起来。

好了,把它整张地毯卷起来以后,

能够看得出来pg下载麻将胡了安卓专属特惠.安卓应用版本.中国,其转变成为了一个属于一维的函数,并且呢,每一个点的函数数值等于卷起来之后相互重合的那些点的函数数值的总和。
现在把地毯展开。

能够看得出,适才被画上道道的所在之处,恰好就是横坐标与纵坐标之和为固定数值的一条直线,因而卷起来之后那一点的函数数值正好是这条直线上函数数值的积分。如何,是不是特别形象?


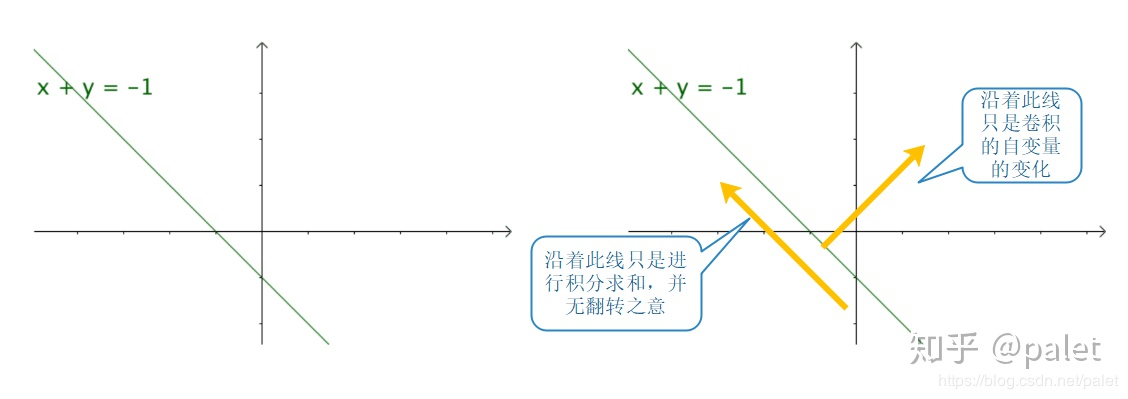
其中,图里“卷”的方向,乃是顺着该方向开展积分求和的方向,不存在翻转的意思。所以,这般解释,并未完整表述出卷积的含义,对于“卷”的理解是值得去探讨一番的。