pg下载通道 一文读懂 12种卷积方法

来源:机器之心 本文约7800字,建议阅读15分钟
本文归纳总结深度学习中常用的几种卷积,并会试图用一种每个人都能理解的方式解释它们。
我们全都清楚卷积的重要意义程度,然而你可晓得深度学习范畴里面的卷积到底究竟为何物,并且存在着多少种类别吗,研究学者 Kunlun Bai最近时候发布了一篇讲述介绍深度学习的卷积的文章,以易于理解明白的方式介绍了深度学习领域范围之内之中的各种各样类型的卷积以及它们存在拥有的优势长处,由于鉴于原文篇幅过长,机器之心挑选选取了当中部分内容开展介绍讲述,2、4、5、9、11、12节请查看参阅原文。
倘若你听闻过深度学习里不同类别的卷积,像2D卷积、3D卷积、1x1卷积、转置卷积、扩张(Atrous)卷积、空间可分卷积、深度可分卷积、平展卷积、分组卷积、混洗分组卷积,而且弄不明白它们到底是什么含义,那么这篇文章便是为你所撰写的,能够助你领会它们实际的工作模式。
关于这篇文章,我要去把深度学习里常常会被运用的那些不一样的卷积进行归纳梳理概括起来,而后尝试着借助一种能够让每一个人都可以把握弄懂进而领会明白的方式去把它们作出解释。
期盼着当下这篇文章,能够助力你去搭建起对于卷积的那直观的认知,并且还能成为你在开展研究或者进行学习时的具备有用性的参考。
本文目录
1. 卷积与互相关
2. 深度学习中的卷积(单通道版本,多通道版本)
3. 3D 卷积
4. 1×1 卷积
5. 卷积算术
6. 转置卷积(去卷积、棋盘效应)
7. 扩张卷积
8. 可分卷积(空间可分卷积,深度可分卷积)
9. 平展卷积
10. 分组卷积
11. 混洗分组卷积
12. 逐点分组卷积
一、卷积与互相关
在信号处理范畴,图像处理范畴,以及其它工程或者科学领域范围之内,卷积是一项应用idespread并且广泛的技术。于深度深度学习领域当中,卷积神经网络也就是那个被称为CNN的模型框架架构,它是由于这种该技术而闻名获名以此得来名称的。然而可是,深度学习领域范畴里的卷积,从本质上来说实质上是信号又或者图像处理领域范围内部的cross-correlation这个互相關。而这此两者这两种操作之间,却存在着一些细微不太明显的差别。
不必要过分深入到细节当中,我们便能够看见这个差别,在信号以及图像处理的领域范围之内,卷积的定义是这样的。
其定义为,一个函数在经过反转操作后,再进行位移操作,之后与另一个函数相乘,所得到的积,对这个积进行积分。下面的可视化呈现了这一理念:
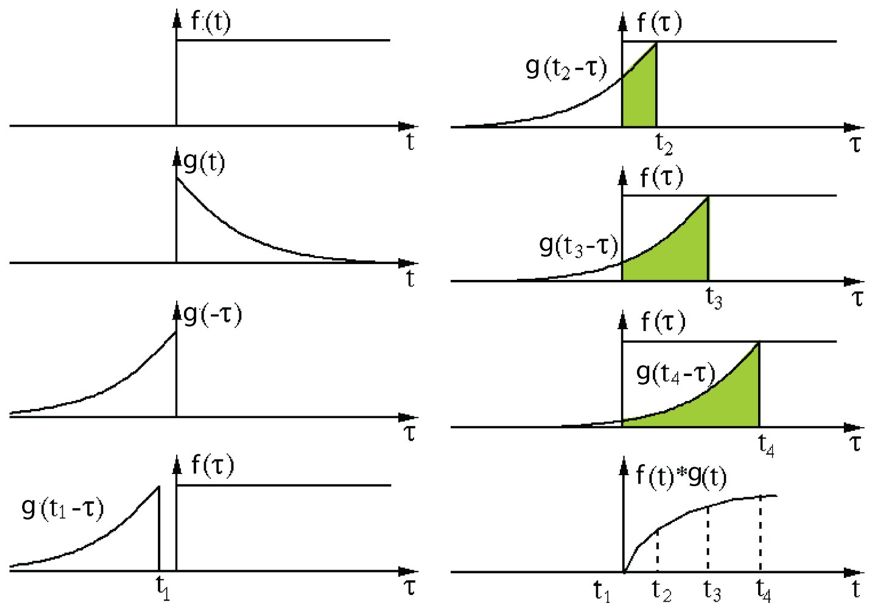
信号处理里的卷积,过滤器g被反转,之后沿着水平轴滑动,在每个位置,我们计算f与反转后的g之间相交区域的面积,这个相交区域的面积是特定位置的卷积值。
在这里,函数 g 身为过滤器,它经过反转操作后,接着沿水平轴进行滑动,在每一个位置上,我们都会去计算 f 与反转后的 g 之间相交区域的面积,而这个相交区域的面积便是特定位置处的卷积值。
再说另一方面,互相关乃是那两个函数之间进行着的、滑动着的点积或者那滑动着的内积。互相关里头存在的过滤器并非要经过反转这一步后再进行,而是直接就这么滑过函数 f。函数 f与函数 g之间所形成穿插相连的部分区域就是互相关。紧跟在这里的这张图呈现出了卷积同那个互相关之间存在着的差异。
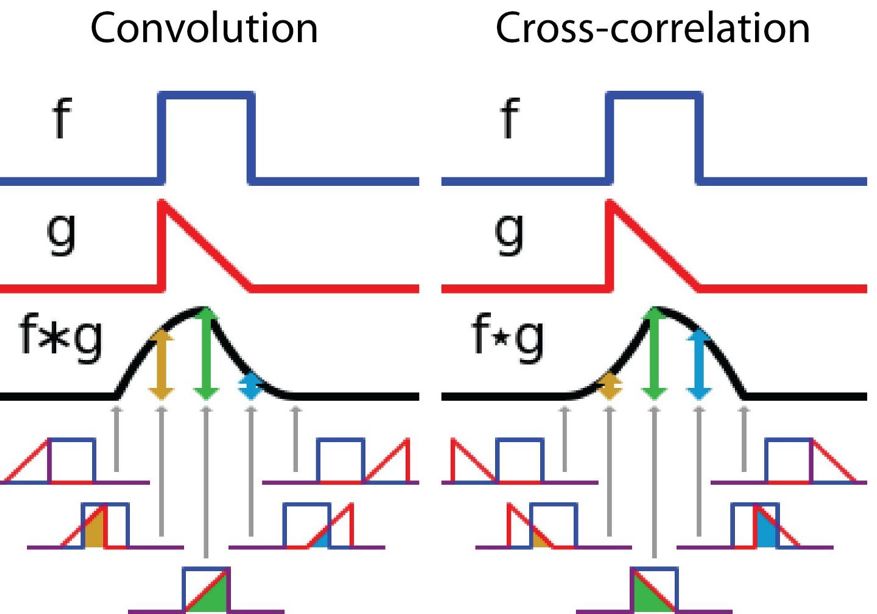
信号处理中卷积与互相关之间的差异
在深度学习里头,卷积当中的过滤器是不进行反转操作的。确切来讲,这实际上是互相关。我们从本质上来看,是在执行逐元素的乘法以及加法。然而在深度学习里,直接把它称作卷积会更为便利。这是没有什么问题的,原因在于过滤器的权重是在训练阶段被学习到的。要是上面例子里的反转函数g属于正确的函数,那么在经过训练之后,学习所得到的过滤器看上去就会如同是反转后的函数g。所以,在训练之前,并不需要像在真正的卷积当中那样先去反转过滤器。
二、3D 卷积
在前面那一节的阐释当中,我们发现我们事实上所做的是针对一个三维体积展开卷积操作,然而,一般情况下,在深度学习领域我们依旧将其称作二维卷积,这可是施加于三维体积数据之上的二维卷积,该过滤器的深度跟输入层的深度相同哩,这个三维过滤器仅仅沿着两个方向进行移动 ,也就是图像的高度方向以及宽度方向,而这种操作最终所产生出来的结果是一张二维图像 ,并且这张二维图像只有一个通道。
蛮自然的,3D卷积的确是存在着的 ,它属于2D卷积的一种泛化情形。接下来呈现的便是3D卷积 ,其过滤器的深度要比输入层深度小(核大小>m) ,于是这个比值也就变成了2/m。换句话讲 ,在这种渐进情况之下(N>>m) ,当过滤器的大小是3×3时 ,空间可分卷积的计算成本为标准卷积的2/3。而当过滤器大小是5×5时 ,此数值是2/5。当过滤器大小为7×7时 ,该数值则是2/7。 句号。
纵使空间可分卷积具备削减成本之能力,然而深度学习对其运用却颇为稀少。其中一关键缘由在于,并非全部核均可拆解为两个体量更小之核。倘若我们借由空间可分卷积替换所有传统卷积,那么我们便会在训练进程中束缚自身去探寻所有潜在之核。如此一来所获取的训练效果或许是处于次优状态的。
2、深度可分卷积
现阶段来观察思考深度可分卷积,那在深度学习该范畴的通常使用频率可要高得多了(像 MobileNet 和 Xception 这样子的情况)。并且深度可分卷积是有包涵两个步骤的:其一为深度卷积,另一则是核 1×1 卷积。
在对这些步骤予以描述之前,有进行回头看一下我们先前介绍的2D卷积核1×1、卷积的必要。首先,对标准的2D卷积进行快速的回顾。列举一个具体的例子,假定(假设)输入层在大小方面是7乘7乘3(高乘以宽乘以通道),然而过滤器的大小是3乘3乘3。在经历与一个过滤器所进行的2D卷积之后,输出层的大小是5乘5乘1 (仅仅有一个通道)。
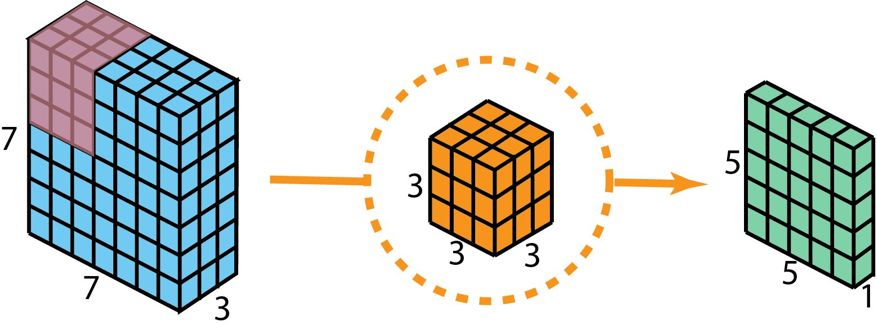
打造仅具备分层为一输出状况所需运用的既定二维卷积方案 且借助单个过滤器实现。
通常来讲,于两个神经网络层的中间部分,会运用多个过滤器,假定此刻我们有一百二十八个过滤器,在执行了这一百二十八个二维卷积之后,我们得到一百二十八个五乘五乘一的输出映射,之后我们将这些映射堆积成尺寸为五乘五乘一百二十八的单个层,借由这种操作,我们能够把输入层也就是七乘七乘三变换成输出层五乘五乘一百二十八,空间的维度也就是高度与宽度会变小,然而深度会加大。
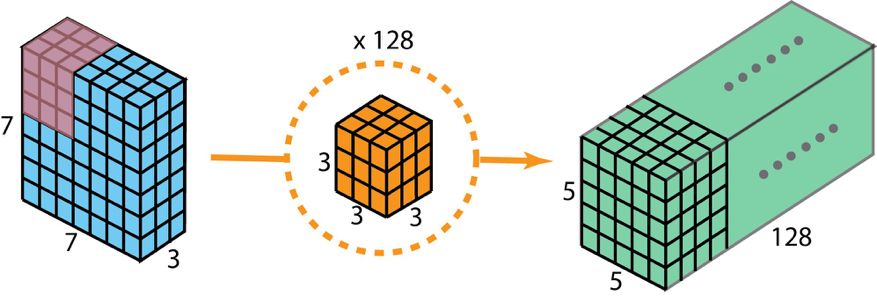
用于创建输出的标准 2D 卷积,该输出有 128 层,要使用 128 个过滤器。
现在使用深度可分卷积,看看我们如何实现同样的变换。
起初,我们把深度卷积运用在输入层。然而我们并非选用 2D 卷积里那种大小是 3×3×3 的单一过滤器,而是分别采用 3 个核。每个过滤器的尺寸为 3× 3×1。且每个核跟输入层的一个通道进行卷积(仅仅是一个通道,并非所有通道)。每一次这般的卷积均可给出大小为 5×5×1,的映射图。随后我们把这些映射图堆积到一起,构建出一个 5×5×3 的图像。在历经这个操作后,我们取得大小为 5×5×3 的输出。现在我们可以降低空间维度了,但深度还是和之前一样。
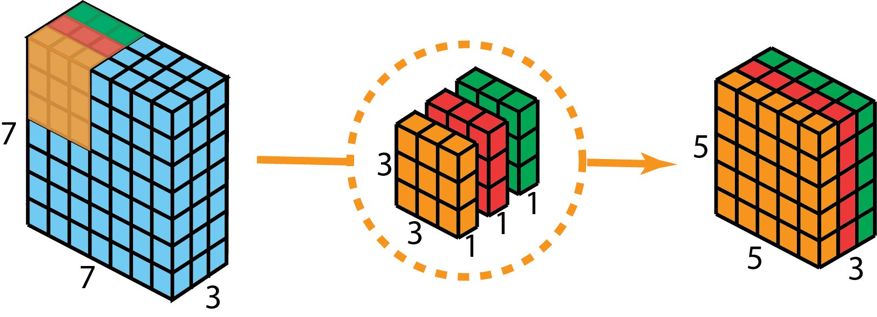
深度可分卷积,第一步:不是采用 2D 卷积里大小为 3×3×3 的单个过滤器,而是把仅一个通道与输入层卷积的 3 个大小为 3×3×1 的核分开来使用,这样每个核与之卷积后能提供大小为 5×5×1 的映射图,接着把这些映射图堆叠在一起从而创建出一个 5×5×3 的图像,经过此操作后便得到大小为 5×5×3 的输出。
进行深度可分卷积的第二步时,为了把深度进行扩展,我们运用一个核体大小为1×1×3的1×1卷积操作。采用使5×5×3的输入图像同每个1×1×3的核去卷积,能够获取到大小为5×5×1的映射图形。
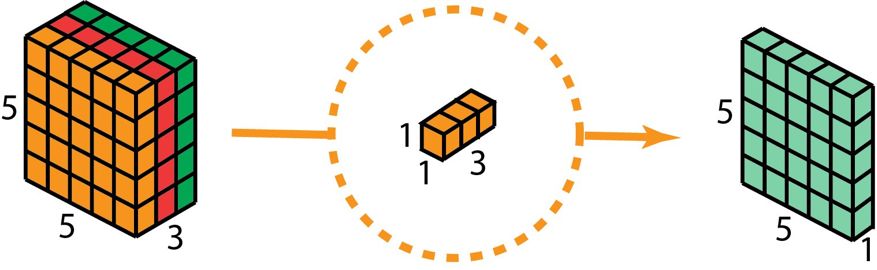
为此,于运用了 128 个 1×1 卷积之后,予以获取为大小 5×5×128 的层。
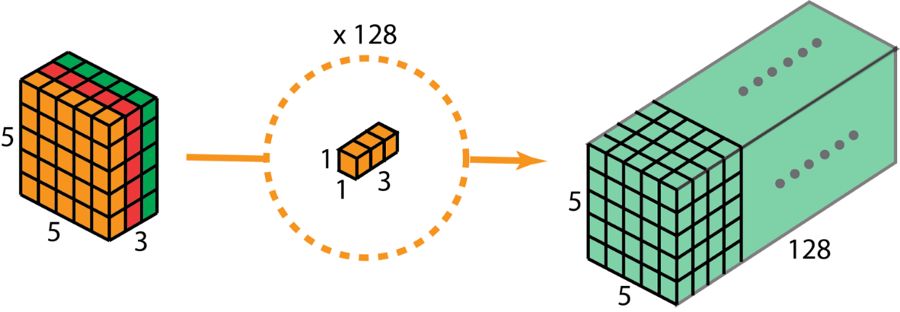
深度可分卷积——第二步:应用多个 1×1 卷积来修改深度。
经过这两个步骤,深度可分卷积同样会把输入层:(7×7×3),转变为输出层:(5×5×128)。
下图展示了深度可分卷积的整个过程。
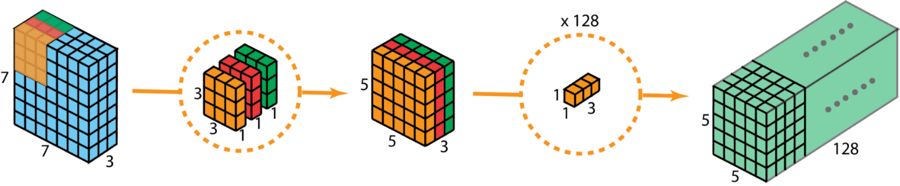
深度可分卷积的整个过程
因此,深度可分卷积究竟具备怎样的优势咧?是效率!相较于2D卷积而言,深度可分卷积所需要的操作要少上许多。
回顾一下,我们那个,涉及到2维卷积例子的,进行运算时候的所耗成本。存在着128个这样的核元素,每个的数值规格是3乘以3再乘以3,它经过运算移动的次数是5乘以5次那种情况,也就是,这样计算所出现的,乘法次数是128与3和3和3以及5和5接连相乘所造成下所得出结果为86400次。
那可分卷积究竟怎样呢?第一阶段深度卷积时,存在3个尺寸为3×3×1的核,其移动运算达5×5次,经计算得3x3x3x1x5x5 = 675处乘法运算。于1×1卷积的第二个步骤里,有128个尺寸为1×1×3的核,移动次数是5×5次,也就是128 x 1 x 1 x 3 x 5 x 5 = 9600处相乘操作。所以,深度可分卷积的乘法运算总数为675 + 9600 = 10275次。如此这般的成本大约仅仅是2D卷积成本的12%!
所以,针对任意尺寸的图像而言,一旦我们运用深度可分卷积,我们能够节省多少时长。来,咱们把这些之上的示例啊泛化掉。此刻,对于具备 H×W×D 这般大小的输入图像哟,如果是以 Nc 个有着尺寸为 h×h×D 的核去执行 2D 卷积哒(步幅是 1,填充值为 0嗷,这里面 h 可是偶数哒)。为了要把输入层(H×W×D)给变换成输出层((H - h + 1)x (W - h + 1) x Nc),所需要的总共乘法次数是:
另一方面,对于同样的变换,深度可分卷积所需的乘法次数为:
D乘以h乘以h乘以1乘以(H减h加1)乘以(W减h加1),加上Nc乘以1乘以1乘以D乘以(H减h加1)乘以(W减h加1),等于(h乘以h加上Nc)乘以D乘以(H减h加1)乘以(W减h加1)。
则深度可分卷积与 2D 卷积所需的乘法次数比为:
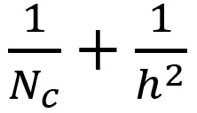
在现代,大多数架构的输出层,常常会有诸多通道,数量能够达到数百,甚至是上千。对于这样的层来讲,条件是通道数量大于高度(Nc >> h),那么上述式子就能够约简成为1 / h²。就基于这个情况而言,要是使用3×3的过滤器,那么2D卷积所需要的乘法次数,是深度可分卷积的9倍。要是使用5×5的过滤器,那么2D卷积所需要的乘法次数,是深度可分卷积的25倍。
深度可分卷积会致使卷积里参数的数量出现降低的状况,这是不是深度可分卷积存在某种坏处呢?答案必定是存在的,正因如此,对于规模较小的模型来讲,要是运用深度可分卷积去替换二维卷积这项2D卷积,那么模型所具备的能力很有可能会产生显著的下降态势,所以基于这般情况所获得的模型极有可能是处于次优范畴的。然而,要是能够做到合理恰当的使用,深度可分卷积会在不致使你的模型性能出现降低的整体前提局面之下,为你达成效率方面的有效提升,以此让你在相关操作过程中获得更好的效果。
六、分组卷积
分组卷积由 AlexNet 论文(https://papers.nips.cc/paper/4824-imagenet-classification-with-deep-convolutional-neural-networks.pdf)于 2012 年所引入。而进行分组卷积的主要缘由在于使得网络训练能够在 2 个内存受限,每个 GPU 仅有 1.5 GB 内存的 GPU 上开展。下面的 AlexNet 显示,在多数层里,存在着两条分离的卷积路径。这是于两个 GPU 上开展模型并行化,当然,要是能够运用更多 GPU,还能够进行多 GPU 并行化。
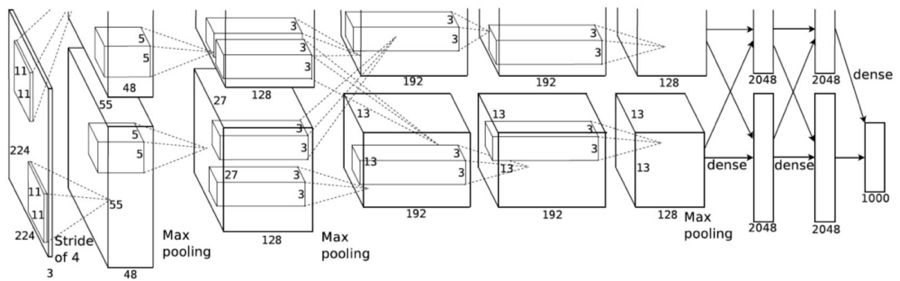
图片来自 AlexNet 论文
这里我们对分组卷积的工作方式予以介绍,首先,典型的2D卷积步骤以如下图形展示,在这个例子当中,凭借应用128个尺寸为3×3×3的过滤器把输入层(7×7×3)转变为输出层(5×5×128)pg下载赏金下载,推广来讲,也就是借助应用Dout个维度为h x w x Din的核将输入层(Hin x Win x Din)转化成输出层(Hout x Wout x Dout)。
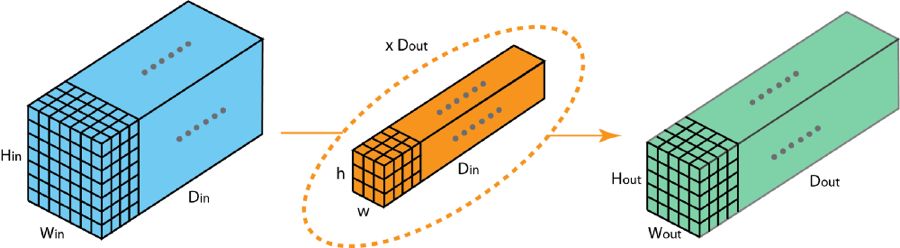
标准的 2D 卷积
于分组卷积里头,过滤器会被划分成不一样的组,每一组都承担着特定深度的典型二维卷积。下面所举的例子能使你更加清晰地领会。
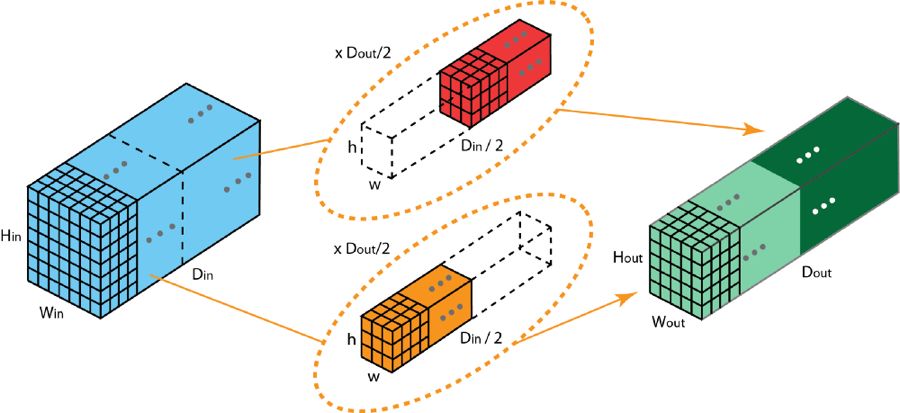
具有两个过滤器分组的分组卷积
具有两个过滤器分组的分组卷积,被上图展示了。在每个过滤器分组里,每个过滤器的深度,仅有名义上的2D卷积的一半儿。它们的深度是Din/2。存在每个过滤器分组,其包含Dout/2个过滤器来着。第一个过滤器分组(红色),和输入层的前一半。
:, :, 0:Din/2
)卷积,而第二个过滤器分组(橙色)与输入层的后一半(
:, :, Din/2:Din
具有卷积情况,所以,每一个过滤器分组就建构起 Dout 除以 2 的这般数量的通道。从整体情形上来瞧pg下载麻将胡了安卓专属特惠.安卓应用版本.中国,两个分组会造就出 2 乘以 Dout 除以 2 等于 Dout 数量的通道。随后,我们把这些通道依照顺序堆叠到一块,最终获取到拥有 Dout 个通道的输出层。
1、分组卷积与深度卷积
你或许会留意到,分组卷积跟深度可分卷积当中所运用的深度卷积之间,存在着一些关联以及差别。要是过滤器分组的数目跟输入层通道的数目相等,那么每个过滤器的深度就是 Din/Din = 1。如此这般,这样的过滤器深度就和深度卷积里的是一样的了。
在另外一方面,当下每一个的过滤器分组当中,都涵盖着Dout/Din个过滤器。从整体的角度来讲,输出层所具有的深度是Dout。这跟深度卷积的情形是不一样的,深度卷积是不会让层的深度产生改变的。在深度可分卷积里,层的深度之后是借助1×1卷积来予以扩展的。
分组卷积有几个优点。
第一个优点在于,具备高效训练 的那般情况。由于卷积被划分成了多个路径,且每个路径能够由不同的 GPU 予以分开处理,致使模型能够以并行的方式,在多个 GPU 上展开训练。相较于在单个 GPU 上完成所有任务这种情形,那般在多个 GPU 上的模型并行化,得以让网络在每一个步骤去处理更多图像。人们通常认定,模型并行化较之于数据并行化更好。而后者是把数据集划分成多个批次,随后分开训练每一批。但是,存在这样一种情况,当真的出现批量的大小变得过小的状况时,我们实际上所执行的便是随机梯度下降,而并非批梯度下降。它会导致这样的后果,会造成进展变得更慢,并且有时候还会出现更差的收敛结果。
在神经网络训练流程已十分深度化时pg下载通道,涉及分组操作的卷积具备了相当重要且关键的地位,此情形可参照已然成为一种典型范例的ResNeXt中的相关情况。
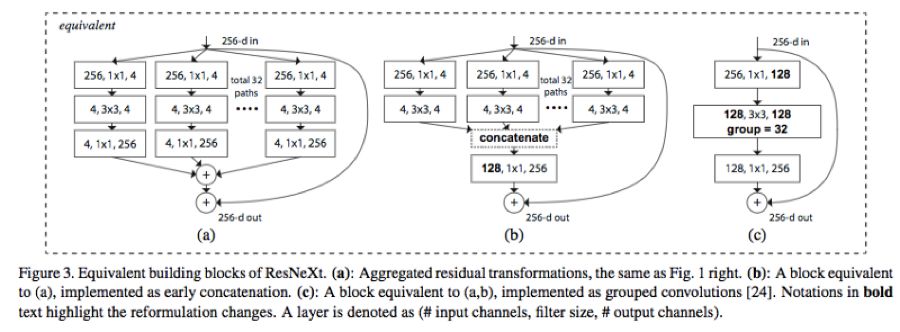
一些图片,它们源自 ResNeXt 这篇论文,其链接为 https://arxiv.org/abs/1611.05431。
第二其优点为模型更具高效性,也就是随着过滤器分组数额增大,模型的诸多参数会有所减少。于先前例子里,完整的标准二维卷积具备h乘以w乘以Din乘以Dout个参数。有着两个过滤器分组的分组卷积情形下,有括号内h乘以w乘以Din除以二乘以Dout除以二再乘以二这么多个参数其数量是减少了一半的。
有些令人诧异的是第三个优点,分组卷积有可能会提供胜过标准完整2D卷积的模型,另一篇优秀的博客对此做出了解释,其链接为:https://blog.yani.io/filter-group-tutorial,在此进行简要的概括。
情况跟稀疏过滤器的关联存在着原因方面的联系,有一张图示呈现的是相邻层次过滤器之间的相关性,当中所具备的那种关联呈现出一种稀疏的特性。

有一个在CIFAR10上进行训练的模型,它是Network - in - Network模型,其中相邻层的过滤器具有相关性矩阵,该矩阵生成的图片里,过滤器相关性高度相关的部分会呈现得更明亮,而相关性更低的部分呈现得更暗,图片源自https://blog.yani.io/filter - group - tutorial。
分组矩阵的相关性映射图又如何?

在一个于CIFAR10上训练而成的Network - in - Network模型里,相邻层过滤器之间的相关性得以呈现出不同特点,有不同数量过滤器分组的情况通过动图分别展示,具体为有1个过滤器分组的情景,、存在2个过滤器分组的情景,4个过滤器分组的情景,8个过滤器分组的情景,以及16个过滤器分组的情景,这些图片源自https://blog.yani.io/filter - group - tutorial 情景,进而得以分别展示对应的情景标点符号。
那篇文章所提推理为,上图呈现的是,当动用1、2、4、8、16个过滤器分层训练模型之际,相邻层级过滤器间的相关性。其指出过滤器分组的成效为,于通道维度学习块对角结构的稀疏性,在网络里,具备高相关性的过滤器是借助过滤器分组以一种更具结构化的形式学习得来,从效果层面而言,不必学习的过滤器关系便不再被参数化。能够如此显著地削减网络里头的参数数量,这会致使其不容易出现过拟合的情况,所以,一种相似于正则化的效果浮现出来,使得优化器能够学习收获更加精准更加高效的深度网络。

AlexNet conv1过滤器进行分解,作者指明,过滤器分组好像能将学习到的滤器依据结构把它构组成不同的两组。本图来源于AlexNet的论文,如此而言。句首和句末都各带一个完整短句用于间隔使这种叙述口吻和正式风格更加明显 使其更符合学术论文的表述习惯。
除此之外,每一个进行过滤操作的分组都会去学习数据所呈现出的一种独一无二的表征。就如同 AlexNet 的创作者所指明的那般,用于过滤的分组看上去好像会把所学习到的过滤器依据结构有层次地组织成为两个不一样的分组,一个是针对黑白的过滤器组,另一个是针对彩色的过滤器组。
你认为深度学习领域的卷积还有那些值得注意的地方?