谈谈卷积及其在振动、中心极限定理和更新理论中的应用

卷积的来龙去脉相当复杂，部分人认为它与傅里叶分析联系紧密，然而二者究竟如何相互作用？卷积的根本特性究竟为何？此处从数学视角揭示卷积的非凡作用力。

要明白卷积的内涵，必须先明白傅里叶分析究竟讲什么，它的根本问题是什么，傅里叶级数众所周知，无需多言，但你对傅里叶级数掌握到什么地步，如果你只懂得微积分里那些基础概念，大概连傅里叶级数的皮都没碰到，你只是了解了傅里叶级数的基本定义而已。

要透彻认识傅里叶级数，需要掌握实变函数知识，因为傅里叶分析里，一个核心且关键的问题是，傅里叶级数能否收束？以何种形态收束？

这个议题在微积分领域难以厘清，事实上，即便函数具备连续性，其对应的傅里叶级数也可能在特定位置出现发散现象，我们甚至能够设计出Riemann可积的函数，这类函数的傅里叶级数在所有点都呈现发散状态，倘若你费尽心力将某个函数转化为傅里叶级数，最终却得知其无法收敛，内心必定会感到十分沮丧。差不多像是从没有安装电梯的二十层楼道小跑着下来，结果发现没带汽车钥匙。众所周知开元ky888棋牌官方版，Riemann可积函数是一种特性相当优良的函数，它几乎在积分区间上处处连续，但这究竟意味着什么？微积分学无法解释清楚，若想了解，就必须认真研习实变函数论。即便如此优秀的函数，也无法确保其傅里叶级数必然收敛，由此可以看出问题的严重程度有多深。傅里叶分析是一门历史悠久的学科，其中不少难题在上个世纪中期仍是众人探讨的焦点，由于该领域中诸多悬而未决的议题，人们开始探索新的途径，这恰好是泛函分析发展初期的一个动因。

拖延了大半天，究竟要表达什么意思？稍微冷静些，要是连点耐心都没有，又怎能继续说明白？先从收敛性话题讲起，设想f是一个周期为2π的可积函数（具体周期值并非关键），它的傅里叶级数展开形式如下：

也可以写成指数形式：

其中，

我写不出积分的起止点，反正你们都清楚这是个从零到二π的积分范围，眼下要解决的是如何判定右侧的级数是收敛的。

明白这是什么概念吗？这就是序列的部分总和，我们的目的是把它表示出来，从而判断这个总和是否趋于极限，想要求出这个序列的总和是白费力气，你若能成功，天下就是你的，不过，我们可以把系数的积分形式引入序列，由此得到：

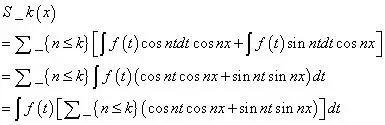
还清楚三角函数公式吗？明白方括号中的和如何计算吗？倘若不清楚，仍有机会，可以借助指数形式的级数再试一试。

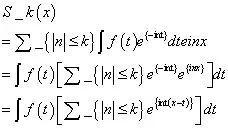
最终，这个求和能否完成？倘若依旧无法解决，你仅存一次机会开yunapp体育官网入口下载手机版，需用你的智慧狠狠撞击南墙十二回，或许能唤醒你学生时代的美好回忆。

明白为什么要定义卷积了吗？

当前任务转变为判定前述积分是否趋向于f(x)，情形看似明了，可惜未必如此，前述积分未必能趋向于f(x)！究竟何种函数的傅里叶级数会收敛？以何种形态收敛？此疑问暂且搁置，毕竟许多场合不要求收敛即可，若要详尽阐释，则需超越常规微积分的界限。那么开yun体育官网入口登录app，面对傅里叶级数不收敛的函数，难道我们就束手无策了吗？人类毕竟非常聪明，总能找到解决之道，S_k(x)无法收敛，不妨研究一下部分和的中值，这个尝试带来了惊喜，这些部分和的算术中值竟然几乎在所有地方都趋于稳定！这个算术中值究竟是什么？我们接着进行计算。

将D_k(x ) 带入可以算出

于是

我们再次获得了一种卷积，Fejer 定理揭示，那个积分在几乎所有点上趋于 f(x)。

D_k有另一个名字，叫做Dirichlet核，而F_m则被称为Fejer核，他们之间的卷积运算，也被称作带核的积分运算。事情并没有就此告一段落，恰恰相反，这仅仅是一个崭新的起点，一个具有深远影响的积分算子理论，由此正式拉开序幕。