数学第一家族和“伯努利方程”
引语
流体行为诡谲莫测
比描述黑洞还要难
1912年秋季,名为“奥林匹克”的大型海轮于广阔海域中行进,在距离这艘全球最大远洋船舶120米远的地方,有一艘体量相对较小的巡洋舰“豪克”,该舰船长目睹这艘世界级巨轮时感到十分激动,于是驾驶“豪克”号高速追上,并保持与“奥林匹克”同向并行的姿态,内心怀揣着“无论多么庞大的船舶,我都有能力与之比肩而驰”的信念。
世事难料,航行中的“豪克”忽然被“奥林匹克”所牵制,舵手无法挽回航向,直直撞向那艘巨轮,最终导致一场骇人听闻的海上灾难。
这次海上的意外事件,使警方完全束手无策,由于无人知晓,造成这起灾难的真正原因是流体力学里的“伯努利方程”。
提及“伯努利方程”,需提及一个历史悠久的数学流派,该流派的玄妙与难以捉摸,堪比流体运动的特性。
伯努利家族:数学第一世家
伯努利家族堪称科学史上的一个异数,其成因令人费解,究竟是什么因素促成了这个家族的辉煌。
这个家族过去曾有过十多位数学家,他们中间有的担任过欧拉的导师,有的与莱布尼茨交好。即便不讨论纯理论数学,这个家族在工程、技术等方面同样人才辈出,在法律、管理、文学、艺术等领域也成就斐然,仅被后人记载过的杰出人物就达到120位,堪称科学界的翘楚,数理领域的名门正派。
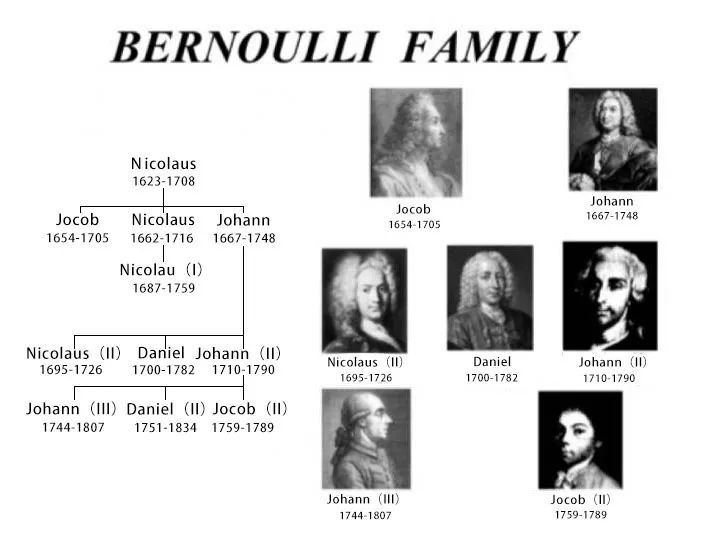
在18世纪期间,更涌现出雅各布·伯努利、约翰·伯努利以及丹尼尔·伯努利三位顶尖的全球性数学家,他们一致在微积分的进步和运用上担当着继往开来的主导职责,促进了全人类科学领域的成长。
雅各布·伯努利是这个家族中最早一位反叛者,他舍弃了伯努利家族传承下来的商业财富,毅然决然投身于数学研究之中,从此一发不可收拾。这位让父亲极为失望的长子,成功证明了被称为大数定律的重要定理,是概率论领域的开拓者之一,同时也解决了一系列早期的微积分难题。微积分领域的共同缔造者牛顿毕生最大的对手莱布尼茨,曾感叹除了自己之外,世间再无人能像雅各布那样精通微积分的奥秘。雅各布留下最著名的一句话是:我违父意,钻研群星。
约翰·伯努利是雅各布·伯努利的弟弟,哥哥的性情乖张给约翰造成很大困扰,老尼古拉把家族荣誉的重担放在约翰身上,约翰很聪明,为了学习数学,最终以攻读医学为借口进入大学,和莱布尼茨关系非常好。他成为变分学说的开创者,1696年通过公开渠道揭示了知名的“寻求最短路径难题”,还教导了欧拉、克莱姆、洛必塔、丹尼尔、尼古拉二世等诸多才华横溢的数学家。
丹尼尔·伯努利是一位物理学家、数学家兼医学家。他是约翰·伯努利的儿子,堪称伯努利家族中学识渊博的典范,也是家族里成就最为卓著的人物。他撰写的数学和力学著作、论文数量超过八十篇,是数学物理方法的重要奠基者。1738年,他出版了《流体动力学》一书,从而登上了科学的高峰,被誉为流体力学的开创者,后世尊称他为“流体力学之父”。
“流体漩涡”中的家族纷争
科学的光芒异常耀眼,与此同时,数学领域这个大家族内部的矛盾却持续不断。
这个家族舍弃了凡间的钱财,却把对数学成就的渴望,变成了另一种灾祸。
雅各布·伯努利与弟弟约翰·伯努利之间存在矛盾,两人在对“双曲余弦函数”“降速曲线”进行论证时彼此诘难,最终形成了毕生的竞争关系。
雅各布在生命终结前开元棋官方正版下载,依然不忘中伤自己的兄弟,声称倘若自己不久于人世,那弟弟必定会重返巴塞尔,他绝不会考虑任何别的职位,唯一的心愿便是继承自己的位置。
兄弟反目更为恐怖,约翰·伯努利和丹尼尔·伯努利父子间,也发生过激烈的争斗。
1734年,丹尼尔·伯努利带着巴黎科学院的大奖回到故乡,父亲约翰当即作出决定,要将儿子逐出家门,他无法容忍儿子日益显露的数学才华可能威胁到自己的学术地位,这种嫉妒心理,或许比年轻时想要击败哥哥雅各布时更为强烈。
约翰·伯努利曾在私人笔记中狂妄地记录:“与我竞争的人都先我离世,并且他们年纪都比我小,这实属天意。”他独自屹立于巅峰,即便孑然一身,也不容许任何人遮蔽他的光辉,包括自己的儿子在内。
数学如同套在约翰·伯努利指尖的神秘饰物,他渴望独自完全掌控,不允许任何人触碰分毫。
丹尼尔有意避开父亲钻研的范畴,转而钻研流体力学学问,尽量减少同父亲熟悉的范畴接触。可是约翰却对丹尼尔钻研的范畴非常着迷,在丹尼尔出版著作《流体力学》之后,他紧接着出版了一本《水力学》,并且特意将写成时间标明为1732年,想要证明自己的优先权。然而没过多久,约翰的手段就被拆穿,因为丹尼尔写书时始终与别的学者沟通,约翰这本书的突然出现实在令人意外。更糟糕的是,约翰实际上从儿子的著作里窃取了内容,偷走了儿子的学术成果。
伯努利方程:弧线的魅力
《流体力学》究竟具有什么魔力,使得父亲不惜抄袭儿子的成果?
伯努利方程究竟有何卓越之处,丹尼尔竟能凭借此方程,在家族内部以及科学领域声名鹊起,大获成功?
1726年,丹尼尔注意到日常中一个微小的异常情况,即开启水龙头后,涌出的水束宽度小于水龙头本身的开口。他发现,脱离水龙头的水流所承受的力,要少于其周边的静止空气所产生的压力。因此,水流会收缩成更狭窄的水柱形态,其直径明显小于水龙头出口的尺寸。
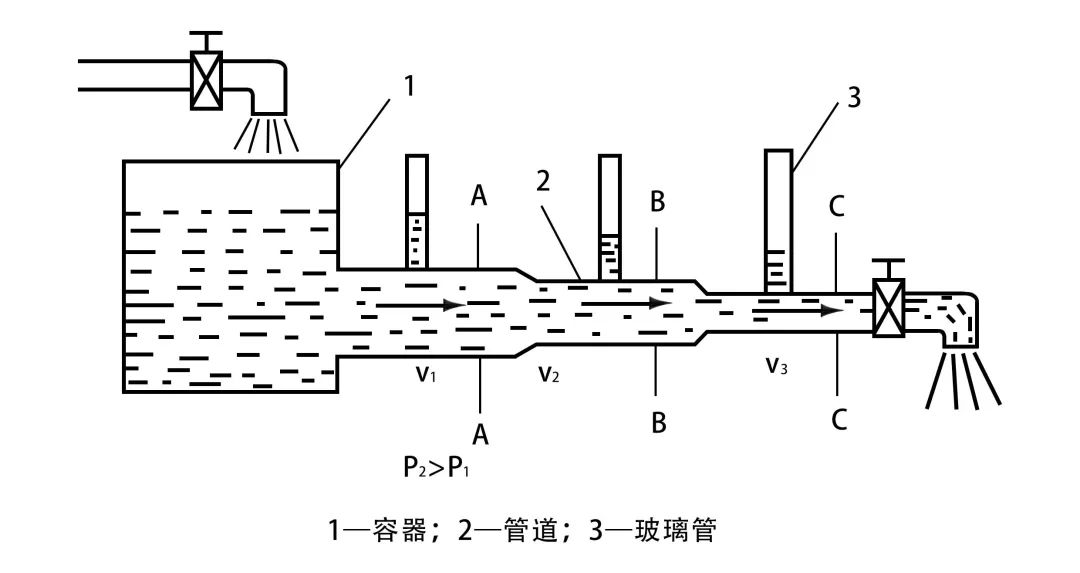
丹尼尔试图证明自己的想法,他多次进行实验,将水引入一个平放着的玻璃管,玻璃管是透明的,然后在玻璃管上直直地插进一根同样透明的细管,通过看细管里水位如何变动,就能知道水流承受的力有多大。如果水流产生的压力比较大,细管里的水位就会升得比较明显,要是压力小,水位就会往下掉。果然预料之中,伯努利察觉到,水平管里水流速率变大,垂直管里压力就会降低,并且降低幅度同水流速率的平方值成正相关。因此,流动的水体比静止的水体压力要小,并且流速越快,压力就越小。
这一推断即为后来著名的“伯努利原理”。
1738年,丹尼尔在其著作《流体力学》里,运用伯努利原理,提出了另一种数学形式,即“伯努利方程”,这一表述与原理论具有相同含义。
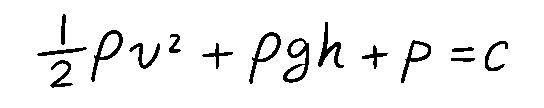
p,代表流体中某点的压强
ν,代表该流体中某点的流速
g,为重力加速度
h,该流体中某点所在的高度
ρ,为流体密度
c,为常数
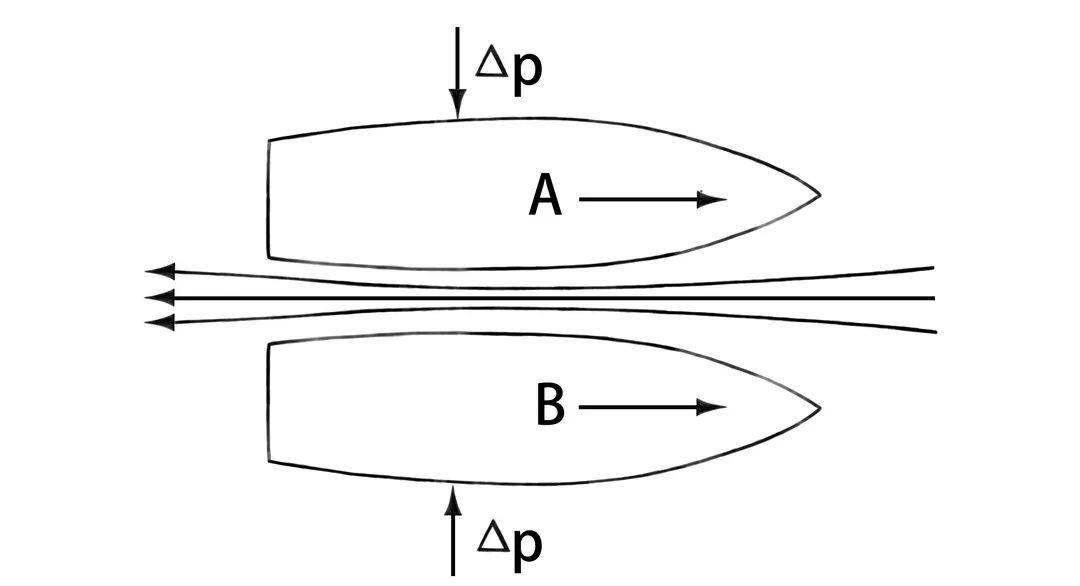
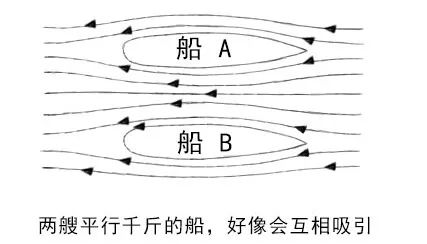
在此,需要说明的是“奥林匹克”号客轮为何会撞上“豪克”号。
两艘船只头相向,中间水域相对狭窄,水流速度比船体两侧快,水压则较低,而船外两侧的水流速度较慢,水压较高。因此,两侧高压力的水会推着船只向中间靠拢,最终导致船只相撞。
伯努利家族延伸线:流体无限
约翰晚年曾与儿子丹尼尔激烈冲突,不过当丹尼尔还年轻的时候,他是一位称职的父亲。
1725年,丹尼尔在彼得堡科学院任职,担任生理学院士和数学院士,其父约翰对此感到担忧,认为儿子难以胜任这一职位,于是指派了自己的得意弟子欧拉,也就是数学史上的杰出人物,前往协助丹尼尔工作。
跟随太子求学期间,欧拉并未遭受任何损失,他在这个数学世家收获了诸多益处,他借助丹尼尔·伯努利创立的无穷插值技巧,出色地推导出阶乘函数在全体实数上的公式——也就是伽玛函数。当他遇到伯努利方程时同样欣喜若狂,但丹尼尔所给的方程过于简单明了,完全无法彰显数学顶级家族的学术风范再说伯努利家族向来以精于微积分著称,欧拉作为得力助手,却擅自将伯努利方程发展为新版伯努利方程。
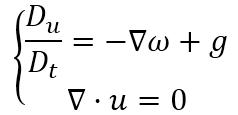
再参照一下伯努利定律,是不是有种立刻领悟了研究生阶段知识的体会。那个时期欧拉年仅二十岁,确实是知名数学家兼教师约翰.伯努利的门生,他将动量守恒和质量守恒引入到流体动力学领域,创立了理想流体的通用公式开yunapp体育官网入口下载手机版,尽管后来流体力学领域人才济济,杰出数学家数不胜数,但这两大守恒定律却无人敢违背……
但是,丹尼尔内心的真实想法我们无从了解,虽然他作为欧拉毕生的朋友,一方面是暗自高兴,另一方面却认为这是炫耀。
在伯努利家族中,柯西·约翰是继欧拉之后的第三代传人,他担任过欧拉的导师,而欧拉则对拉格朗日产生了深远影响,拉格朗日又成为了柯西的良师益友。
柯西希望彰显自己在数学界的地位,他在伯努利方程2.0的基础上推出了伯努利方程3.0,即柯西动量定理,这是一个涉及九维张量的方程式。
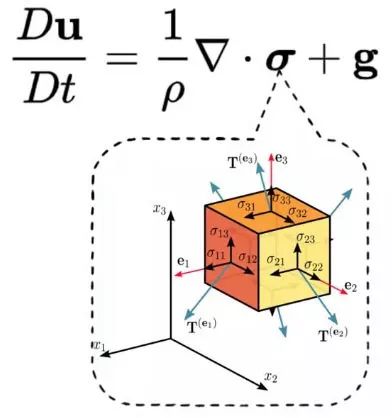
σ为张量
空间维度瞬间从三个力场变为九个力场,柯西在欧拉的三维力场基础上,立刻补充了六个剪切力场。水准有所提升,却让众多原本打算钻研流体动力学的同好望而却步,剩下的人几乎只能对着公式发愣,直到一个世纪之后纳维和斯托克斯揭示出“粘度乘以速度的散度”能够导出剪切应力,这两位勇于探索的数学家共同创立了纳维-斯托克斯方程(简称N-S方程),学术界才重新开始严肃审视流体力学公式,这种审视持续了一百五十五年。
伯努利方程4.0:纳维-斯托克斯方程
2000年前后,美国克雷数学研究所挑选了七个数学难题,设立了总额达七百万美元的奖金项目。
这七个“世界性难题”包括:NP完全问题、霍奇猜想、庞加莱猜想、黎曼假设、杨-米尔斯存在性与质量缺失、N-S方程、BSD猜想,它们均获得了一百万美元的悬赏。
如今,距离1845年系统阐述“伯努利方程4.0(N-S方程)”已历经155载光阴,要解算这个非线性偏微分式,不知多少杰出人物为之倾倒,就连纳维和斯托克斯面对它也束手无策,N-S方程求解极为棘手,仅在极少数简单流动情形下才可能获得精确答案。例如把N-S方程沿流线积分可得到粘性流体的伯努利方程:
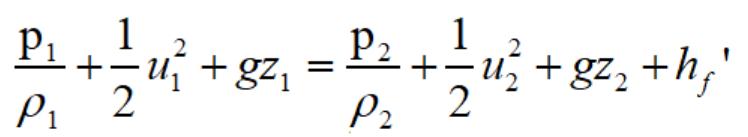
N-S方程的计算极为复杂,但流体力学意义非凡,人类活动无处不在,水流与气流也无处不在,必须进行探索。航天器运行依赖流体力学,水下航行器运行依赖流体力学,港珠澳大桥建设依赖流体力学,南水北调项目依赖流体力学,找到一种精确的计算方法,是所有科研人员的追求。
不要以为推算黑洞的史瓦西解有多复杂,真正需要高超技巧的是测算小区里那棵老苹果树上落下的叶片的运行路线。
就这样,很多人算啊算啊算,就是想拿下这一世纪难题。
总结下来,求解流体的精确解主要分为两大流派。
首个流派属于理论学界,该领域以杰出学者为核心,这些学者普遍自视甚高,坚信仅凭卓越才智便能发现普适性法则,无需受制于伯努利家族的学说,代表人物有麦克斯韦、玻尔兹曼等,他们分别致力于探索微观层面的规律开yun体育app入口登录,进而揭示宏观世界的运行模式,并试图解开流体行为中难以预料的奥秘。
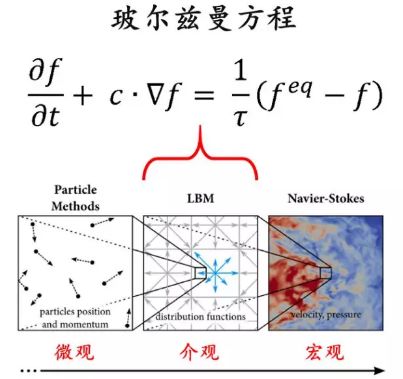
第二种取向属于实证主义。该派别的研究者全是实证主义学者,他们坚信伯努利原理是应对各类挑战的根本依据,不采信那些虚无缥缈的主观臆断,而是致力于通过一系列具体探究来构建数学框架求解,针对不同性质的流体选用相应的计算模型,认为世间没有哪个难题是实验无法攻克的,倘若遇到瓶颈,那就设计新的实验方案继续攻关。该流派中最具代表性的研究者有如下几位:
雷诺实验。将瞬间速度分解成随时间统计平均速度和脉动速度。
RANS模型。假定涡流带有粘滞特性,并且设九维张量等于涡流粘滞度与流体形变程度的乘积。
涡粘模型,采用涡粘性系数,用以表现湍流流动,借助涡粘度,将雷诺应力,与平均流场,关联起来。
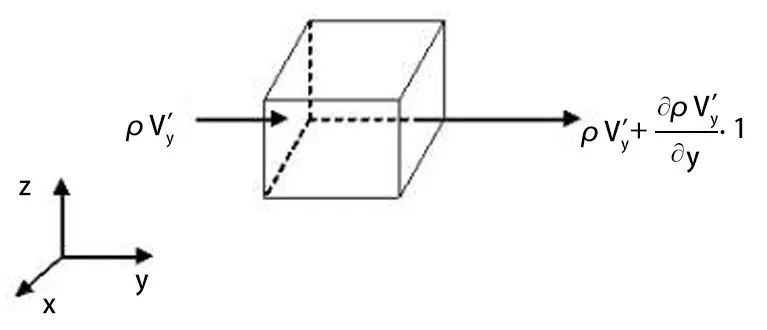
纳维-斯托克斯方程继承了伯努利方程的卓越成就,这个深奥的数学分支,我们至今仍未完全解开它的秘密。
结语
我们会有这样的数学世家吗?
多年过去,谈起伯努利家族之余,众人依旧嘘唏。
这个家族舍弃了商场上的喧嚣,把全部心血投入到冷静的数理之中,他们赢得了学术领域的极高成就,却承受了家庭内部的激烈冲突,兄弟间产生嫌隙,父子之间也出现隔阂。
这到底是一个被上天眷顾的家庭,还是一个受到智慧诅咒的族类?
伯努利家族在学术上承袭了惠更斯与莱布尼兹的衣钵,引领欧洲大陆开展以约束运动和能量守恒为核心的力学探索,为后续分析力学的诞生奠定了根基。这同样为后来以法国、俄罗斯及德国为焦点的欧洲大陆学术流派的发展提供了支撑。其中,“伯努利方程”无疑是其最为杰出的贡献之一。
那个群星璀璨、精英辈出的伯努利家族现象,数百年间持续吸引着世人的目光,它揭示了一个道理:家族的“近墨者黑”,往往能成为天才孕育的沃土,未来我国是否也会诞生类似的数学门庭呢?
参考资料:
邹立尧, 陈世元等人, 进行了关于电动汽车辅助电源的研究, 该研究基于伯努利原理, 发表于《微电机》期刊, 时间是2013年
陈昱澍的文章《冤屈的船长——谈伯努利原理》发表在《中学物理》上,时间是在2003年
黄桦,陈小敏,通过《物理教学》期刊,阐述了教科书中伯努利原理演示实验存在的错误,并提供了正确的解释,该研究发表于2017年
L.朗特的作品《流体力学基础》,由郭永怀和陆士嘉负责翻译工作,该著作于1981年出版,出版社是科学出版社,出版地点位于北京。
王运东,骆广生,刘谦所著书籍名为《传递过程原理》,由清华大学出版社于2002年出版发行。
孤独求静,流体力学野史,2019


